|
|
|
|
|
|
|
|
https://zhuanlan.zhihu.com/p/166635438?ivk_sa=1024320u
|
|
|
|
|
|
## 格点作图问题的技巧(一)
|
|
|
本文不讲那些平移旋转轴对称的格点作图题,因为那太简单,且所有关键点都在格点上,没有意思。
|
|
|
|
|
|
我最近通关了一款游戏叫《Pythagorea》,游戏的内容就是在格点上作图来达成目标,下面的一些例题出自里面的关卡,据我了解,目前好像只有天津的中考有考这类问题。
|
|
|
|
|
|
本文要介绍的内容:
|
|
|
|
|
|
平行线的做法
|
|
|
|
|
|
垂线
|
|
|
|
|
|
做轴对称点
|
|
|
|
|
|
垂直平分线
|
|
|
|
|
|
角平分线
|
|
|
|
|
|
#### 作图工具:无刻度的直尺
|
|
|
**一,平行线的做法**
|
|
|
|
|
|
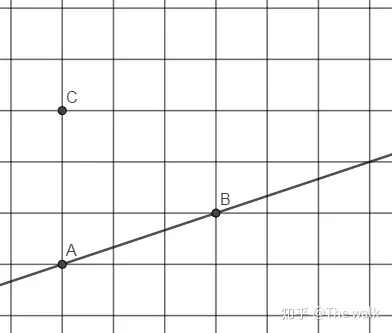
1)A,B,C是格点,求作C关于A,B的平行线。
|
|
|
|
|
|
|
|
|
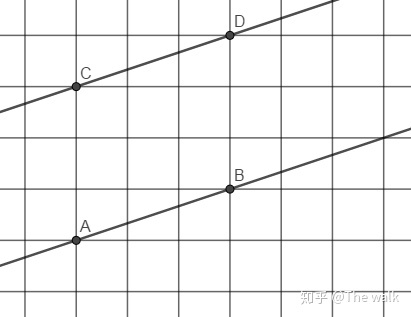
非常简单,做法:
|
|
|
|
|
|
其实很简单吧,看一眼就会做。
|
|
|
|
|
|
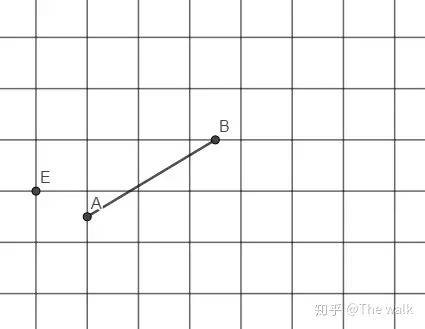
2)A,B是边中点,过E点作关于AB的平行线
|
|
|
|
|
|
|
|
|
做法1:硬做
|
|
|
|
|
|
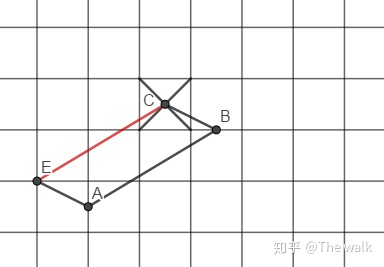
取C点,C点是正方形中心,CE为所求
|
|
|
|
|
|
> **黄海解读**:EC可以理解为AB向左移一位,上移0.5位的结果
|
|
|
|
|
|
这个做法很显然是直接将AB平移至E得到的,实际操作过程中只要做出C点就行了,不必连接AB,AE。
|
|
|
|
|
|
做法2:A字相似
|
|
|
|
|
|
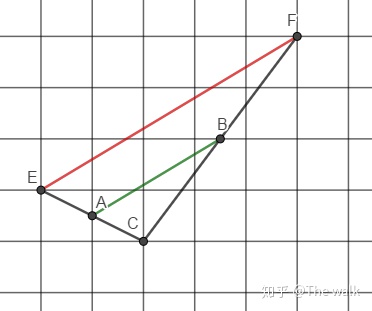
延长EA至C,使得EA=AC(下面简称“延长X倍”)
|
|
|
|
|
|
|
|
|
|
|
|
可知C点是格点,延长CB一倍到F,可知F点是格点,易得$\triangle ACB \sim \triangle ECF$,易得EF//AB,EF所求。
|
|
|
|
|
|
事实上,如果将EA延长n倍至点C,那么CB也要延长n倍至点F,这要根据情况看那个方便。
|
|
|
|
|
|
**3)需要注意的一点是,注意网格的大小,不要超出网格范围,比如下面这题**
|
|
|
|
|
|
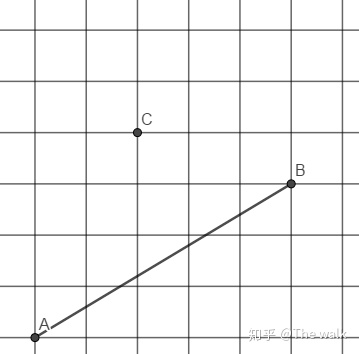
A,B,C是格点,求作C关于AB的平行线(网格大小只有截图这么大)
|
|
|
|
|
|
|
|
|
|
|
|
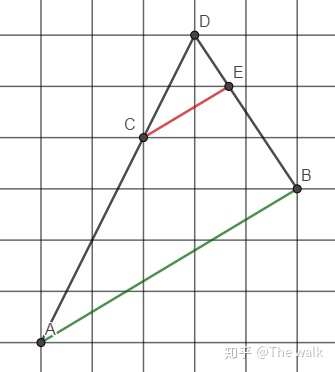
做法1,延长AC到D,D是格点,易得AD:CD=3:1,连接DB
|
|
|
|
|
|
|
|
|
取DB与网格线的交点E,易得BD:DE=3:1,得相似,推出$CE//AB$,CE所求。
|
|
|
|
|
|
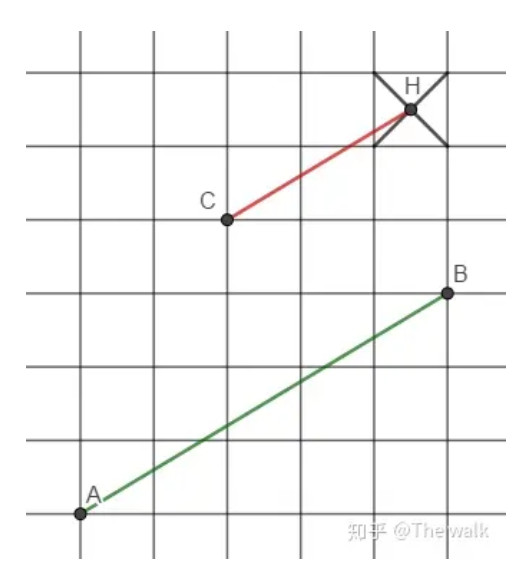
做法2,硬作
|
|
|
|
|
|
|
|
|
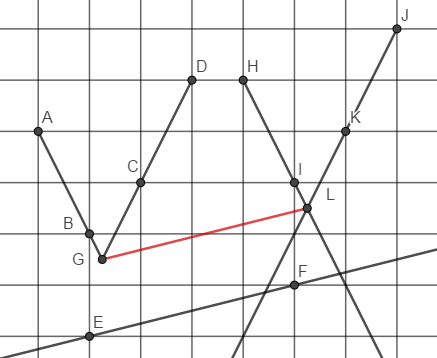
4)G是AB与DC的交点,求作G关于EF的平行线(格点不再说明) |