2.0 KiB
1、
S_深=40*30=1200平方米
S_浅=8*30=240平方米
放水速度
(2592-1152)/2.5=576 (m^3/h)
2、Q=kt+b
将特殊点代入
t=0,Q=2592
t=4.5,Q=0 求解出k和b即可
b=2592,k=-2592/4.5=-576
所以方程:Q=-576t+2592
t的取值范围就是0<=t<=4.5
3、进水时,先是需要浅水、深水一起覆盖,待浅水区满了后,再单独覆盖掉深水。
题目要求的是水深与时间的关系式,根据上面的分析,应该是两段,第一段是两个一起来,后面是深的单独来,所以可以知道,最初的是一条斜率较小的直线,后面是一条斜率较大的直线,是一个分段函数。
因为要计算出水深,需要知道的条件是深水区、浅水区的深度分别是多少,才能知道分段函数的分界点在哪里。
根据现有条件,推算出两个水区的深度:
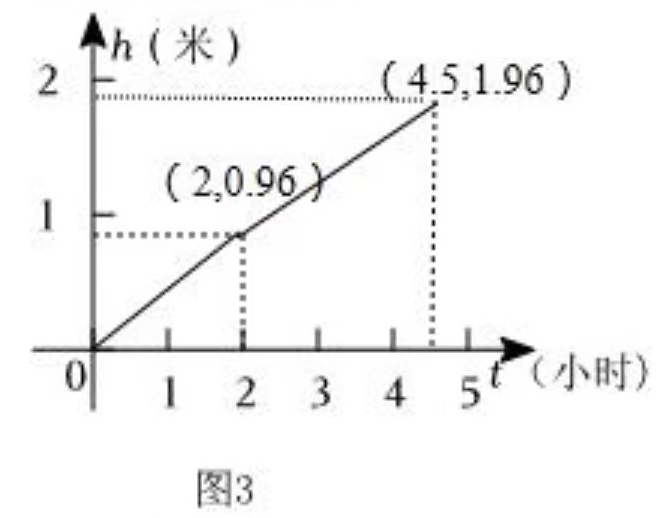
观察图2,找出它的分界点,也就是P点。
在直线1152处,说明此时浅水区放光了,剩下要放深水区,那么2592-1152就是深水、浅水一起放,浅水区放光时的总水量。我们同时还知道深水、浅水的面积,总水量除以面积,就是体积除以面积,得到的就是高度,此时的高度也就是浅水区的高度了:
(2592-1152)/((40+8)*30)=1米
下面来求深水区的深度:
(1152/1200)+1=1.96米
进水时,水的速度为576m^3/h,在第一阶段,水需要覆盖掉深水区,体积就是
- 深度
1.96-1=0.96m - 面积
1200m^2 - 体积=
0.96*1200=1152m^3
t=(1152m^3)/(576m^3/h)=2小时
也就是说,在前两个小时,需要覆盖掉深水区比浅水区深的那部分。
h=576t/1200,即h=0.48t ,此时0<=t<=2
因为进水出水都是一件事的两种走法,所以最终的时长一定也是4.5小时,后面的时间范围2<t<=4.5
h=0.96+\frac{576}{1440}(t-2)
\therefore h=0.4t+0.16