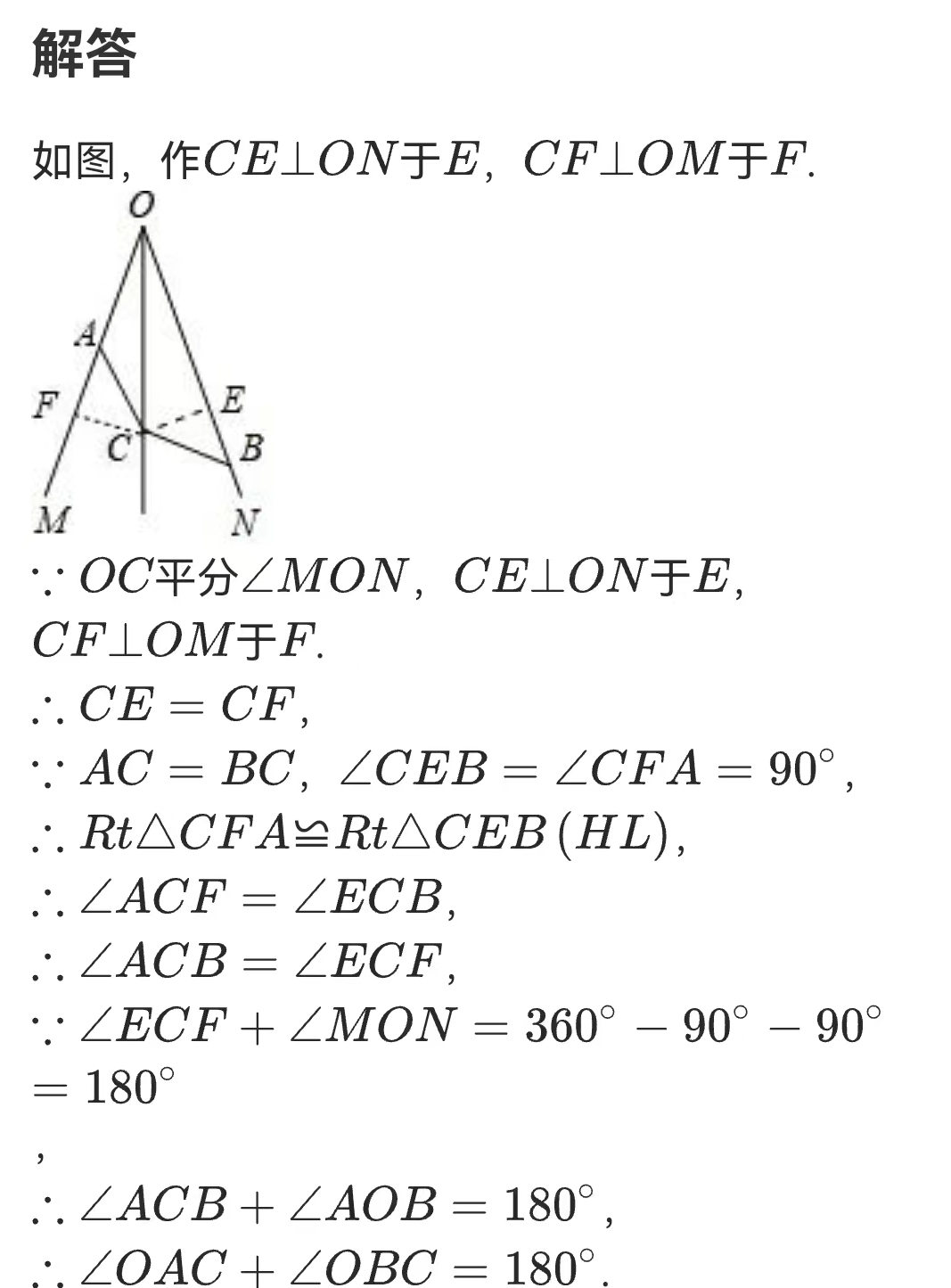
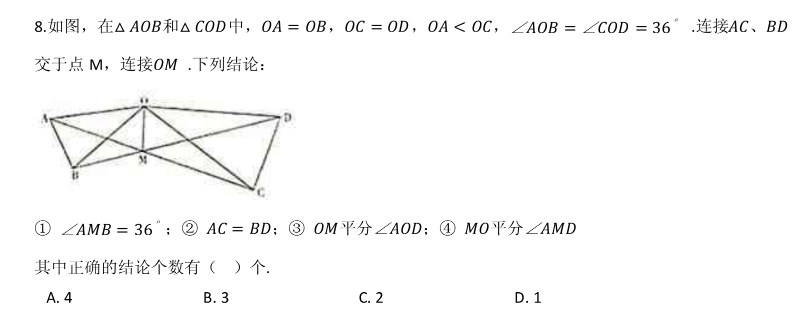19 KiB
一、前导知识
1、三角形全等判定定理
1.三组对应边分别相等的两个三角形全等(简称SSS或“边边边”),这一条也说明了三角形具有稳定性的原因。
2.有两边及其夹角对应相等的两个三角形全等(SAS或 “边角边”)。
3.有两角及其夹边对应相等的两个三角形全等(ASA或 “角边角”)。
4.有两角及其一角的对边对应相等的两个三角形全等(AAS或 “角角边”)。
5.直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(HL或“斜边,直角边”)。
SSS,SAS,ASA,AAS,HL均为判定三角形全等的定理。
注意:在全等的判定中,没有AAA(角角角)和SSA(边边角)(特例:直角三角形为HL,属于SSA),这两种情况都不能唯一确定三角形的形状。
Tips
两个角相加等于 90^ \circ ,叫互余;两个角相加等于 180^ \circ,叫互补
2、垂直平分线
1、线段的垂直平分线(中垂线)
(1)定义:经过线段的中点并且垂直于这条线段的直线,叫做线段的垂直平分线。
(2)性质:线段垂直平分线上的点到线段两个端点的距离相等。
(3)判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
(4)画法:线段AB的垂直平分线,分别以线段AB两个端点为圆心,大于AB长为半径画弧,两弧交于两点CD,则直线CD是线段AB的垂直平分线。
2、轴对称
(1)轴对称图形:如果一个图形沿着某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形。这条直线叫做对称轴。
(2)轴对称:把一个图形沿着某一条直线折叠,如果能够与另一个图形完全重合,就是说这两个图形关于这条直线对称,这条直线是对称轴,折叠后重合的点是对应点,叫做对称点
(3)性质:
①关于某条直线对称的两个图形是全等形
②如果两个图形关于某条子线对称,那么对称轴是任何一对对应点所连接线段的垂直平分线;
③两个图形关于某一条直线对称,如果它们的对应线段或者延长线相交,那么交点在对称轴上。注:轴对称图形一定是全等形,全等的图形不一定成轴对称。
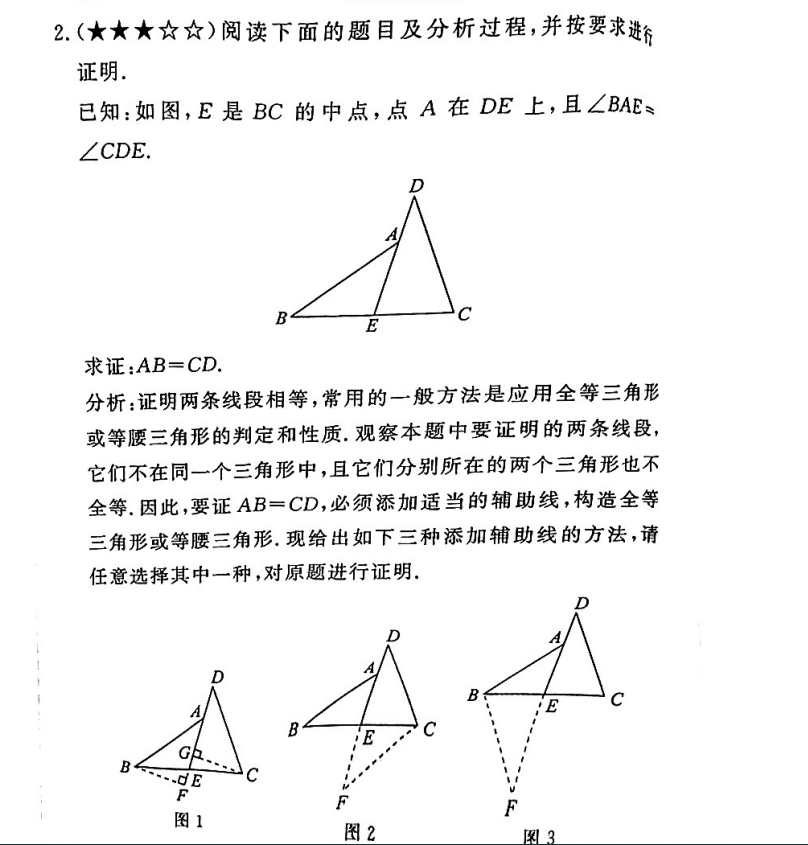
二、练习题
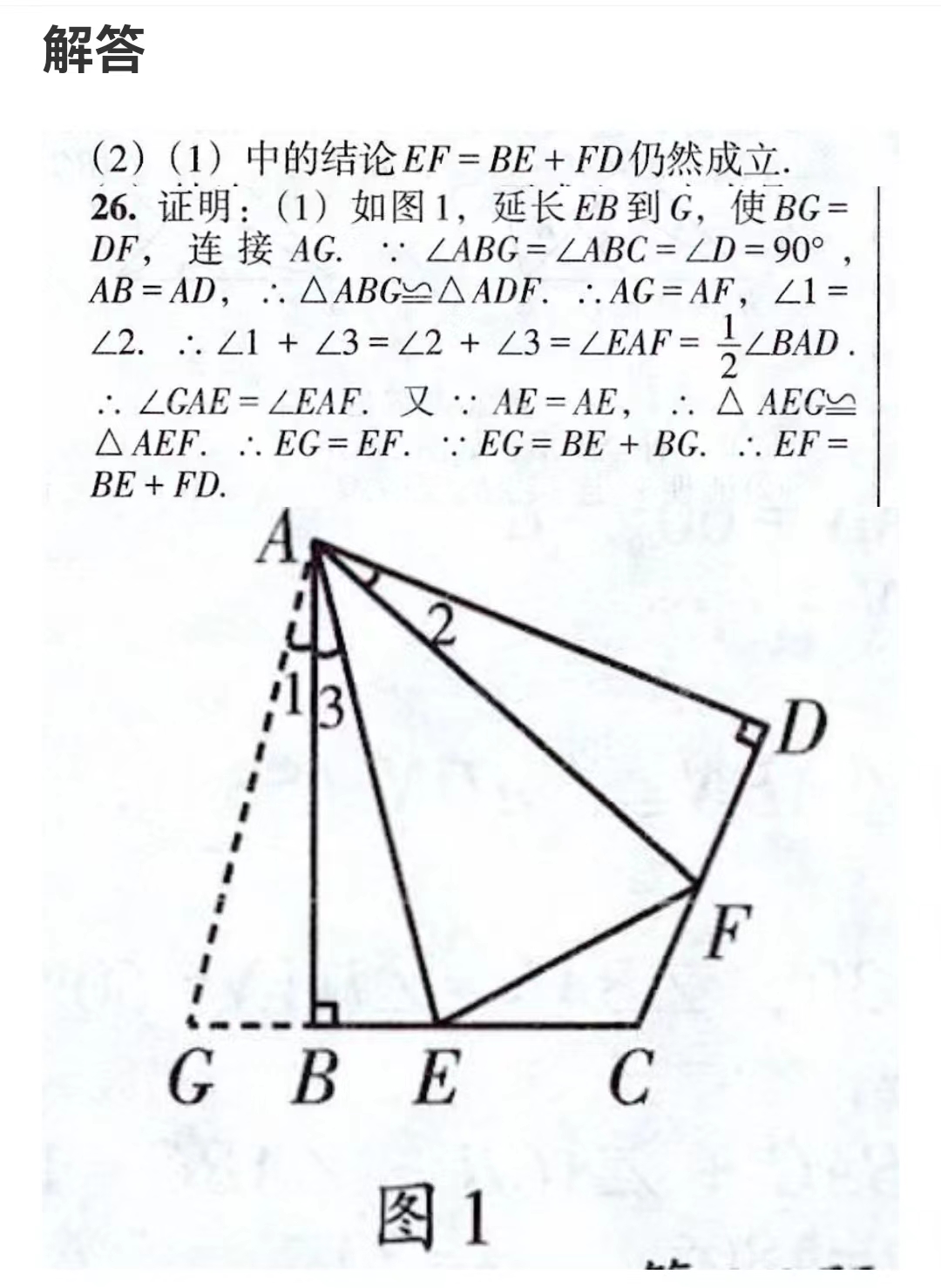
思路:
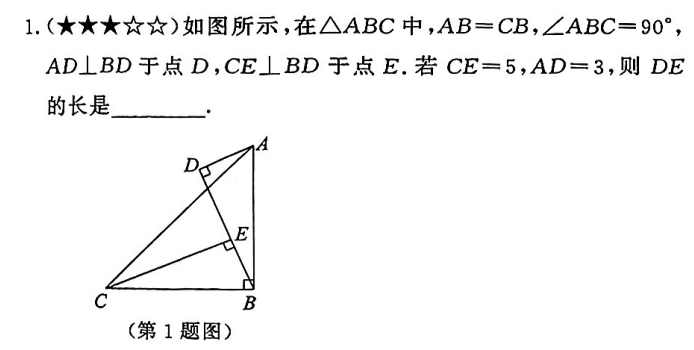
- 因题目告之
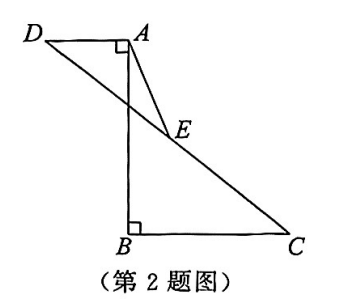
AB=CB,同时\angle ABC=90^ \circ,所以是一个等腰直角三角形。 \angle CBE + \angle DBA= \angle DBA+ \angle DAB\therefore\angle CBE = \angle DAB- 又
\because BC=AB
根据直角三角形判断相等 AAS,
\therefore \triangle CEB \cong \triangle ADB
\therefore EB=AD=3,DE=DB-EB=CE-DB=5-3=2
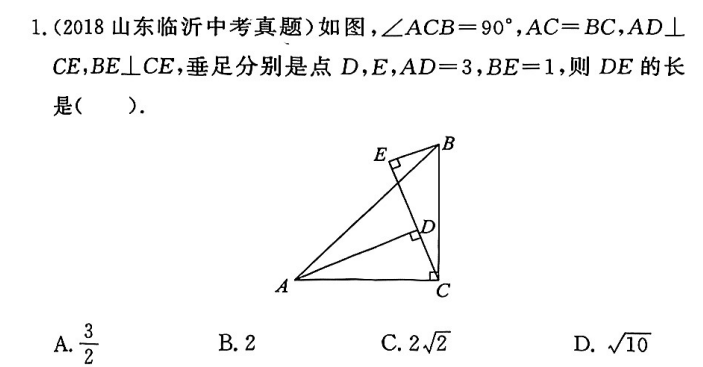
 解:
解:\triangle CEB \cong \triangle CDA 即可,SAS
 解:
解:\triangle BDA \cong \triangle ACE \therefore \angle 3= 55^ \circ
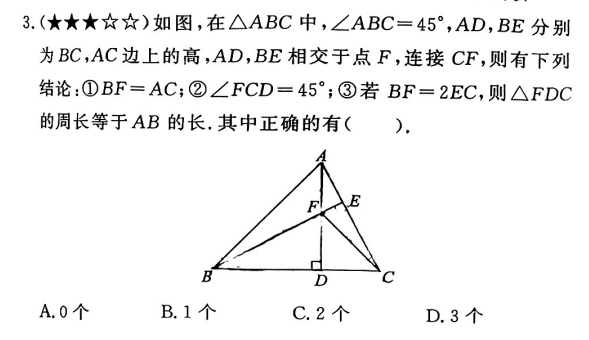
解:
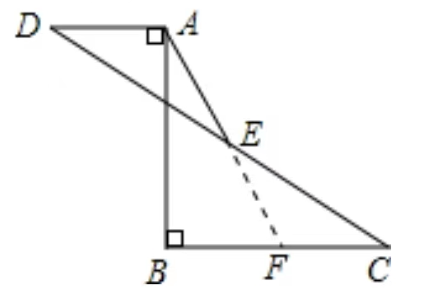
① \because \angle ABC= 45^ \circ
\therefore \triangle ABD 为等腰直角三角形, AB=DB
\therefore \triangle DFB \cong \triangle FDB (AAS)
证毕
②
\because FB=DC \angle ADC= 90^ \circ
\triangle FDC 为等腰直角三角形
\therefore \angle FCD= 45^ \circ
证毕
③ BF=2EC,所以E为中点,BE就是垂直平分线。
\therefore AF=FC,AB=BC(垂直平分线的性质)
\therefore AB=BD+CD=AD+CD=AF+DF+CD=CF+DF+CD
证毕
湖北鄂州 中考真题 初中数学 2020
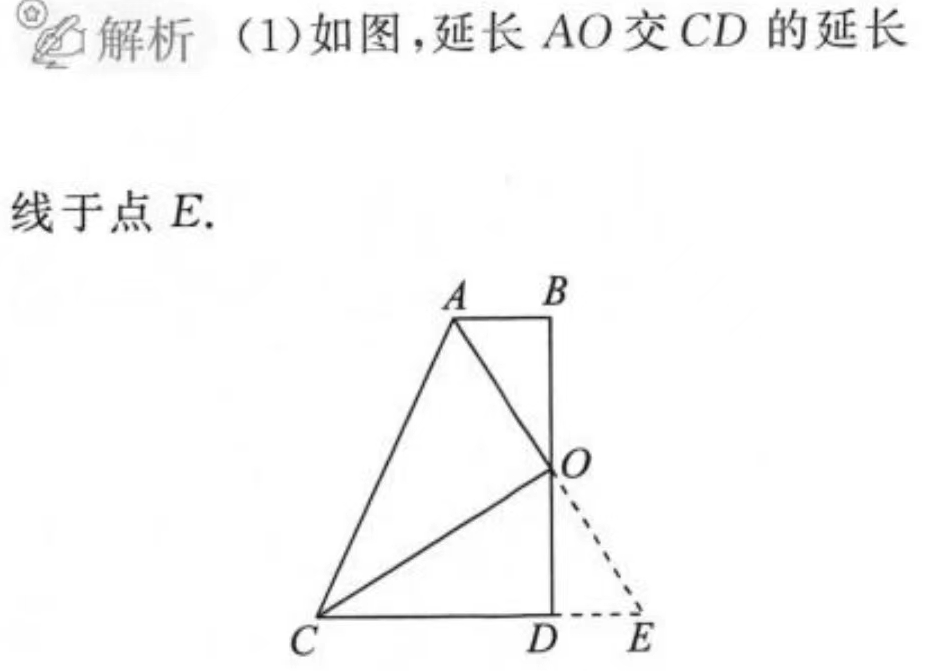
\triangle AOC \cong \triangle BOD
\therefore AC=BD ② ✔
\because \angle AMB= \angle DMC (对顶角)
\angle ACO =\angle ODB
\therefore \angle COD=CMD (两个三角形中,有一个共顶角,另外两个角相等,剩下的两个角也一定相等)
\therefore \angle AMD= \angle COD= 36^ \circ ① ✔
由O向AC,BD引出垂线,垂足为H,G,因为 \triangle AOC \cong \triangle BOD ,所以对应边的垂线长度也一定要等,\triangle OHM 与 \triangle OMG 共用一条边OM,并且,另一条直线边还相等,所以
\triangle OHM \cong \triangle OGM
\therefore \angle AMO =\angle DMO ④ ✔
现在还看一下 ③
反证法:假设 \angle AOM=\angle MOD 看看会不会有矛盾产生。
\large \left\{\begin{matrix}
\angle AOM= \angle MOD & \\
OM=OM & \\
\angle OMA= \angle OMD & (上面的结论 ④)
\end{matrix}\right.
根据ASA定理,则 \triangle AOM \cong \triangle OMD
\therefore OA=OD=OC,而题目明确给出OA<OC,所以假设错误,③ ✘
总结
- 构造直角三角形,利用三角形全等来判断角是不是相等
- 反证法,同时注意读题中的隐含条件,想一想他为什么要给出这样一个条件
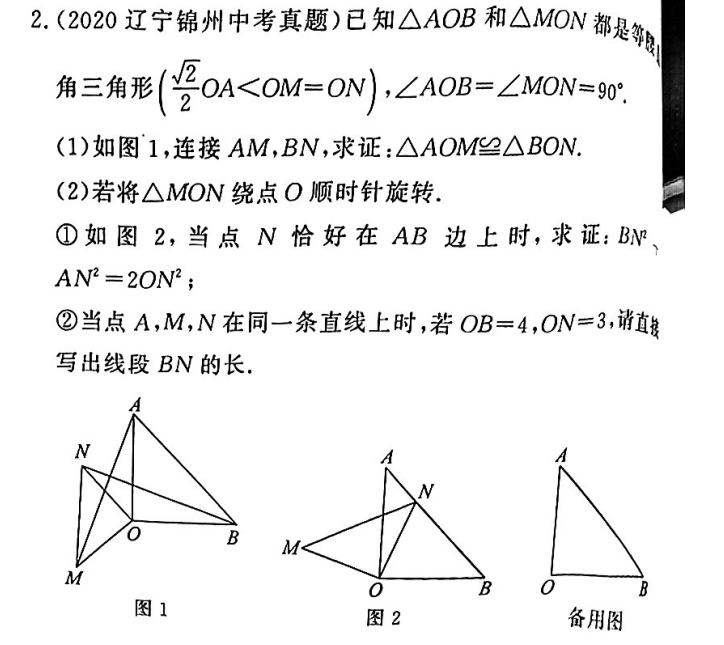
SAS可以证明 (1)
连接A->M,根据结论(1),依然有 \triangle AMO \cong \triangle NOB
\because \angle OAB=45 ^ \circ
\angle MAO=\angle OBA=45 ^ \circ
\therefore \angle MAN=90 ^ \circ
MN=BN
MN^2=AB^2=2ON^2
证毕
前导知识 ####学习平行四边形判定要学好,这五种方法要掌握牢
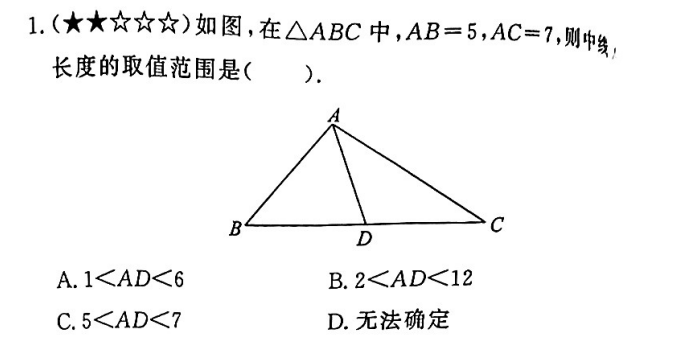
延长AD,截取DE=AD 则D为AE,BC的中点,平行四边形判定办法,知道ABCE为平行四边形。
AE<AB+BE=AB+AC=7+5=12,所以AD<6
同时,AE>AC-CE=7=5=2,所以AD>1
选A
三个都需要仔细思考,并由教师进行点拨
答:
(1) SAS
(2) AB-AC<AE<AB+AC \Rightarrow 2 <AE <10 \Rightarrow 1<AD<5
(3)
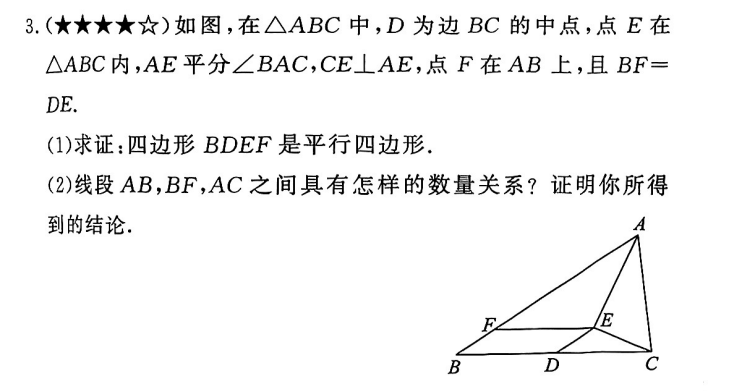
BF与AC不在一个三角形中,不好直接证明,需要引辅助线。- 一般中线的题,都是把中线延长一倍,然后再来思考解决办法。
\triangle BDH \cong \triangle ADC \ SAS
如此,成功的把AC转化为BH,而BH与BF在同一个三角形中,就是证明\triangle BFH是等腰三角形即可,问题得到转化。
\because \triangle BHD=\triangle ADC 平行四边判定办法,内错角相等
在,而\triangle BFH=\triangle AFE,而AE=EF,所以\triangle AFE=\triangle FAC=\triangle BHA
结论:\triangle BHD=\triangle BFH \Rightarrow BF=BH=AC
【前导知识】 直角三角形斜边上的中线等于斜边的一半
\triangle BEF \sim \triangle ABD- 欲证明
EG=GC,而GC=NG,根据直角三角形的中线定理可知,如果我们能证明\triangle NEC为直角三角形即可。
Q:如何证明一个三角形是直角三角形呢?
A:通过勾股定理肯定可以,这里用不上,只能从角度方向去思考:
通过瞪眼大法得知:
如果真有这个\triangle NEC=90^\circ,那么\angle NEF=\angle BEC(两个直角+一个共用的角)
我们现在知道:EF:EB=1:2,DC=NF:BC=1:2
\therefore EF:EB=NF:BC
因为\tan \alpha=1/2
90^{\circ}-\angle 1+\angle 2 +(90^{\circ}-\angle 1)=180^{\circ}
\therefore \angle 2=2 \times \angle 1
即两个成比例边的夹角:\angle EBC=\angle EFN
\therefore \triangle BEC \sim \triangle FEN,都扣去\angle FEC,则证明了\angle CEN=90^ \circ
证毕。
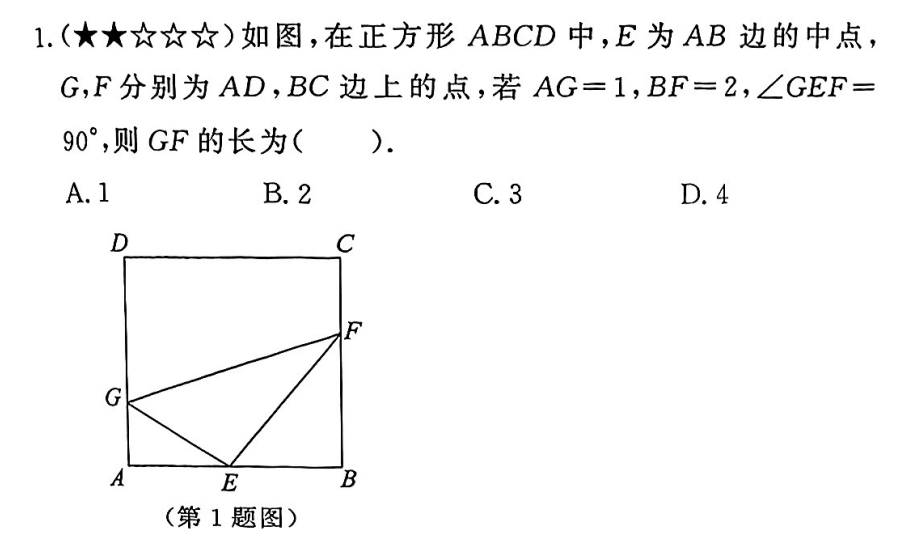
【前导知识】
\triangle AEG \sim \triangle BFE
比例:
\frac{AE}{BF}=\frac{AG}{BE}
同时:
AE=BE
\therefore AE^2=AG . BF=2
\therefore AE=\sqrt{2}
\therefore GF^2=CE^2+EF^2=AG^2+AE^2+BE^2+BF^2=1+2+2+4=9
\therefore GF=3
\triangle EFC \cong \triangle DAE
EF=AE
BF=BC-FC=BC-AD=5
AF=\sqrt{AB^2+5^2}=\sqrt{144+25}=13
\therefore \large AE=\frac{13}{2}
\triangle ODE \cong \triangle AOB
CO是垂直平分线,证毕
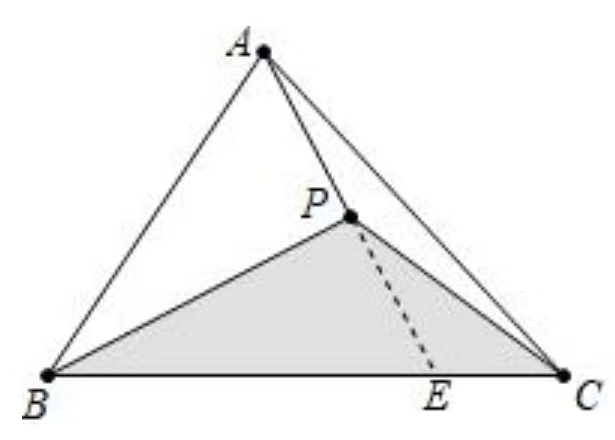
\triangle APB \cong \triangle BPE
S_{\triangle PEC}=S_{\triangle APC} 底边长度一样,高相同。
所以阴影面积是一半的面积。
CD平分\angle ACB, BD \perp CD
\triangle EBC是等腰直角三角形
AE=BE=BD+D1+1=2
选A
\triangle AEG \cong \triangle AEC
ED为\triangle GCB中位线 BF=(AB-AC)/2
答:是1/2的概率
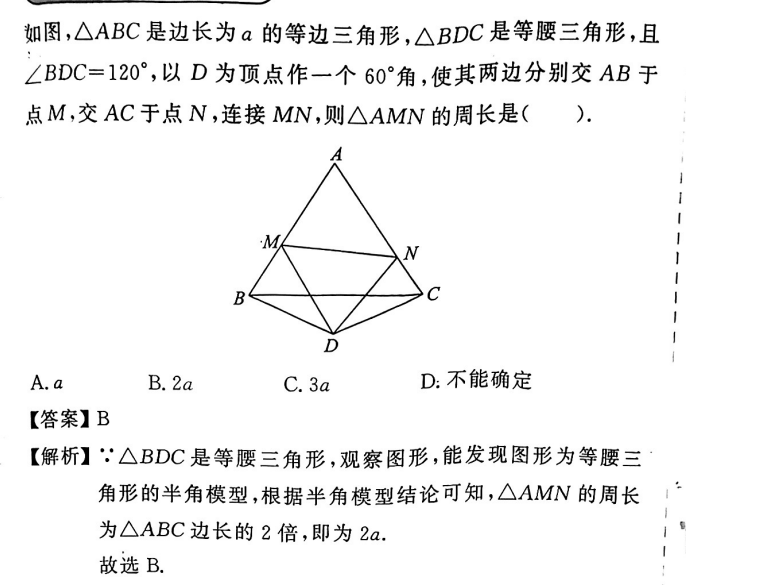
前导知识
【中考热点】基本模型——半角模型 视频
画图解析:
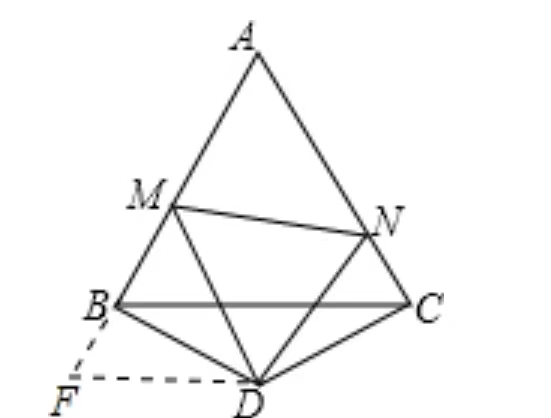
题解
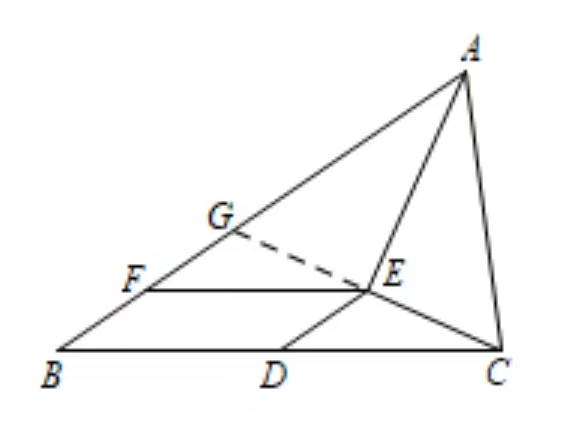
因为\triangle AMN的周长需要三长边AM,MN,AN,而分别计算出来并加在一起从题目中给出的条件看来并不现实,所以需要将一条边转化到另一条边上去,这样就可以拿到两条直边,看看能不能和题目给出的AB、AC建立起关系。
通过瞪眼大法得知,AN=AC-CN,所以,尝试将CN移动到AB上去,一旦成功转化,就好办了。
引辅助线:在AB延长线上截取BF=NC,试图证明\triangle BDF \cong \triangle DNC,很显然,通过ASA(BD=DC,NC=BF,\angle FBD= \angle DCN),全等三角形得证。有条件 DF=DN 成立。
现在还拿不到结论,还需要继续瞪眼大法:
\angle BDM+\angle MDN + \angle NDC= 120^ \circ
而其中\angle MDN=60 ^ \circ
\therefore \angle BDM+\angle NDC=60 ^ \circ
而\angle NDC=\angle BDF,所以\angle MDF=60^\circ ①
MD是公共边 ②
DF=DN ③
\therefore \triangle MDF \cong \triangle MDN (SAS)
\therefore MN=MB+BF
C_{\triangle AMN}=AM+MN+AN=AM+MB+BF+AN=AB+BF+AN=AB+AN+NC=AB+AC=2a
第二问也是成立的,因为两角相加等于180,也就是互补,一样可以证明两个三角形全等。
下面解决第三问:

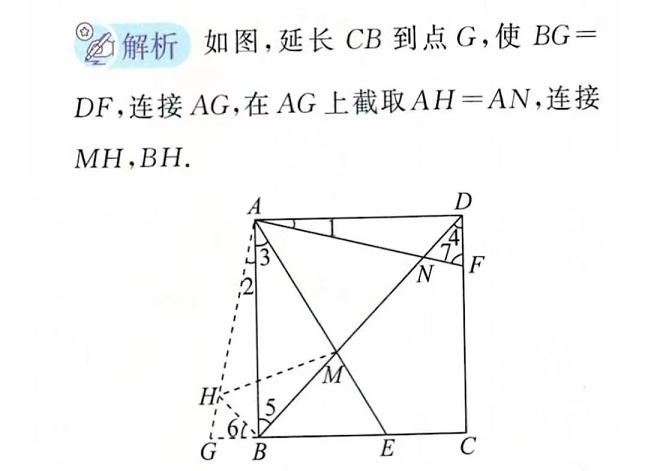
\triangle BAG \cong \triangle DAF \Rightarrow \angle BAG=\angle DAF,AG=AF
\angle BAG + \angle EAD= \angle DAF + \angle EAD=\angle EAF = \frac{1}{2} \angle BAD
将\angle DAF移动到\angle BAG后,这块多出来的小角就存在于原始角\angle BAD中了,扣除它后,再扣除\angle EAD,则剩下的\angle GAE就是\frac{1}{2}\angle BAD=\angle EAF
\therefore \triangle AGE \cong \triangle EAF
\therefore EG=EF
\because EG=BE-BG
\therefore EF=BE-FD 所以,题目中说到的结论是错误的。
本题是例题,不再讲解
通过两次三角形全等,可知\angle GAE=\angle EAF,FN=GH \Rightarrow \triangle DFN \cong \triangle BGH
BM^2+DN^2=BM^2+BH^2=MH^2=MN^2
\because DN=1,BM=2
\therefore 2^2+1^2=MN^2
\therefore MN=\sqrt{5}
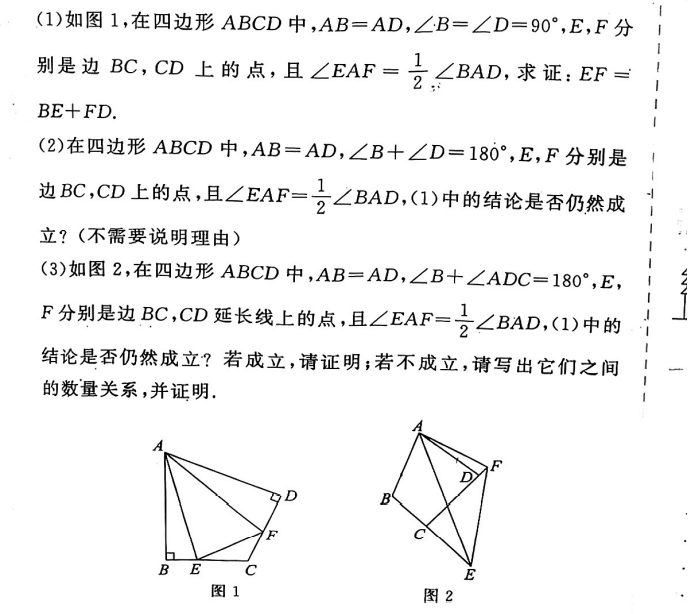
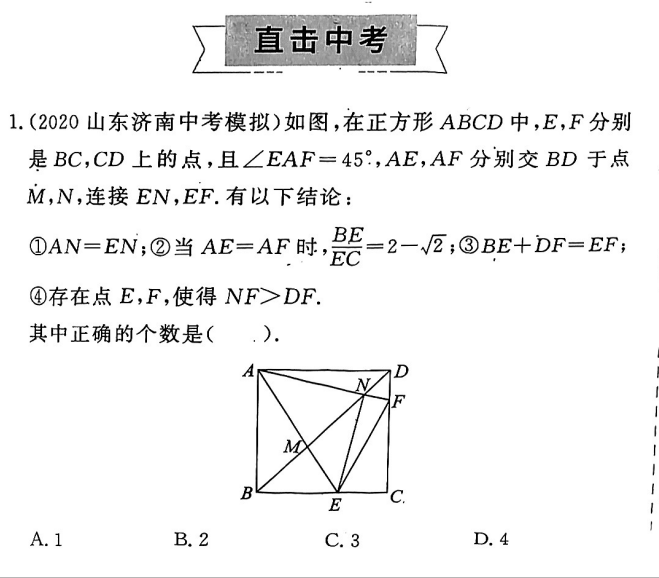
1、证明 AN=EN
\because \angle AMN=\angle BME,\angle EAN=45^ \circ =\angle ABM
\therefore \triangle AMN \sim \triangle BME
\large \therefore \frac{AM}{BM}=\frac{MN}{ME}
同时,\angle AMB=\angle BMN
\therefore \triangle AMB \sim \triangle NME
\therefore \angle AEN=\angle BAE=45 ^ \circ
同时因为\angle EAN=45 ^ \circ
\therefore \angle ENA=90^\circ
也就是\triangle ANE为等腰直角三角形 ,所以 AN=NE, ① ✔
2、证明 当AE=AF时,\frac{BE}{EC}=2-\sqrt{2}
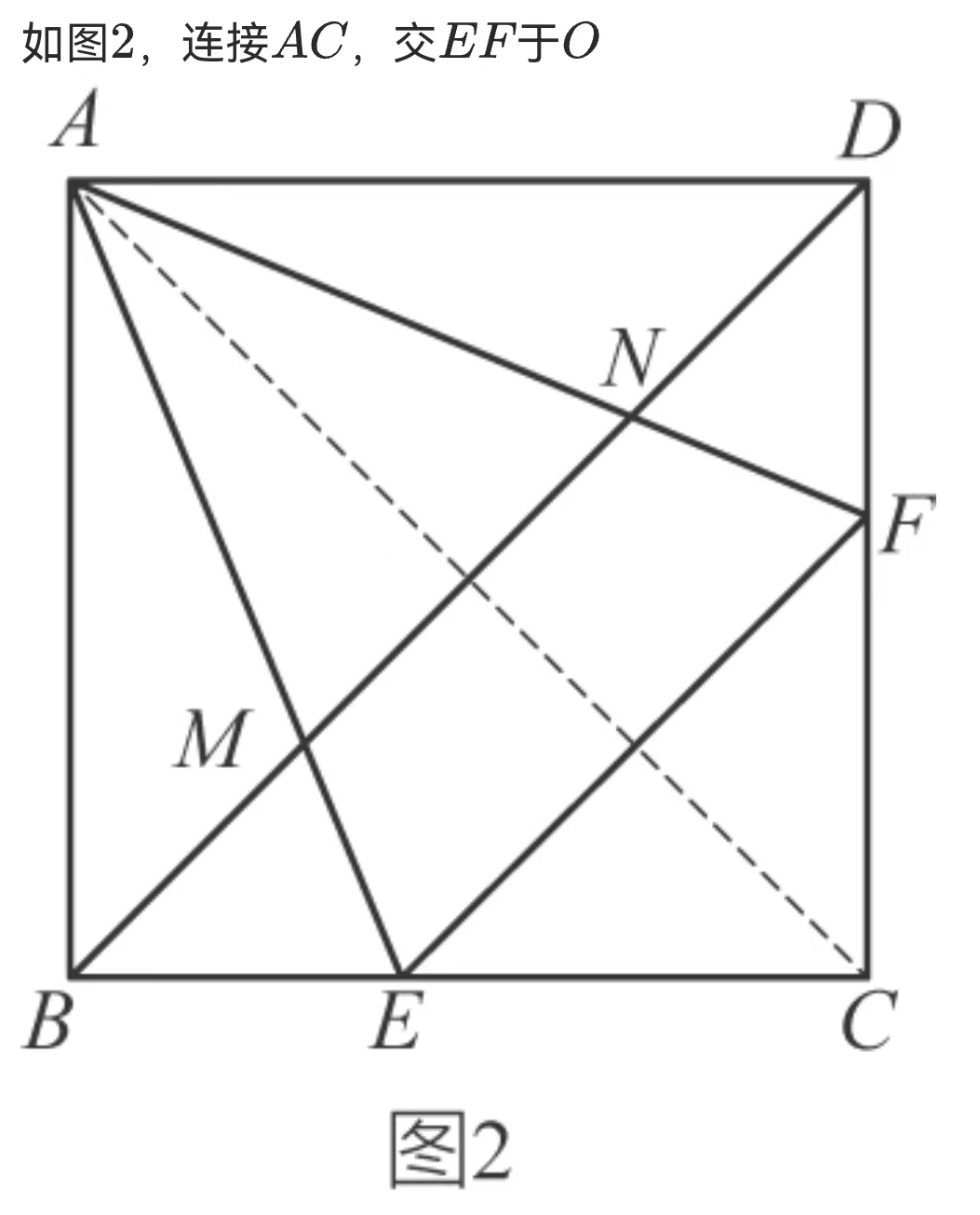
设正方形边长为1,设CE=x,\Rightarrow OC=\frac{\sqrt{2}}{2}x
\triangle AOE \cong \triangle ABE \Rightarrow AO=AB=1 \Rightarrow CO=\sqrt{2}-1
\therefore 1+ \frac{\sqrt{2}}{2}x=\sqrt{2} \Rightarrow x= 2- \sqrt{2}
\large \frac{BE}{EC}=\frac{1-(2-\sqrt{2})}{2-\sqrt{2}}=\frac{\sqrt{2}}{2}
故 ② ✘
3、证明BE+DF=EF
半角模型常见办法,就不再赘述了。 ③ ✔
4、证明 存在点E,F,使得NF>DF
这是一个大边对大角,小边对小角的知识点考查,\angle NDF=45 ^ \circ,\angle FND=\angle NDA + \angle NAD=45^ \circ+\angle NAD
\therefore \angle DNF> \angle NDF,\Rightarrow DF>NF ④ ✘
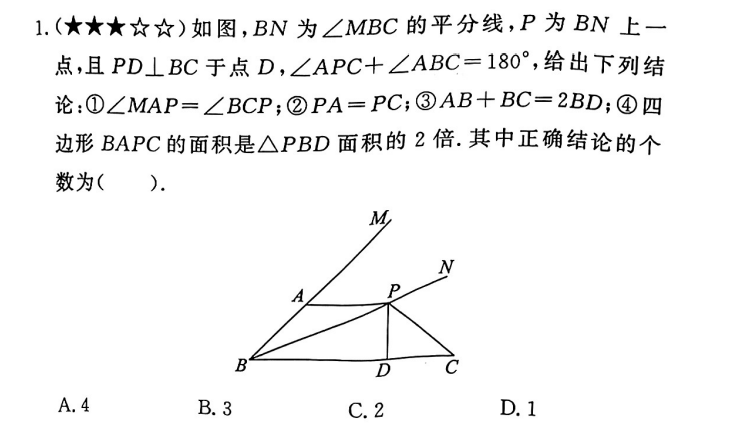
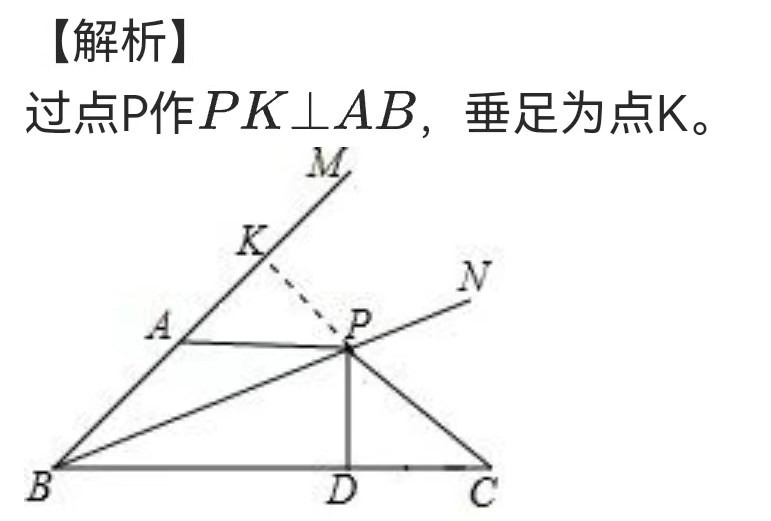 证明
证明\triangle BPK \cong \triangle BPD ①
\angle PKA=\angle PDC =90 ^ \circ ②
KP=PD ③
\therefore \triangle APK \cong \triangle PDC
所以第一问、第二问、第三问(稍一修改即可)都正确。
第四问:将\triangle PDC 旋转到\triangle PKA,S_{PCBA}=S_{\triangle BKP}+S_ { \triangle BPD} ,所以也正确。