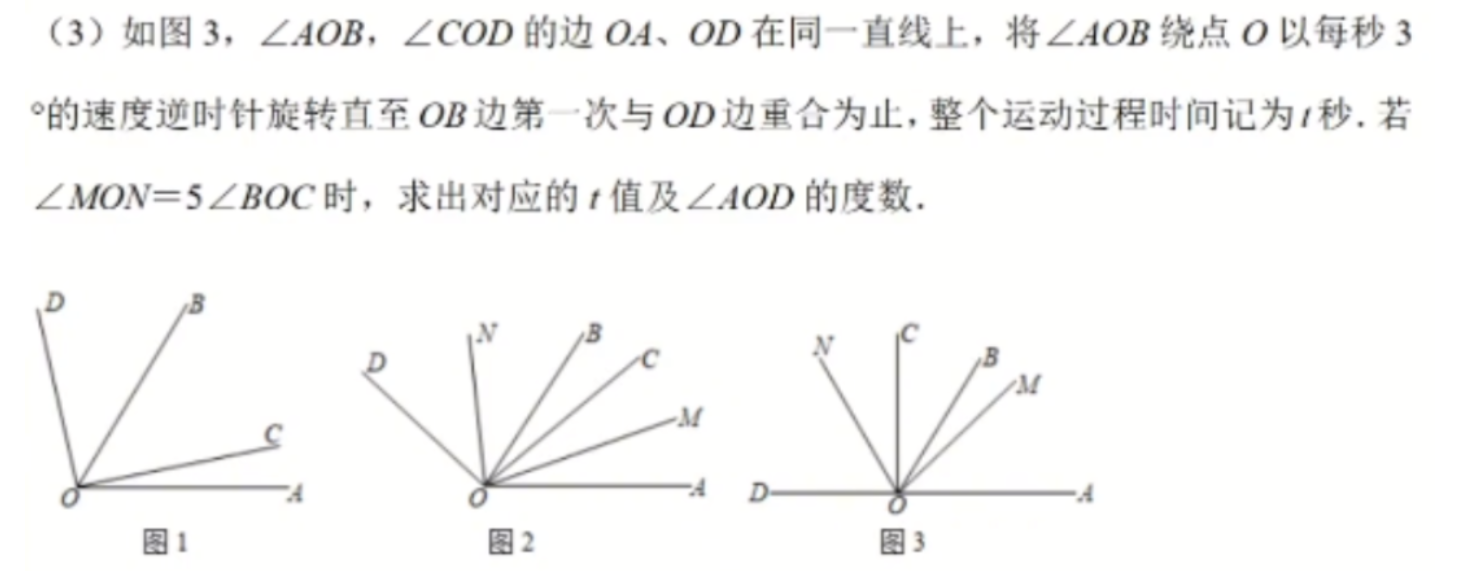
2.7 KiB
(1) 用已知换未知就是办法
\angle AOD = \angle AOB+\angle BOD
=60^{\circ}+\angle BOD
\angle BOC=\angle COD-\angle BOD
=90^{\circ}-\angle BOD
\angle AOD+ \angle BOC=60^{\circ}+90^{\circ}+\angle BOD-\angle BOD=150^{\circ}
\angle BOD-\angle AOC=\angle COD-\angle BOC-(\angle AOB- \angle BOC)=90^{\circ}-60^{\circ}=30^{\circ}
(2)
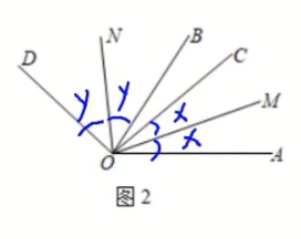
\angle MON=x+y+\angle BOC=\frac{1}{2}(\angle AOC+\angle BOD)+\angle BOC
=\frac{1}{2}(\angle AOB -\angle BOC+\angle COD-\angle BOC)+\angle BOC
=\frac{1}{2}(90^{\circ}+60^{\circ})=75^{\circ}
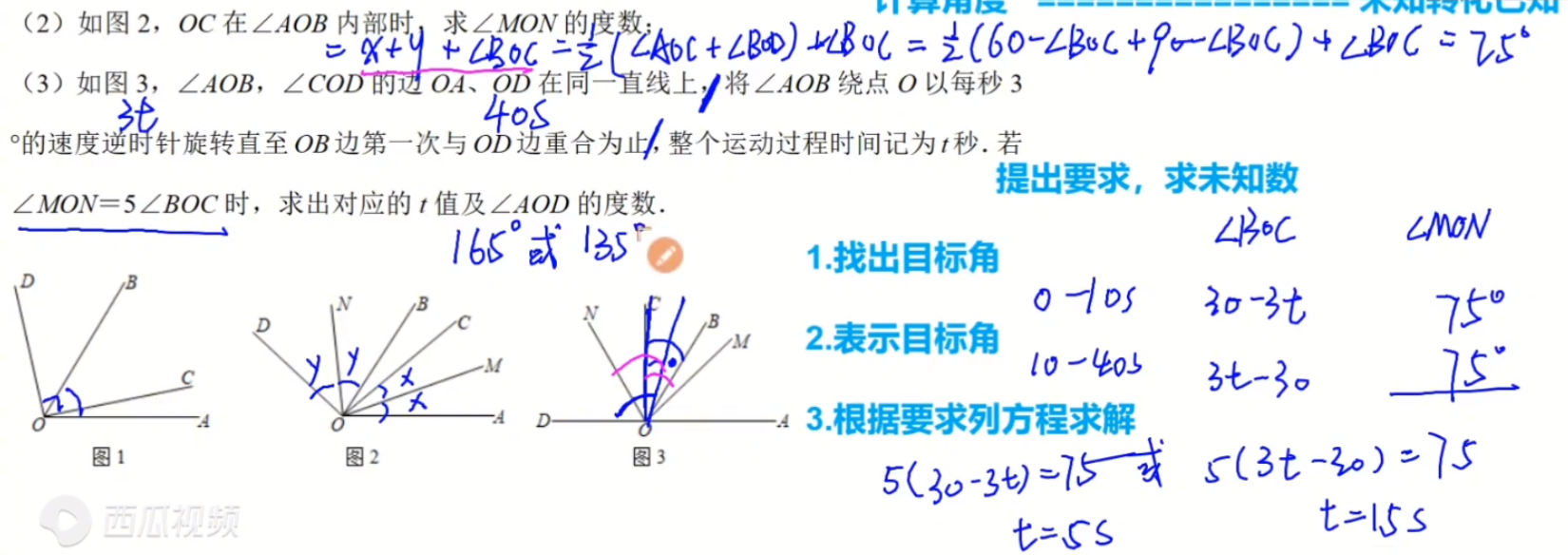
(3)常见的第二种问题,一般会有一个未知数
解决方法:
- 找出目标角
- 表示目标角
- 根据要求列方程求解
- 任意时刻旋转的角度都是
3t \angle AOB=60^{\circ},到OD止,OB共需走的角度是120^{\circ},也就是,当t=40时,走完全程。- 重点是表示
\angle BOC和\angle MON,这是 重难点
\because \angle AOB=60^{\circ},\angle AOC=90^{\circ}
\therefore \angle BOC=90^{\circ}-60^{\circ}=30^{\circ}
当OB开始旋转时,分两种情况:
OB'在OC右侧,此时\angle B'OC=30^{\circ}-3tOB'在OC左侧,此时\angle B'OC=3t-30^{\circ}
-
算一下临界值:
30^{\circ}-3t=0^{\circ}此时t=10,表示10秒之内,在右侧,等于10秒时,与OC重合 -
第二种情况是在
10\sim 40秒之间,此时 完全符合第二问的答案,即OC在\angle AOB内部!此时,\angle MON=75^{\circ}
情况1中\angle MON是多大呢?借鉴第二问的思路:
\angle MON=x+y-\angle BOC=\frac{1}{2}(\angle AOC+\angle BOD)-\angle BOC
=\frac{1}{2}(\angle AOB +\angle BOC+\angle COD+\angle BOC)-\angle BOC
=\frac{1}{2}(90^{\circ}+60^{\circ})=75^{\circ}
即:两种情况下,都是\angle MON=75^{\circ}
5(30-3t)=75^{\circ}
或
5(3t-30)=75^{\circ}
解得t=5或t=15
依题意,\angle AOB在一同旋转,OB走多少度,OA就走多少度,而OD是不动的,所以180^{\circ}减去走的角度即可:
\angle AOD=180^{\circ}-3*5=165^{\circ}
或
\angle AOD=180^{\circ}-3*15=135^{\circ}