You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
1.0 KiB
1.0 KiB
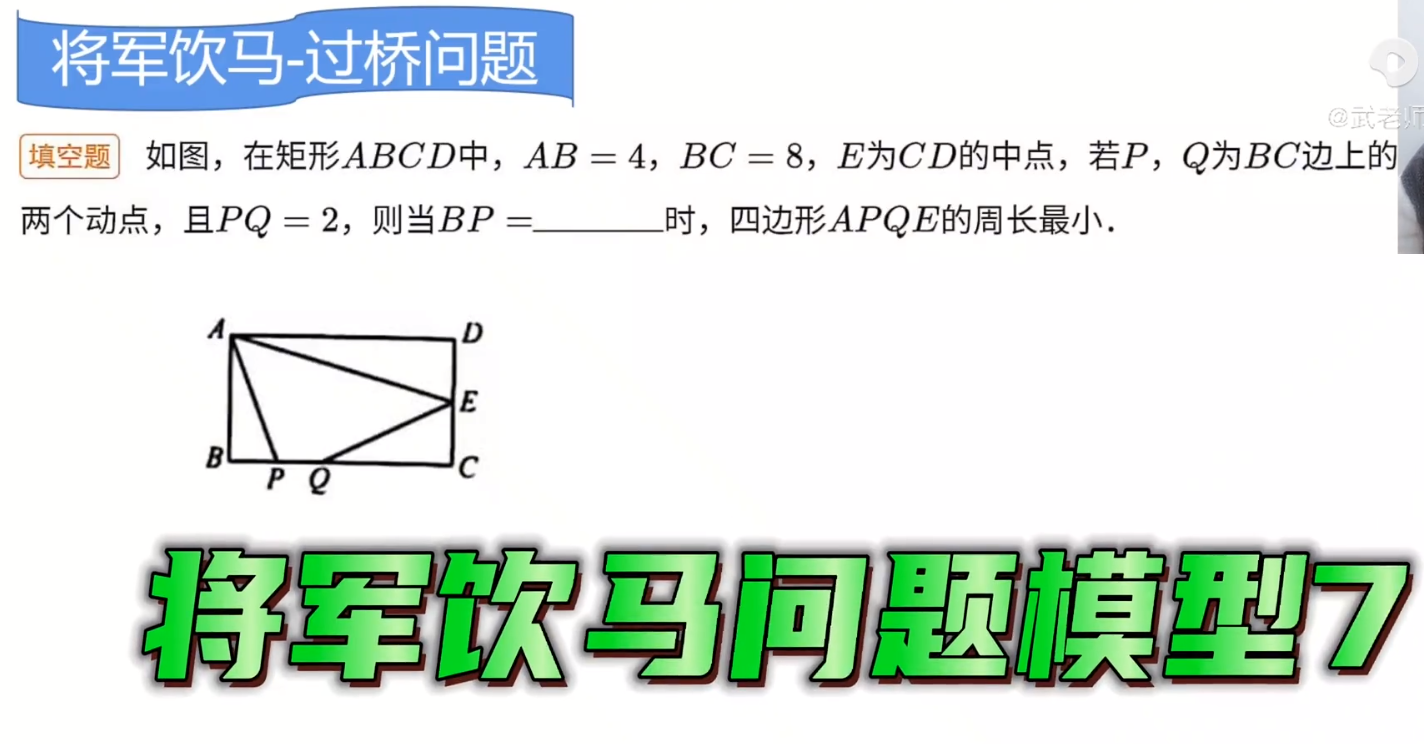
思路:
C_{APEQ}=AP+PQ+QE+AE
此时我们发现AE的长度是固定的,PQ也是固定的长度=2,所以,就是求AP+QE的最小值。
两个线段和的最小值,有点像将军饮马,但这两个线段没有公共端点,所以不能用以前的结论。
考虑到PQ的长度是固定的,可以从P向AD引出一条AP的平行线,交AD于A'点。
然后将E做一个BC的对称点E',这样,A'E'就是两点间线段最短,就是最小值。
但本题没有问题最小值是什么,而是说BP等于什么的时候能取得最小值。我们只要能计算出Q'的位置,再减2就是BP的位置了。
\because EC=CE'=2
\therefore \angle DE'A'=45^{\circ}
\therefore Q'C=CE'=2
\therefore BQ'=8-2=6
\therefore BP=6-4=2