python/数学课程/将军饮马问题/模型6.md

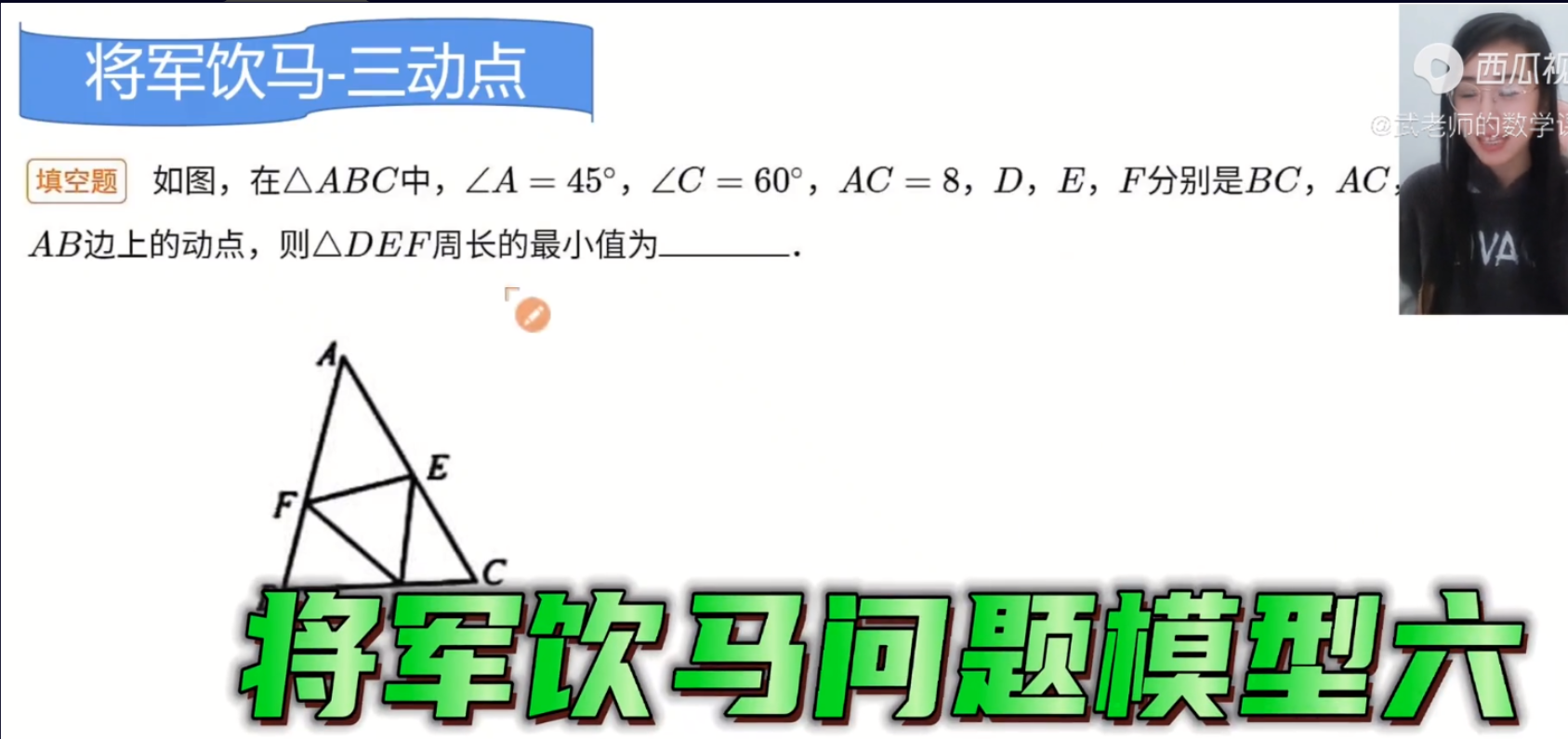
三个点都是动点，不太好整，我们可以先视其中一个点为定点，然后再想办法继续求解，现在视D为定点，从D引关于AB,AC对称的对称点D_2,D_1 ,则D_1D_2应该就是最小值，其中D_1D_2与AB,AC的交点就是F,E点。

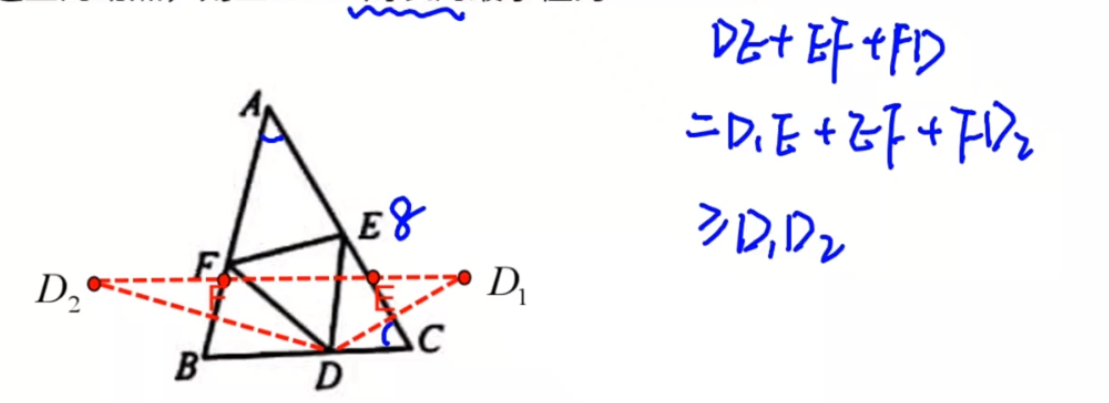
现在的问题转化为D_1D_2就是最短的，但问题是D_1D_2不是唯一的，也没有求解出来答案啊！

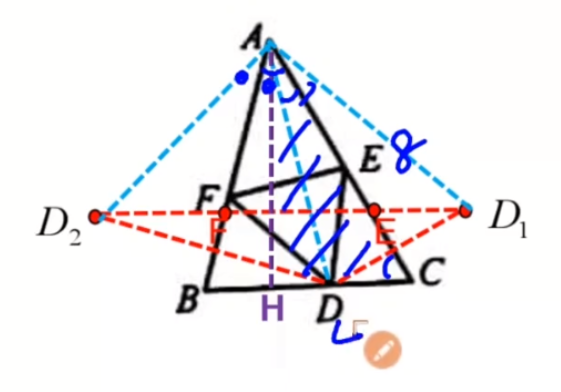
我们继续思考,由于AB是DD_2的垂直平分线，AC是DD_1的垂直平分线，所有有\angle D_2AB=\angle BAD,\angle DAC=\angle CAD_1 而 \angle BAC=45^{\circ},所以\angle D_2AD_1就是我们梦寐以求的直角三角形！！ D_2D_1就是斜边！！

AD_2=AD=AD_1,所以\triangle AD_2D_1是直角等腰三角形。

现在如果我们能求解出AD_2,那么\sqrt{2}AD_2就是答案。 AD_2什么时候最短呢？也就是AD什么时候最短呢？很显然，就是从A做一条BC的垂线时最短！引辅助线AH \perp BC,\sqrt{2}AH就是答案！

而\angle ACD=60^{\circ},所以CH=1/2AC=4 \therefore AH=\sqrt{8^2-4^2}=4\sqrt{3}

所以答案：4\sqrt{3} \times \sqrt{2}=4\sqrt{6}