python/数学课程/将军饮马问题/模型4.md

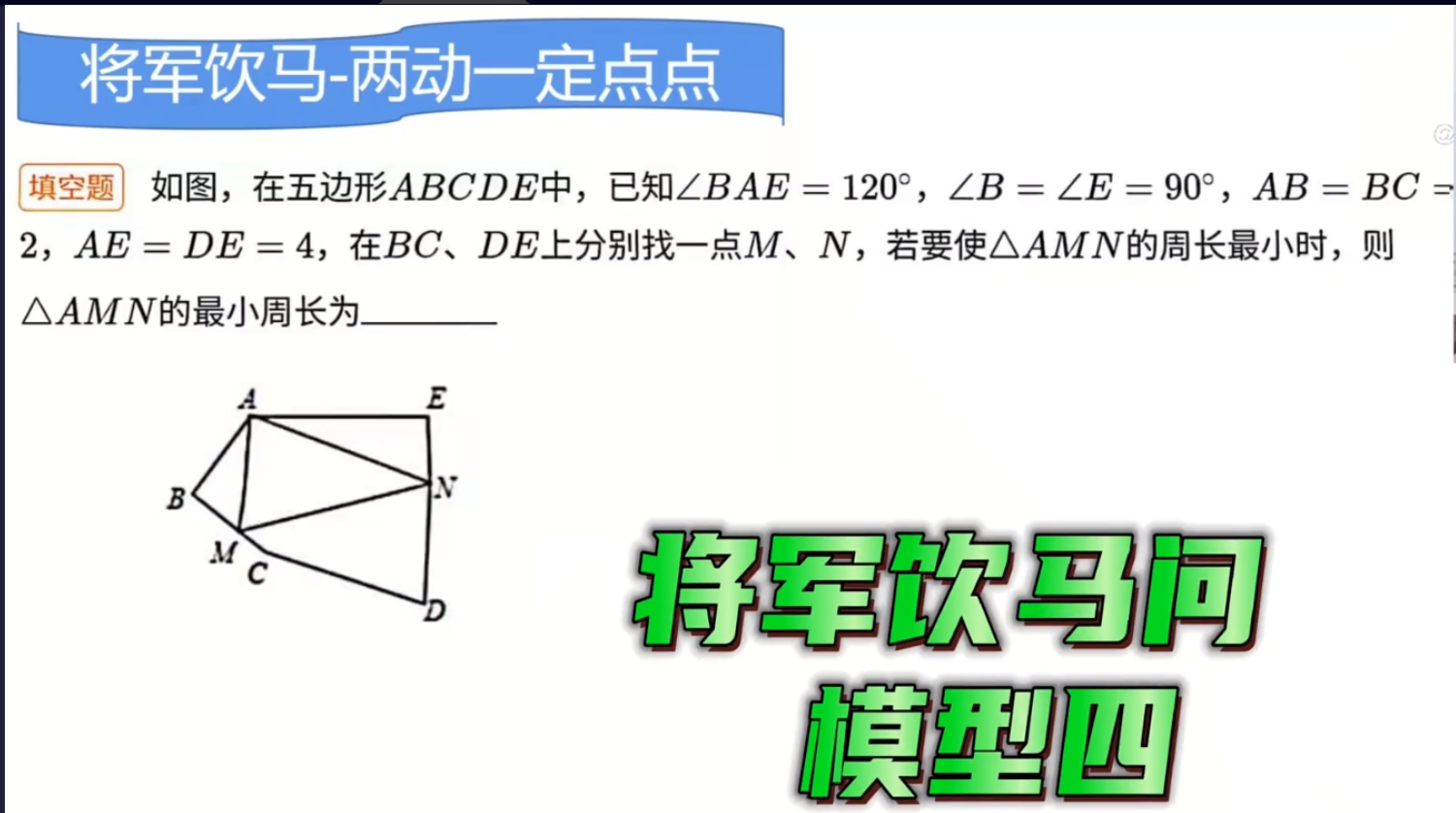
• A是定点，而M,N是动点，一个定点两个动点。
• 原来的模型1，2，3都是求的两个线段的线段和最小值，现在是求三条线段的线段和最小值。

辅助线

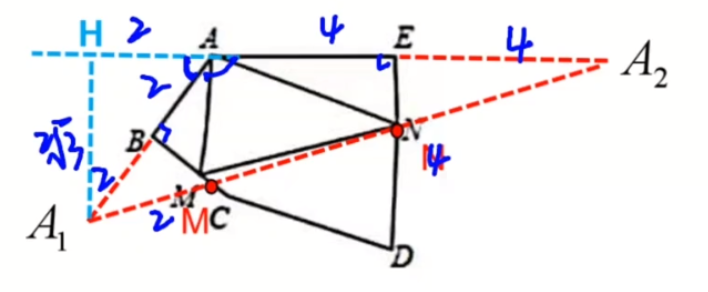
• 找到A关于BC的对称点A_1,因为\angle ABC=90^{\circ},所以A,B,A_1三点共线,同理，作出,A关于EN的对称点A_2,则A,E,A_2三点共线。

经过上面的引入辅助线，AM+MN+AN就转化为A_1M+MN+NA_2,我们可以很容易得到结论：当A_1,A_2,M,N在一条直线上时，AM+MN+AN最短。

那么A_1A_2的长度是多少呢？它不在任何一个直角三角形中，不好求。只好构建一个直角三角形，由A_1向AE引一条垂线AH，因为\angle A_1AA_2=120^{\circ},所以\angle A_1AH=60^{\circ},因为\angle A_1H=90^{\angle},所以\angle AA_1H=30^{\circ}

AB=A_1B=2,所以 A_1A=4 \Rightarrow AH=2 \therefore A_1H=\sqrt{4^2-2^2}=2\sqrt{3} A_1A_2=\sqrt{10^2+12}=4\sqrt{7}

思考题：似乎题目中给出的AB=BC,AE=ED并没有使用得上。从上面的解题过程来看，似乎C,D也是可以向上移动的，并不影响最终的四点共线，也就是说:这两个条件真的没用。

总结

• 求三角形的周长最小值，需要转化为求两点之间线段最短，是哪两个点呢？可以考虑使用两次将军饮马，作两个对称的点。
• 计算长度，一般只能是给出特殊角度，特殊角度也只能是在直角三角形中求解才行。引导我们想办法构建一个直角三角形解决问题。