You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
1.2 KiB
1.2 KiB
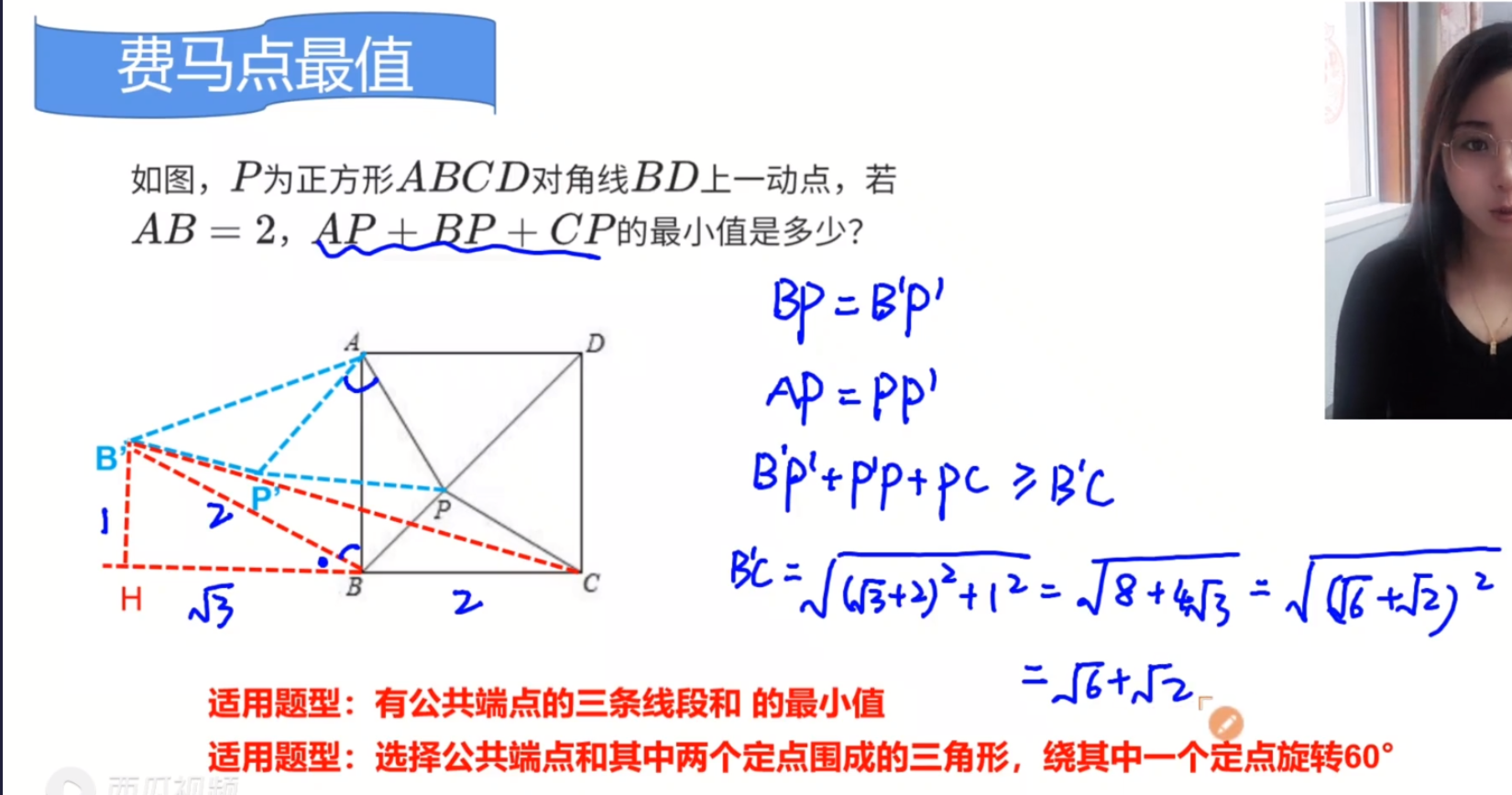
有公共端点的三条线段,方法就是找出两条线段所在三角形做60^{\circ}旋转。
如下图:
\because \triangle AB'P' \cong \triangle ABP
\therefore \angle PAP'=60 ^{\circ},AP=AP'
\therefore \triangle AP'P是等边三角形
\therefore AP=PP'
问题中要求解的AP+BP+PC也就成功转化为
PP'+B'P'+PC通过图形可知,图中B'C就是三点共线时的最小值!
下面开始求解B'C长度。
求边形一般用勾股定理,构造直角三角形:从B'向BC边引垂线,交BC延长线于H。
\because \triangle AB'B是等边三角形
AB=B'B=2 可以理解为旋转了60^{\circ}
\because \angle ABB'=60 ^{\circ}
\therefore \angle B'BH=30^{\circ}
\therefore B'H=1,BH=\sqrt{3}
\therefore B'C=\sqrt{(\sqrt{3}+2)^2+1^2}=\sqrt{8+4\sqrt{3}}
复合二次根式 需要用配方法化简:
=\sqrt{8+2\sqrt{12}}=\sqrt{\sqrt{6}^2+2\sqrt{12}+\sqrt{2}^2}=\sqrt{(\sqrt{6}+\sqrt{2})^2}=\sqrt{6}+\sqrt{2}