You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
1.6 KiB
1.6 KiB
### 将军饮马问题
唐朝诗人李颀的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河． ”
诗中隐含着一个有趣的数学问题．
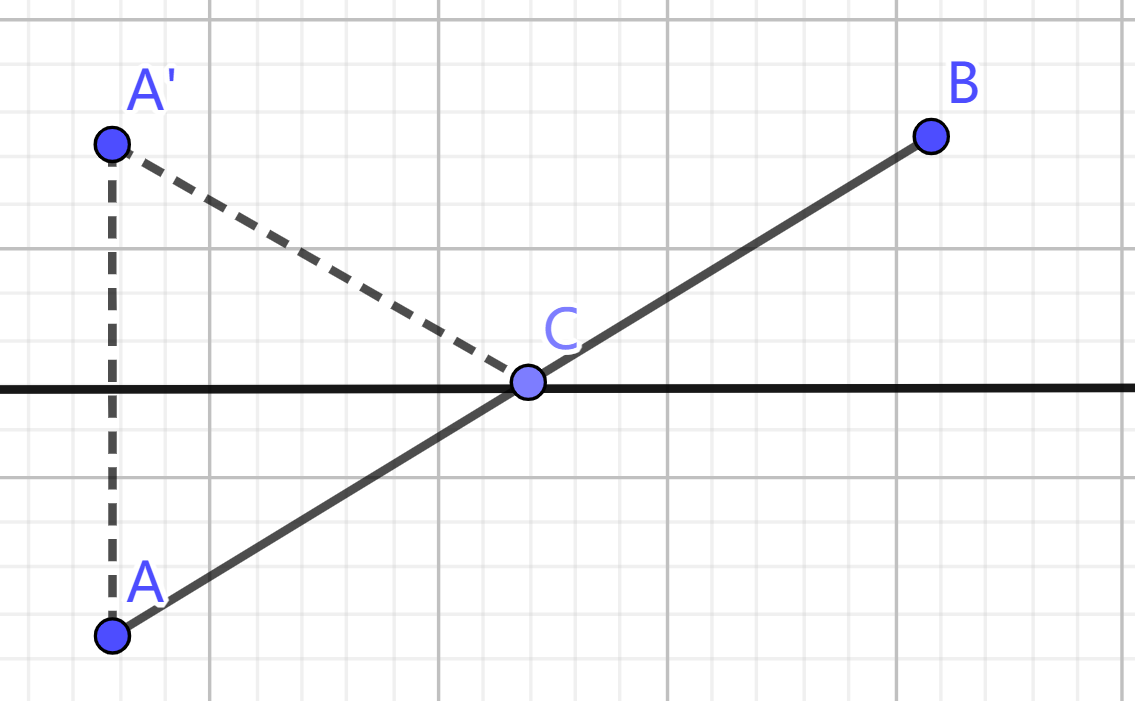
如图所示，诗中将军在观望烽火之后从山脚下的A'点出发，走到河边饮马后再到B点宿营．求怎样走才能使总的路程最短。
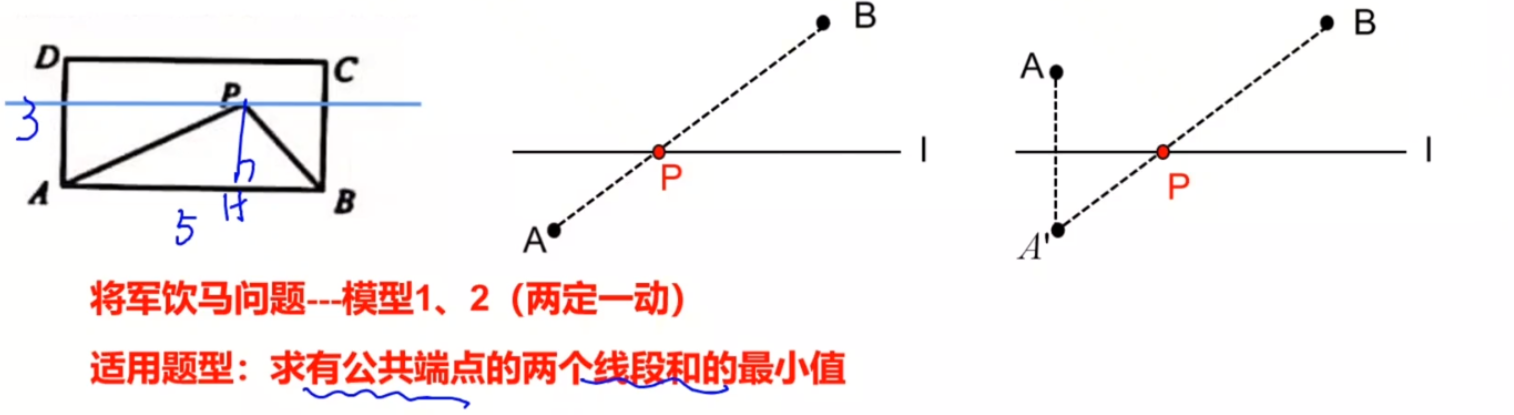
模型1
就是两点之间直线最短，A,B在岸的两边，所以从A向B连一条线段，就是最短长度。
模型2
A,B在岸的同一边，此时，将A关于河（直线）做对称，找到A'点，其中AC=A'C,所以动点C必然在对称点与B的连接线与河的交点上。
例题：
解题思路：
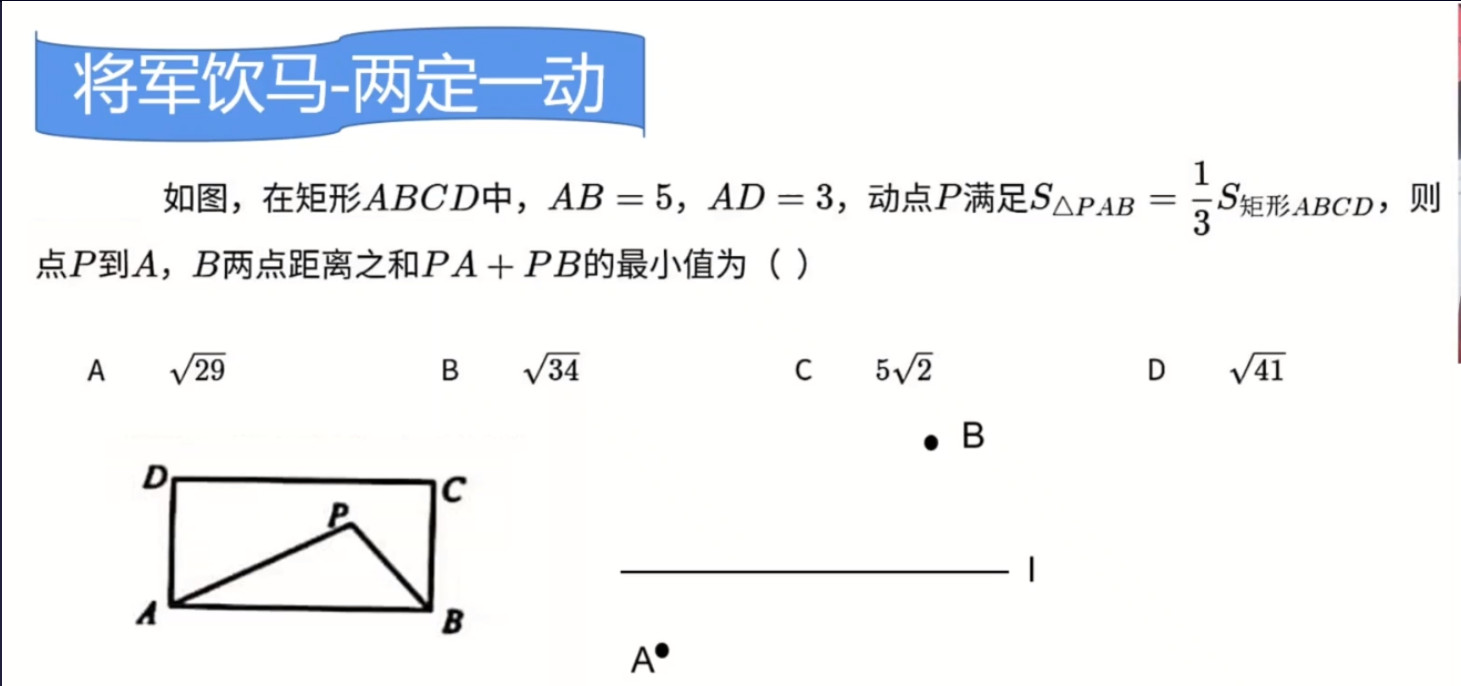
P到A,B两点的距离和，很自然想到了将军饮马。
一个三角形面积的关系式，让我们很迷惑，把它翻译一下：
S_{\triangle PAB}=\frac{1}{3}S_{矩形ABCD}
由P向AB引一条垂线，计为PH,
则有：
1/2 \times AB \times PH = 1/3 \times AB \times AD
\therefore PH=2
所以，将A关于PH=2这条直线做对称，找到A'
AA'=4,而AB=5,所以A到B最短距离就可以通过勾股定理计算斜边得到\sqrt{4*4+5*5}=\sqrt{41}
答案：D