2.0 KiB
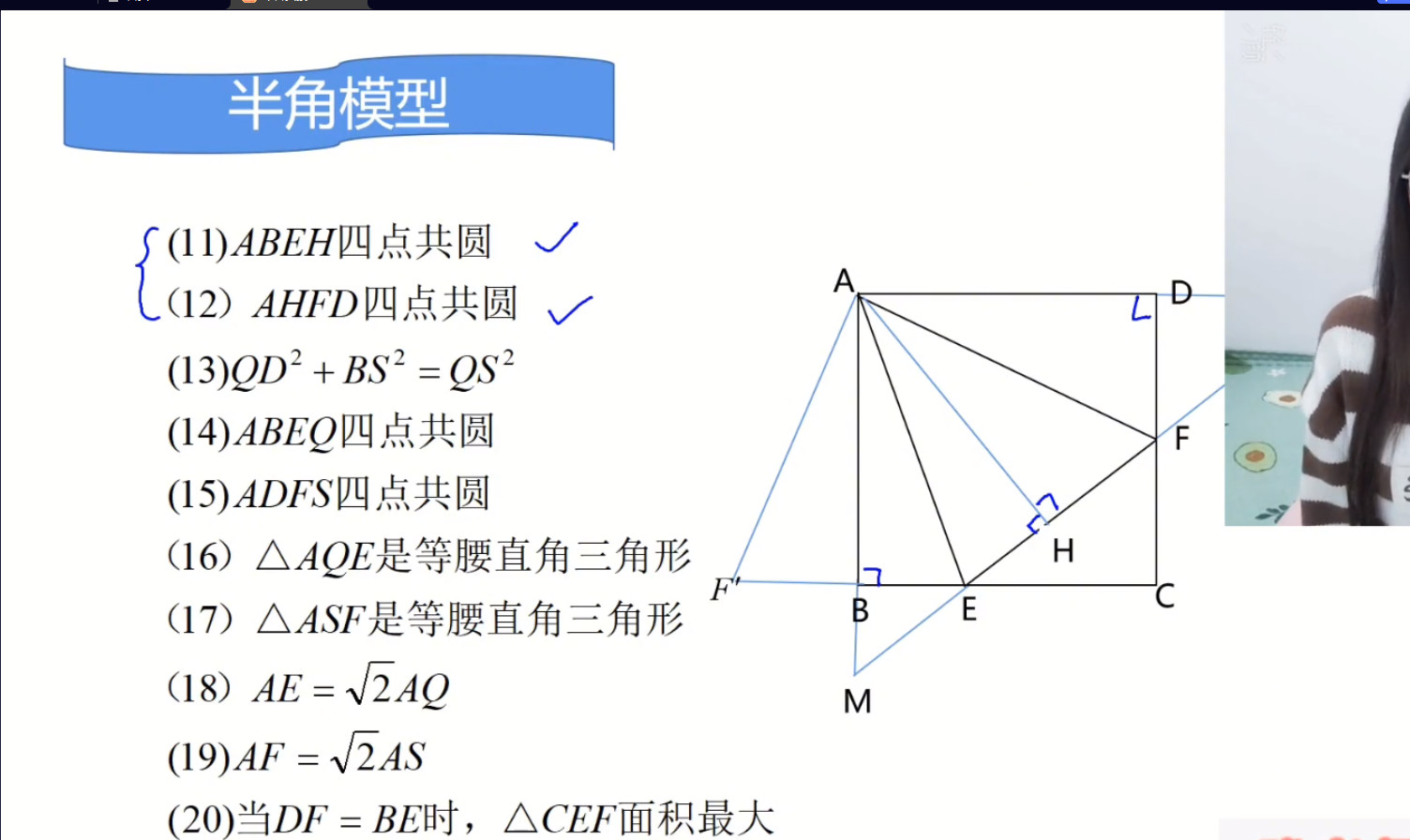
(11) 四点共圆的条件是:圆内接四边形的对角互补
\because \angle ABE=\angle AHE=90^{\circ}
\therefore ABEH四点共圆
 (
(12) 同理:\because \angle AHF= \angle ADF=90^{\circ}
\therefore AHFD四点共圆
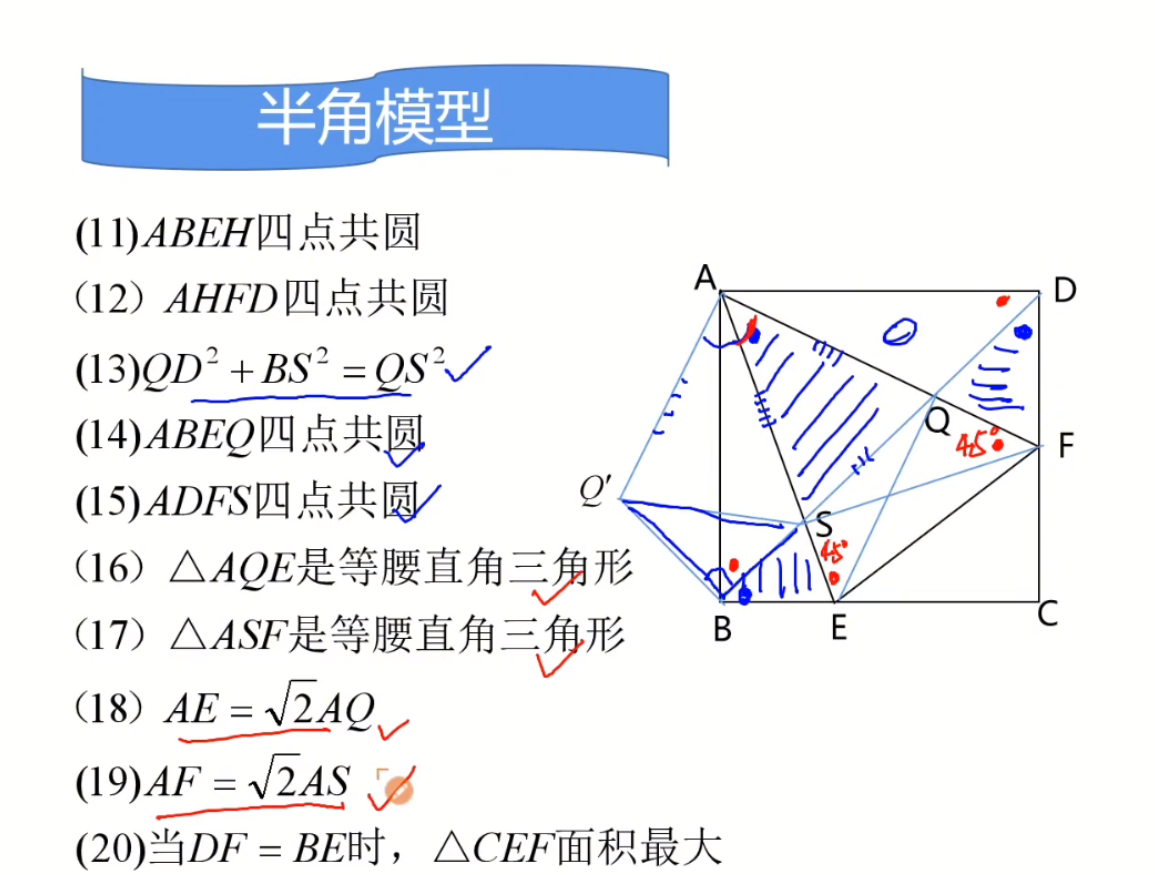 (
(13) 很明显QD与BS不在同一个三角形中,不太好直接证明两者间的关系,我们采用的办法是旋转法,将\triangle AQD旋转到AQ'B的形式上。
因为是旋转,所以BQ'=QD,问题得到转化。
下面来研究一下Q'B^2+BS^2=QS^2吗?
根据以前的证明经验,我们知道\triangle Q'SA \cong \triangle ASQ (SAS)
\therefore Q'S=QS
问题也就转化为让我们证明\angle Q'BS=90^{\circ}
\angle Q'BS=\angle ABQ'+\angle ABS=\angle ADQ+\angle ABS=45^{\circ}+45^{\circ}=90^{\circ}
证毕
(14)性质:共圆的四个点所连成同侧共底的两个三角形的顶角相等
\angle DBC=\angle EAF=45^{\circ}
所以EBAQ四点共圆,证毕
(15) 同14,有\angle EAF=\angle BDC=45^{\circ}
所以ADFS四点共圆
(16) 利用上面ABEQ四点共圆的结论,所以弧AQ的两个对应角\angle ABD=\angle AEQ=45^{\circ}
而且已知\angle EAF=45^{\circ}
\therefore \angle AQE=90^{\circ}
\therefore \triangle AEQ是等腰直角三角形
证毕
(17) 根据上面的结论ASFD四点共圆,弧AS对的两个角\angle ADS=\angle AFS=45^{\circ}
\therefore \triangle ASF是等腰直角三角形
证毕
(18,19)因为有上面16,17的结论,所以\sqrt{2}倍的结论也是正确的
(20)
视频证明
今日头条:武老师课堂