|
|
|
|
|
|
|
|
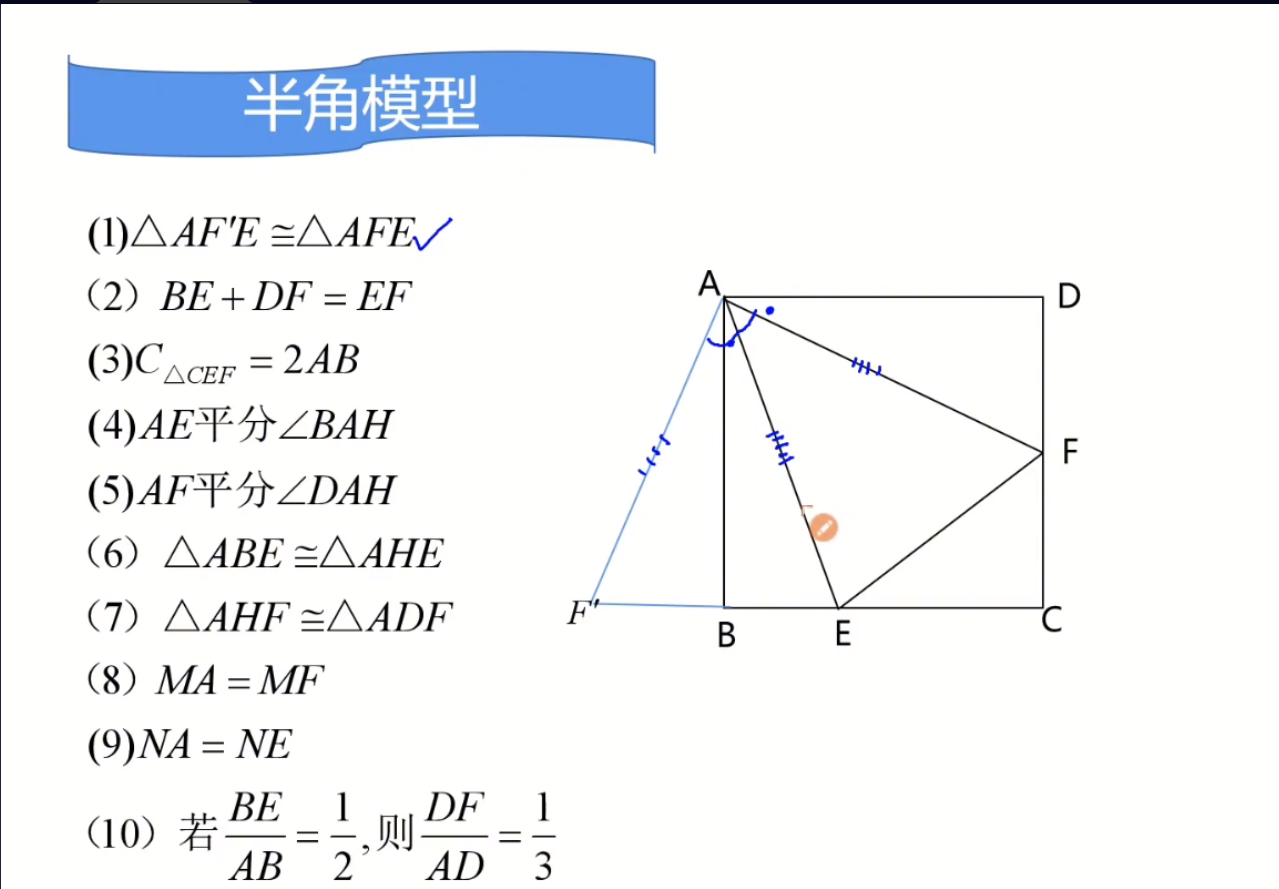
将$\triangle AFD$ 旋转到$ABF'$,因为$\angle D=90^{\circ}$,所以$F',B,E,C$共线。
|
|
|
|
|
|
因为是旋转得到$\triangle AF'B$,所以$\triangle AF'B \cong ADF$
|
|
|
|
|
|
所以$DF=BF',\angle DAF=\angle BAF'$
|
|
|
双因为$\angle BAE +\angle FAD=45^{\circ}$
|
|
|
所以$\angle F'AB+\angle BAE=\angle F'AE=45^{\circ}$
|
|
|
|
|
|
$AF'=AF,\angle F'AE=\angle EAF,AE=AE$ 根据$ASA$,所以$\triangle F'AE \cong \triangle EAF$ ①**证毕**
|
|
|
|
|
|
$BE+DF=BE+BF'$ 旋转得到
|
|
|
$BE+BF'=EF$ ②**证毕**
|
|
|
|
|
|
$EF=EF'=BE+BF'=BE+FD$
|
|
|
$\therefore C_{\triangle CEF}=CE+CF+EF=CE+CF+BE+FD=BC+CD=2AB$ ③**证毕**
|
|
|
|
|
|
----
|
|
|
|
|
|
|
|
|
|
|
|
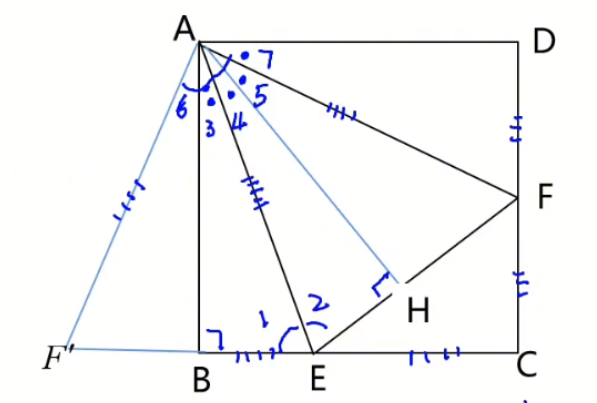
因为$\triangle AF'E \cong \triangle AEF$
|
|
|
$\therefore \angle 1=\angle 2$
|
|
|
$\therefore \triangle BAE \cong EAH$ ⑥**证毕**
|
|
|
|
|
|
$\therefore \angle 3=\angle 4$
|
|
|
因此$AE$是$\angle BAH$平分线,④**证毕**
|
|
|
|
|
|
|
|
|
**求证**:$\angle 5=\angle 7$
|
|
|
$\because \angle 4+\angle 5=45^{\circ}$
|
|
|
$\because \angle 3=\angle 4$
|
|
|
$\therefore \angle 3+ \angle 5=45^{\circ}$
|
|
|
|
|
|
$\because \angle 7 + \angle 3=90^{\circ}-\angle EAF=90^{\circ}-45^{\circ}=45^{\circ}$
|
|
|
|
|
|
$\therefore \angle 5=\angle 7$
|
|
|
|
|
|
所以,$AF$是$\angle HAD$平分线,⑤**证毕**
|
|
|
|
|
|
$\therefore \triangle ADF \cong \triangle AHF$
|
|
|
⑦ **证毕**
|
|
|
|
|
|
---
|
|
|
|
|
|
|
|
|
|
|
|
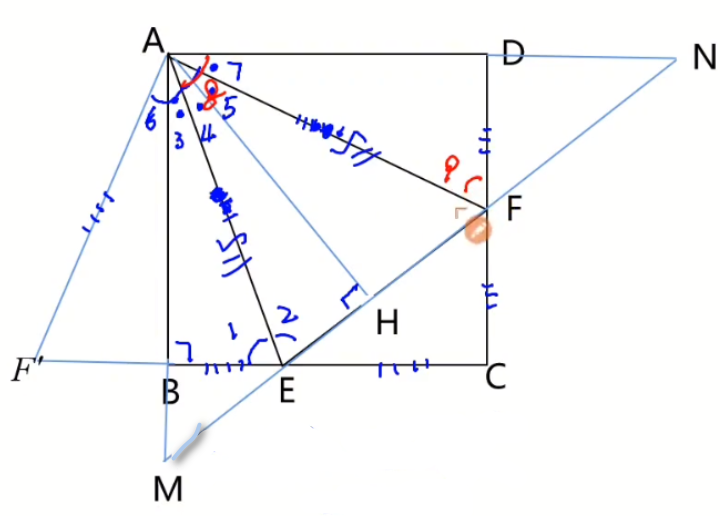
求证:$MA=MF$
|
|
|
|
|
|
因为$\angle 1=\angle 2$ 已经证明的全等三角形
|
|
|
$\angle 1=\angle 8$ 平行边内错角相等
|
|
|
$\therefore \angle 2=\angle 8$
|
|
|
$\triangle ANE$是等腰三角形,$AN=NE$ ⑨ **证毕**
|
|
|
|
|
|
$\because \triangle AHF \cong \triangle ADF$
|
|
|
$\therefore \angle HFA=\angle 9$
|
|
|
|
|
|
$\because \angle 9=\angle MAF$ 平行线内错角相等
|
|
|
|
|
|
$\therefore \angle HFA=\angle MAF$
|
|
|
|
|
|
所以$\triangle MAF$是一个等腰三角形
|
|
|
$\therefore MF=MA$ ⑧**证比**
|
|
|
|
|
|
⑩ 一看就是 $12345$模型了,因为$tan \alpha=\frac{1}{2},\alpha+\beta=45^{\circ}$
|
|
|
$\therefore tan \beta=\frac{1}{3}$
|
|
|
**证毕**,忘记怎么证明的时候,回去复习一下 $12345$模型即可。 |