You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
1.2 KiB
1.2 KiB
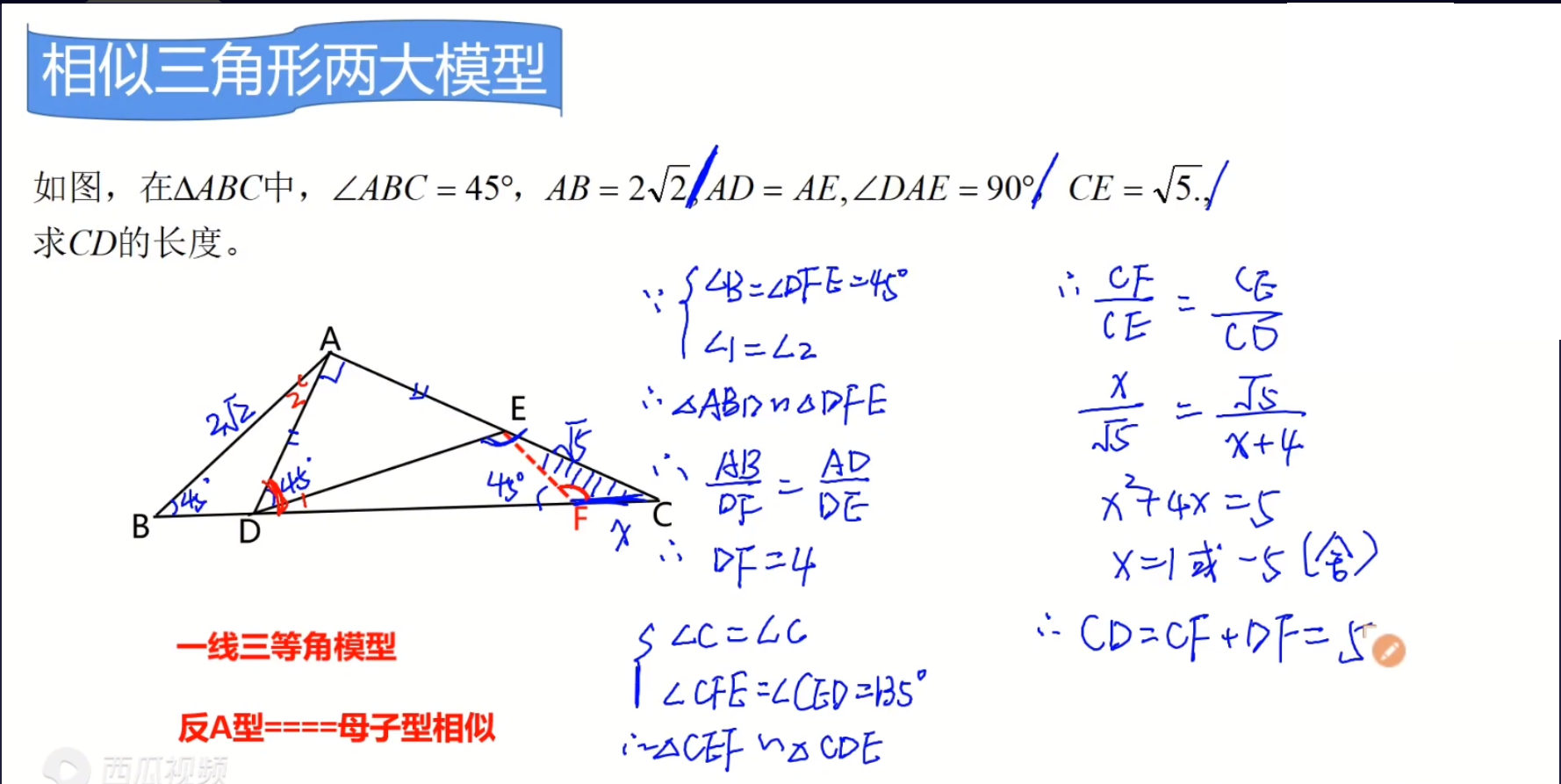
分析题意:
\because \angle ADC=45^{\circ}+\angle 1
\because \angle ADC=45^{\circ}+\angle 2
\therefore \angle 1=\angle 2
此时,构造相似三角形,通过比例关系解题就是 关键
因为\angle 1在\triangle EDC中,同时知道EC长度为\sqrt{5},我们需要构造出一个和 \triangle ABD相似的三角形,所以过E引EF交CD于F,使得\angle EFD=45^{\circ}
则\triangle EDF \sim \triangle ABD
\therefore \frac{AD}{AB}=\frac{DE}{FD}
\because DE=\sqrt{2} AD
\therefore FD=\sqrt{2}AB=\sqrt{2}*2\sqrt{2}=4
算出DF后,下面需要继续求解FC,才能算出CD的长度。
继续观察发现,
\left\{\begin{matrix}
\angle C=\angle C & \\
\angle CFE=135^{\circ} & \\
\angle CDE=135^{\circ} &
\end{matrix}\right.
\therefore \triangle CEF \sim \triangle CDE
设CF=x
\therefore \frac{x}{CE}=\frac{CE}{CD}
x^2+4x=5
解方程:x_1=1,x_2=-5,因为x>0,x_2=-5舍掉,最终x=1,所以CD=4+1=5