You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
This file contains ambiguous Unicode characters that may be confused with others in your current locale. If your use case is intentional and legitimate, you can safely ignore this warning. Use the Escape button to highlight these characters.

(1)
将三个点代入方程,求解方程组
$$
\large \left\{\begin{matrix}
0=a(-1)^2-b+c & \\
0=9a+3b+c & \\
c=-3
\end{matrix}\right.
$$
整理:
$$
\large \left\{\begin{matrix}
a-b-3=0 & \\
3a+b-1=0 & \\
c=-3
\end{matrix}\right.
$$
$$ \Rightarrow
\large \left\{\begin{matrix}
a=1& \\
b=-2& \\
c=-3
\end{matrix}\right.
$$
即$y=x^2-2x-3$
顶点$D$的坐标,根据顶点坐标公式:
$$
\large \left\{\begin{matrix}
x=-\frac{b}{2a} & \\
y=\frac{4ac-b^2}{4a} &
\end{matrix}\right.
$$
$$ \Rightarrow
\large \left\{\begin{matrix}
x=1 & \\
y=-4 &
\end{matrix}\right.
$$
---
** 重点是第二问**:
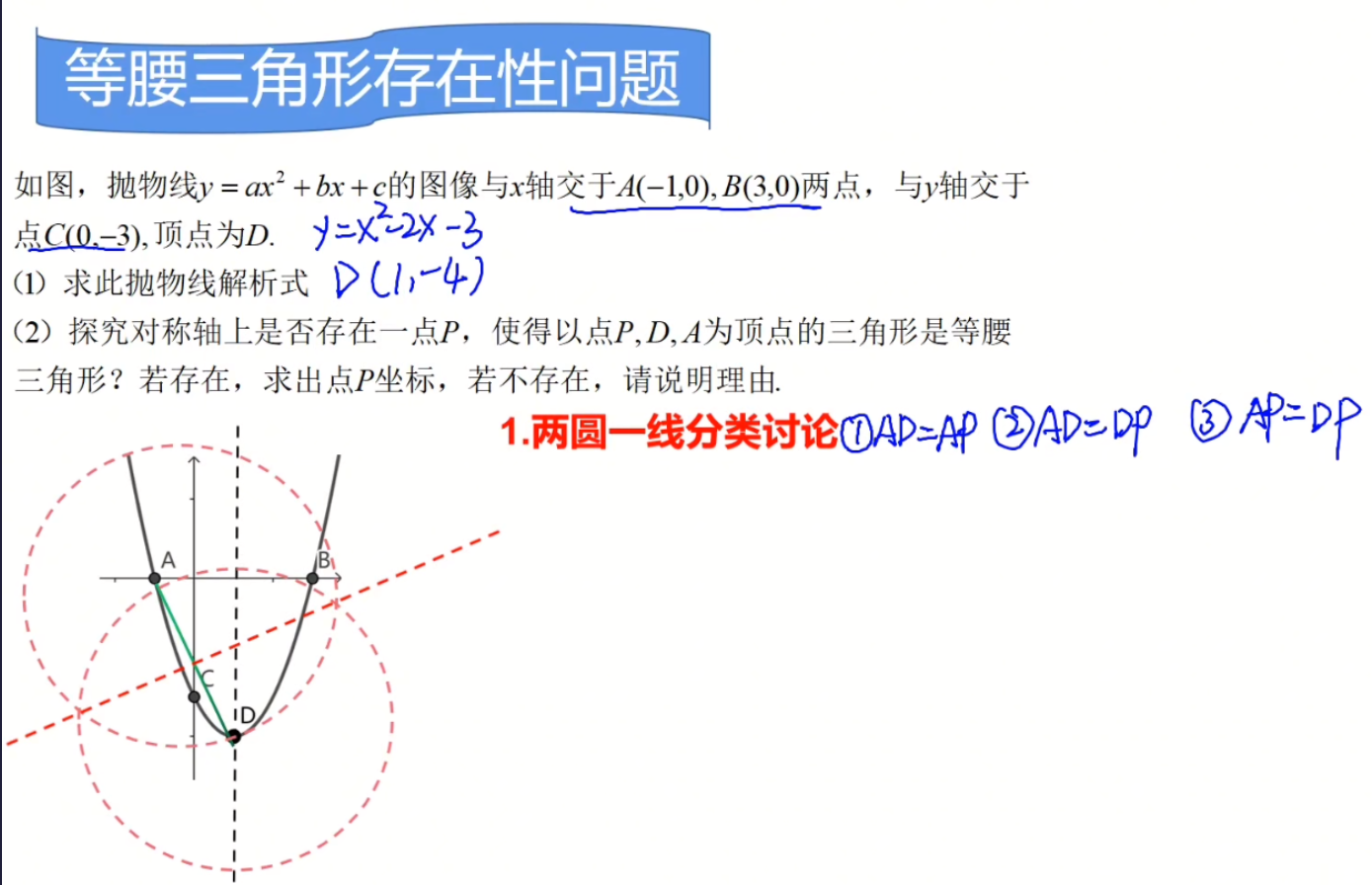
因为是等腰三角形的情况共三种,需要分情况讨论:
- $AD=AP$ 在以$A$为圆心,以$AD$长为半径的圆对称轴的交点上
- $AD=DP$ 在以$D$为圆心,以$AD$长为半径的圆对称轴的交点上
- $AP=DP$ 在$AD$垂直平分线与对称轴的交点上
有两种方法,几何法和代数法,分别来计算一下:
#### 几何法
- $AD=AP$ 时,$P$点坐标就是$D$关于$X$轴的对称点,$P(1,4)$
- $AD=DP$ 时,利用勾股定理,可以求解$AD$长度,也就是$DP$长度=$\sqrt{(-1-1)^2+(-4)^2}=2\sqrt{5}$,$P_2=({-1,2\sqrt{5}-4})$
< font color = 'red' size = 4 >< b > 注意</ b ></ font >
这里非常容易丢失一组解!也可能是以$D$为圆心的圆与对称轴的下方交点! 即$P_3=(-4-2\sqrt{5})$
垂直平分线的交点:
此时$AP=PD$
设 上面一小段为$m$
$(4-m)^2=m^2+2^2 \Rightarrow $
$16-8m+m^2=m^2+4$
$m=\frac{3}{2}$
$P_4(1,-\frac{3}{2})$
#### 代数法
- 表示点
$A(-1,0),D(1,-4),P(1,t)$
- 表示边
利用两点间距离公式 $\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$
分别计算$AD^2,AP^2,DP^2$,就可以免去开根号了
- 列方程求解
$AD^2=4+16=20$
$AP^2=4+t^2$
$DP^2=(t+4)^2$
三个方程式分别联立成三个方程组:
$$
\large \left\{\begin{matrix}
4+t^2=20 & ① \\
4+t^2=t^2+8t+16 & ② \\
(t+4)^2=20 & ③
\end{matrix}\right.
$$
① $t=4$ (根据题意舍掉$-4$)
② $t=-\frac{3}{2}$
③ $t=\pm2\sqrt{5}-4$