4.1 KiB
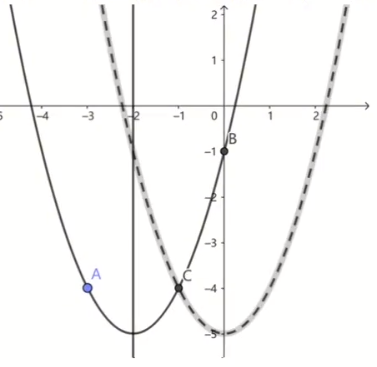
(1) 将两点代入方程求解方程组即可:
\left\{\begin{matrix}
-4=(-3)^2-3b+c & \\
-1=c &
\end{matrix}\right.
\therefore b=4,c=-1,二次函数方程:y=x^2+4x-1
下面来求一下直线方程:
y=kx+b
\large \left\{\begin{matrix}
-4=k(-3)+b & \\
-1=b &
\end{matrix}\right.
解得:k=1,b=-1,直线方程y=x-1
(2)铅垂法+二次方程求顶点+校验
由动点P向x轴引一条平等于y轴的直线，交AB于M,则S_{\triangle ABP}=S_{\triangle APM}+S_{\triangle BPM}
P的坐标是设未知数x=m,然后通过二次函数获取到的y=m^2+4m-1M的坐标是通过直线方程求出的，将x=m代入直线方程，可得y=m-1
S=\frac{1}{2} PM * (A横坐标 -B横坐标)
=\frac{1}{2}(m-1-(m^2+4m-1))*(0-(-3))
=-\frac{3}{2}m^2-\frac{9}{2}m
\because -\frac{3}{2}<0，同一个开口向下的抛物线，所以函数有最大值，最大值在顶点，
X=-\frac{b}{2a}=-\frac{-\frac{9}{2}}{-3}
解得X=-\frac{3}{2}时，取得最大值，最大值
=\frac{4ac-b^2}{4a}=\frac{0-\frac{81}{4}}{-6}=\frac{81}{24}=\frac{27}{8}
(3) 前导知识:抛物线平移
填空题：
将抛物线y=-x^2向右平移一个单位，所得函数解析式为( y=-(x-1)^2 )
分析：直接根据 左加右减 的原则进行解答即可． 考点: 二次函数图象与几何变换．
所以，右移两个单位，新方程就是y=(x-2)^2+4(x-2)-1
y=x^2-4x+4+4x-8-1
y=x^2-5
由于点C是两个抛物线的交点，所以就是联立两个方程：
\large \left\{\begin{matrix}
y=x^2+4x-1 & \\
y=x^2-5 &
\end{matrix}\right.
\therefore C(-1,-4)
- 由于
D是原抛物线对称轴上一点,所以横坐标已知，为-2,纵坐标不知道，设为t,则D(-2,t) - 设
E点坐标为(m,n)
现在想要知道，是不是存一个菱形BCDE
步骤：
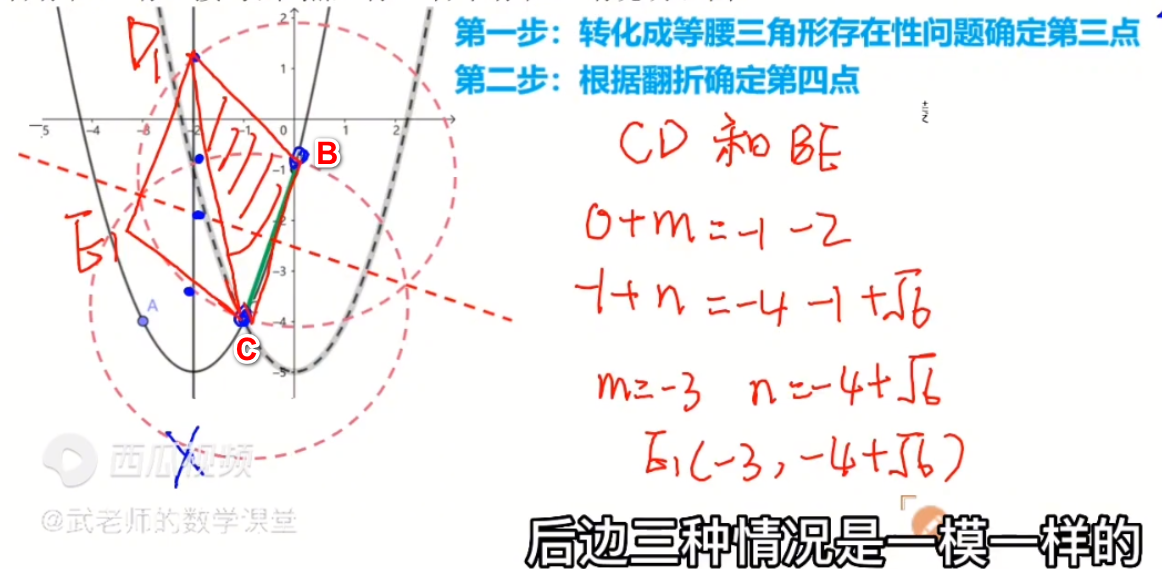
- 转化为等腰三角形存在性问题确定第三点
- 根据翻折确定第四点
解释：因为菱形的四条边都相等，当一条边的两个点确定的时候，只要找出的第三点能够构成等腰三角形，这个点就是菱形的第三点。
另外，只要等腰三角形确定，就可以通过翻折找出对应的菱形。
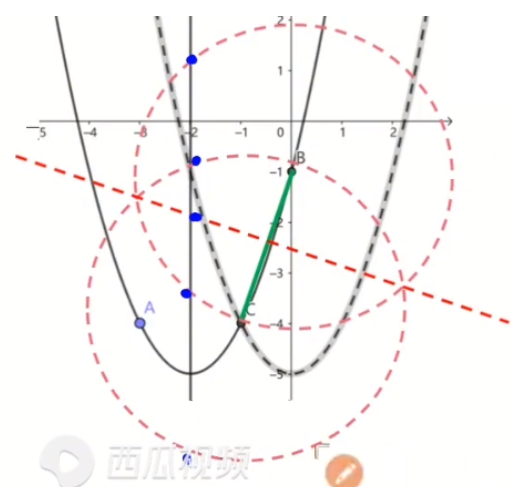
BC的等腰三角形存在性问题，就是在两圆一线上！
另外，D点要求在原抛物线的对称轴上，所以图中的蓝色点都是可能的答案。
坑：
最下方的圆与原抛物线对称轴交点的蓝色点(西瓜视频字里面那个半蓝色的点)需要舍掉，原因是经过验证，此点与B,C三点共线，无法组成三角形，不符合要求，舍掉。
代数法求解坐标：
(1)确定点坐标，不知道的用变量描述
(2)等腰就是两条边的欧几里得距离相等，这里直接取平方计算，方便。
(3)平方两两相等，就可以得到5个点的坐标，再通过上面的分析，舍掉最后一个点，得到四个点的坐标
最后一步，开始翻折解决问题：
因为菱形就是一个平行四边形，有相应的规律：
这条对角线的坐标相加，等于，另一条对角线的坐标相加
C(-1,-4),D坐标上面求出了，B(0,-1),E(m,n)
X_D+X_C=X_B+X_E
-2-1=0+m
m=-3
Y_D+Y_C=Y_B+Y_E
-1+\sqrt{6}-4=-1+n
n=-4+\sqrt{6}
\therefore M_1(-3,-4+\sqrt{6})
同理，解得
M_2(-3,-4-\sqrt{6})
M_3(-1,2)
M_4(1,-3)