You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
36 lines
1.4 KiB
36 lines
1.4 KiB
|
|
|
|
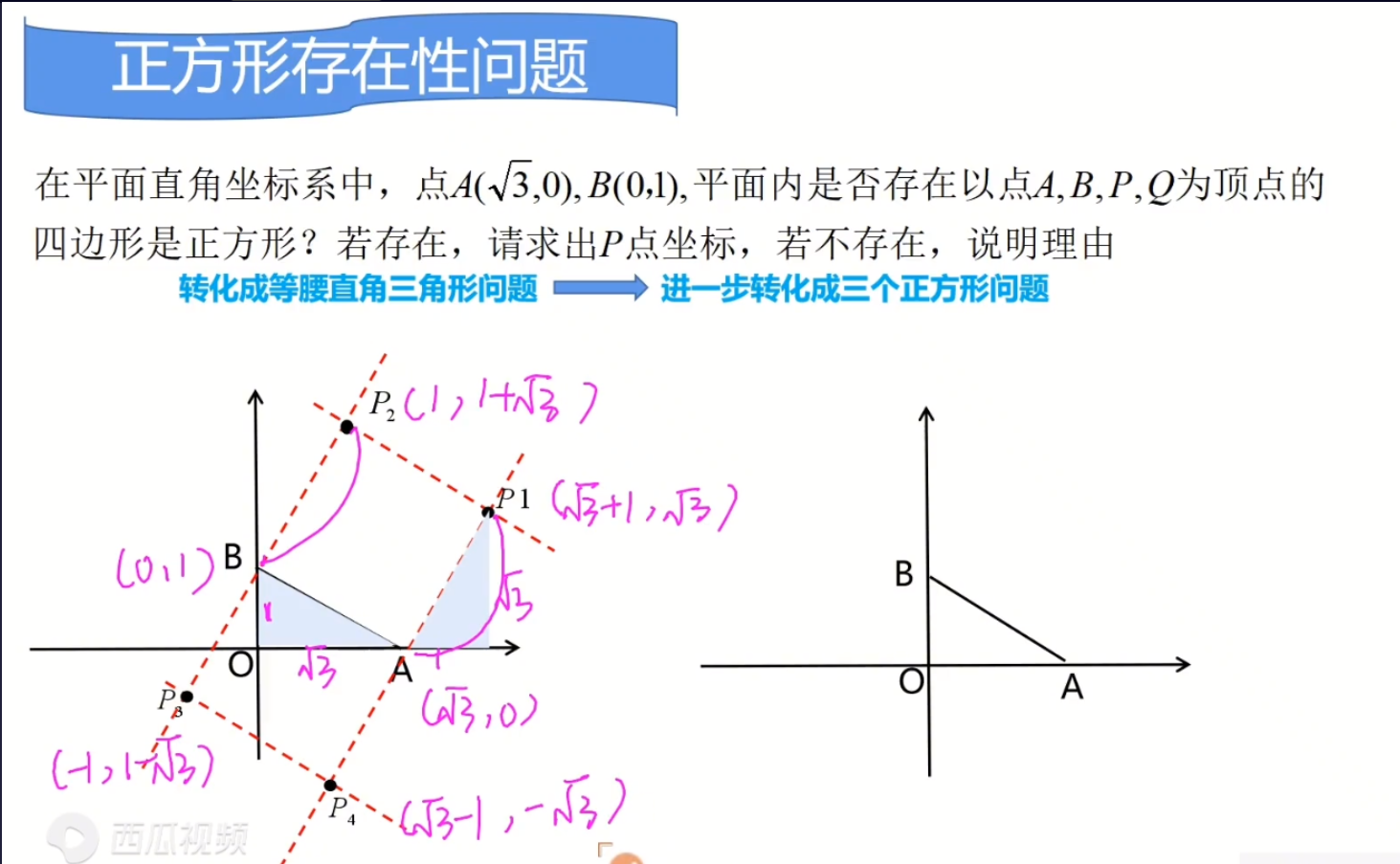
- 如果$AB$是边
|
|
- 通过$A,B$引$AB$的垂线,再分别截取$AB$的长度,就可以构造正方形。
|
|
- 因为图中的$P,Q$没有说具体位置,所以$P_1,P_2,P_3,P_4$都可能是答案。
|
|
- 以$P_1$为例进行计算:
|
|
通过三角形全等,$P_1(\sqrt{3}+1,\sqrt{3})$
|
|
其中的三个点,就不用这么麻烦了,利用平移思想就可以得到了:
|
|
对照$A->P_1$,$B->P_2$,$A$是$+1,+\sqrt{3}$
|
|
$B$也是$+1,+\sqrt{3}$,即$P_2(1,1+\sqrt{3})$
|
|
同理$P_3(-1,1-\sqrt{3})$
|
|
$P_4(\sqrt{3}-1,-\sqrt{3})$
|
|
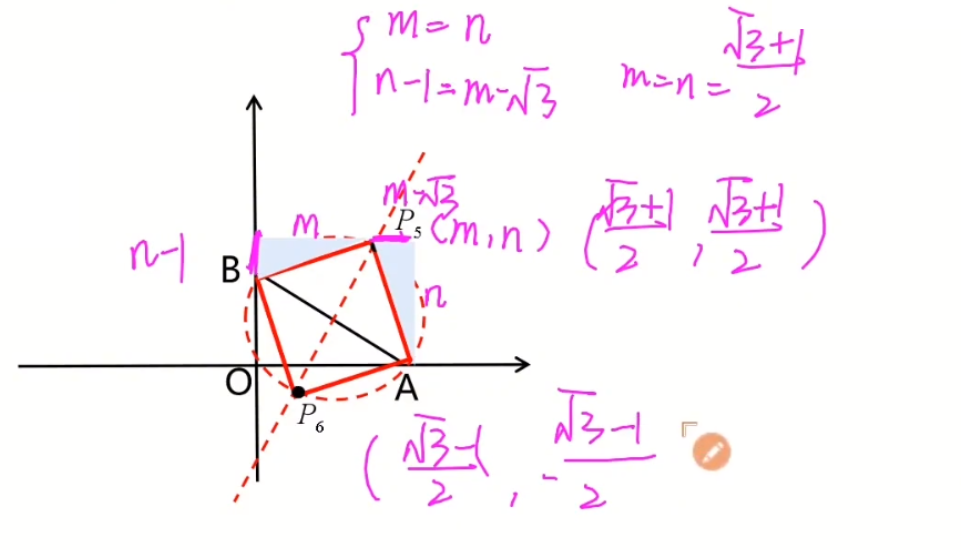
- 如果$AB$是对角线
|
|
|
|
|
|
则以$AB$为对角线的正方形必然在图中的圆上。
|
|
设$P_5$坐标为$(m,n)$,利用全等三角形,知道
|
|
|
|
$$
|
|
\large \left\{\begin{matrix}
|
|
m=n & \\
|
|
n-1=\sqrt{3}-m &
|
|
\end{matrix}\right.
|
|
$$
|
|
<font color='red' size=4><b>注:上面的板书写错了,是$n-1=\sqrt{3}-m$</b></font>
|
|
$\therefore m=n=\frac{\sqrt{3}+1}{2}$
|
|
即$P_5(\frac{\sqrt{3}+1}{2},\frac{\sqrt{3}+1}{2})$
|
|
|
|
那$P_6$怎么求呢?
|
|
还是中线定理:
|
|
$x+\frac{\sqrt{3}+1}{2}=\sqrt{3}$
|
|
$y+\frac{\sqrt{3}+1}{2}=1$
|
|
|
|
解得:
|
|
$x=\frac{\sqrt{3}-1}{2}$
|
|
$y=-\frac{\sqrt{3}-1}{2}$ |