You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
60 lines
2.0 KiB
60 lines
2.0 KiB

|
|
|
|
#### 题目解析
|
|
|
|
第一问比较简单,说是用 待定系数法,将已知点坐标代入到二次函数方程和直线方程,然后联立方程组求解即可:
|
|
|
|
$$
|
|
\large \left\{\begin{matrix}
|
|
0=-1-b+c & \\
|
|
3=-4+2b+c &
|
|
\end{matrix}\right.
|
|
$$
|
|
|
|
$\therefore b=2,c=3$
|
|
即抛物线方程$y=-x^2+2x+3$
|
|
|
|
直线方程$y=kx+b $
|
|
$$
|
|
\large \left\{\begin{matrix}
|
|
0=-k+b & \\
|
|
3=2k+b &
|
|
\end{matrix}\right.
|
|
$$
|
|
$\therefore b=1,k=1$
|
|
直线方程就是$y=x+1$
|
|
|
|
**直接求出$D$点坐标**
|
|
|
|
直接利用 **顶点坐标公式**:
|
|
$$
|
|
\large \left\{\begin{matrix}
|
|
x=-\frac{b}{2a} & \\
|
|
y=\frac{4ac-b^2}{4a} &
|
|
\end{matrix}\right.
|
|
$$
|
|
将$a,b$代入即可求出
|
|
$x=1,y=4$
|
|
|
|
**重点是第$2$问**
|
|
|
|
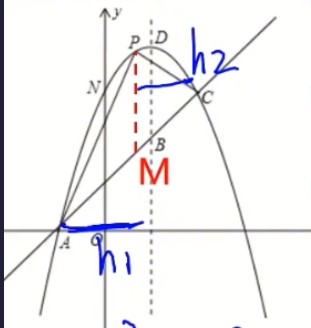
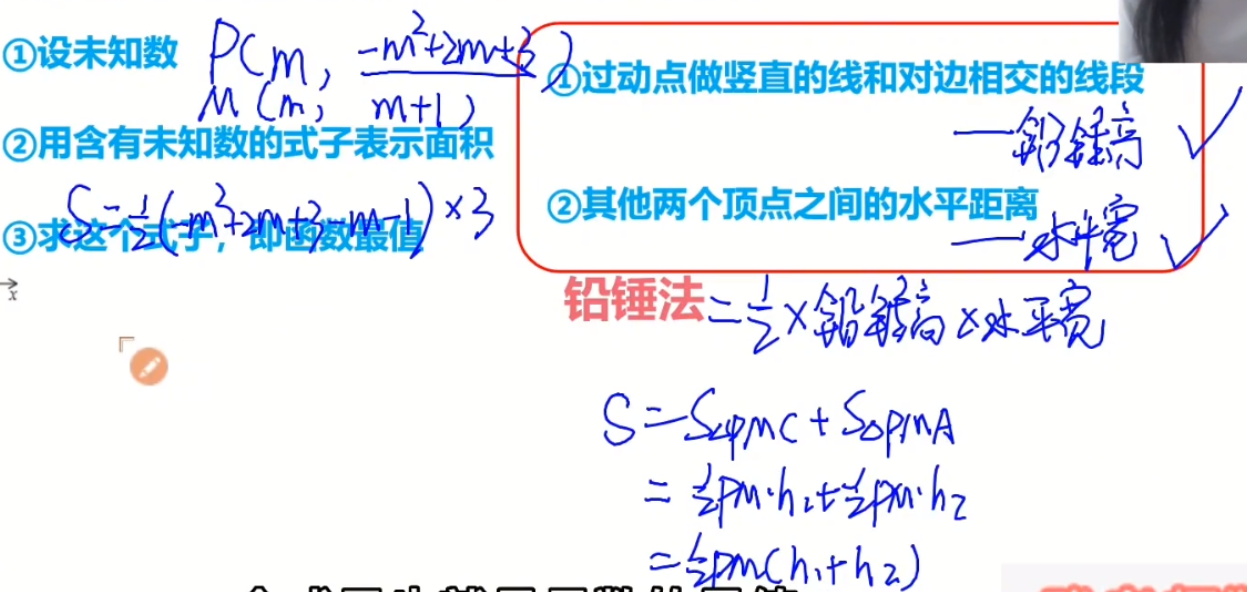
在抛物线上的动点求面积最大值,使用的办法是 **铅垂法**
|
|
|
|
就是由动点$P$向$x$轴引出一条平行于$y$轴的垂线,与直线$AC$相交,设交点为$M$
|
|
|
|
$\therefore S_{\triangle PAC}=S_{\triangle PAM}+S_{\triangle PMC} $
|
|
|
|
|
|
|
|
|
|
- $P$的坐标是设未知数$x=m$,然后通过二次函数获取到的$y=-m^2+2m+3$
|
|
- $M$的坐标是通过直线方程求出的,将$x=m$代入直线方程,可得$y=m+1$
|
|
|
|
$S=\frac{1}{2} PM * (C横坐标 -A横坐标)$
|
|
$=\frac{1}{2}(-m^2+2m+3-m-1)*(2-(-1))$
|
|
$=(-\frac{1}{2}m^2+\frac{1}{2}m+1)*3$
|
|
$=-\frac{3}{2}(m^2-m-2)$
|
|
$=-\frac{3}{2}(m-\frac{1}{2})^2+\frac{27}{8}$ **配方法**
|
|
$\therefore m=\frac{1}{2}$时,$S$最大,最大值是$\frac{27}{8}$
|
|
|
|
最后不要忘记检验,因为题目中说了,动点$P$是在$AC$上方的,所以$M$需要在$-1,2$之间。现在$m=\frac{1}{2}$是在$(-1,2)$之间的,符合要求,答案就是$\frac{27}{8}$ |