You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
25 lines
1.1 KiB
25 lines
1.1 KiB
|
|
|
|
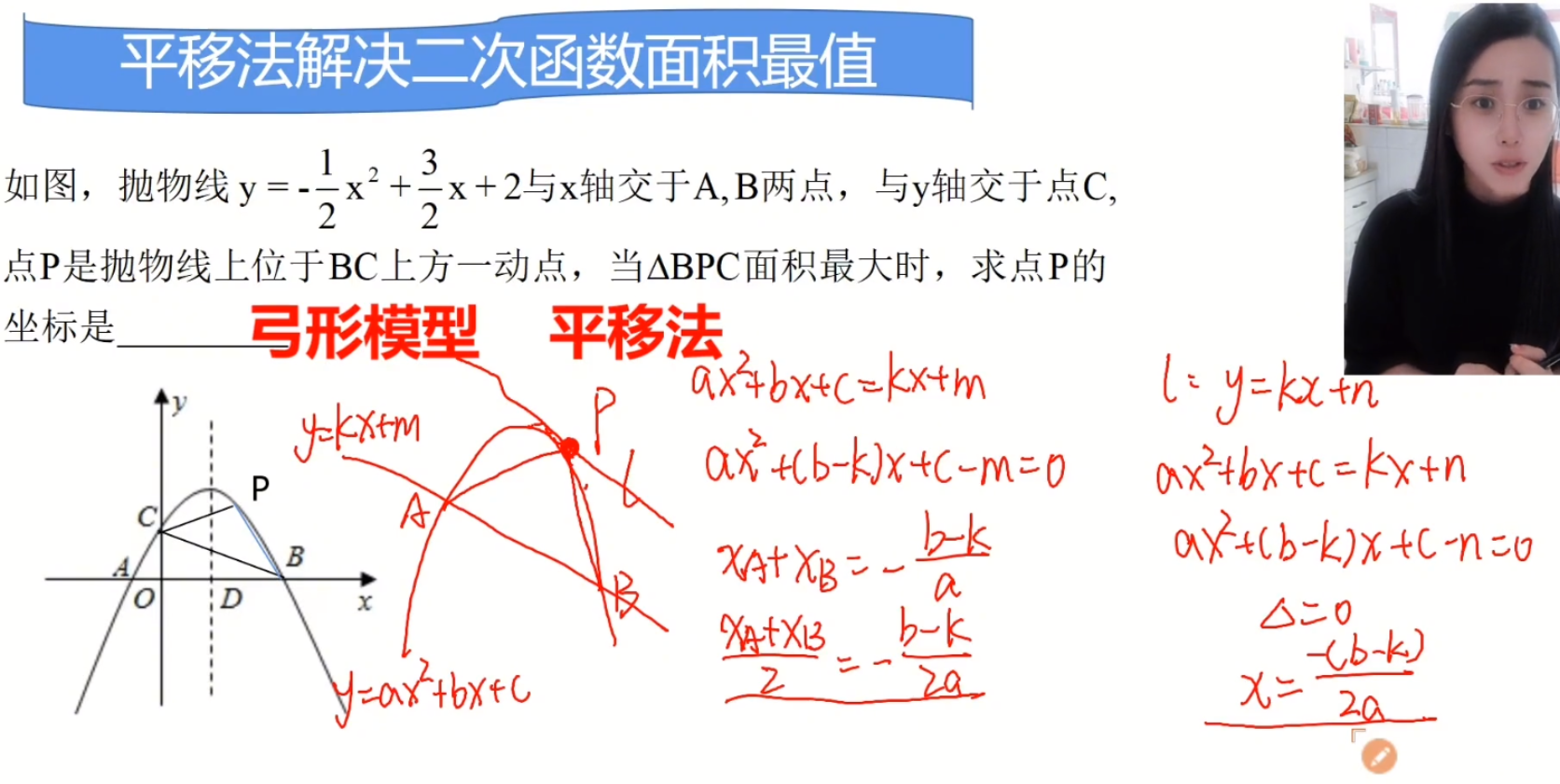
**弓形模型的证明**
|
|
设二次函数为$y=ax^2+bx+c$
|
|
直线方程为$y=kx+m$
|
|
|
|
联立两个方程解出$A,B$的中点$X$坐标
|
|
|
|
$ax^2+bx+c=kx+m$
|
|
$ax^2+(b-k)x+c-m=0$
|
|
这里不用真的求出$x1,x2$的值,而是想要求解$\frac{x_1+x_2}{2}$
|
|
所以利用韦达定理,得到$\frac{x_1+x_2}{2}=-\frac{b-k}{2a}$
|
|
|
|
现在来思考$P$在什么位置情况下,使得$S_{\triangle PAB}$面积最大。
|
|
|
|
想要使三角形面积最大,因$AB$所以边长固定,就是要求从$P$向$AB$引出的高最大就是三角形面积最大。
|
|
将直线$AB$向抛物线外平移,当与抛物线只有一个交点时,为边界位置,再往外走,就与抛物线无关了。
|
|
设此方程为$y=kx+n$(因为斜率与$y=kx+m$一样,平行关系)
|
|
根据交点,就是联立两个方程$ax^2+bx+c=kx+n$
|
|
$ax^2+(b-k)x+c-n=0$
|
|
此时此方程只有一个交点解,即$\triangle=\sqrt{b^2-4ac}=0$
|
|
|
|
$x=\frac{(k-b) \pm \triangle }{2a}=\frac{k-b}{2a}$
|
|
|
|
结论:两个值是一样滴,**问题得证** |