## [$AcWing ~ 2$ $01$背包](https://www.acwing.com/problem/content/description/2/) ### 一、知识架构 - **$01$背包** $N$个物品，容量$V$的背包(上限)，$w_i$表示物品的体积,$v_i$表示价值 如何组装背包，在$V$的上限限制情况下，使得价值最大,求最大值。 **总结：每个物品只有$1$个，可以选或不选，求在容量限制下的价值最大值。** - **完全背包** 每个物品有无限个，求价值最大是多少。 - **多重背包** 每个物品个数不一样，不是无限，也不是只有一个，有$k_i$的个数限制。 多重背包有一个二进制优化的扩展，称为 **多重背包II** ,就是打包策略。 - **分组背包** 物品有$n$组，各一组有若干个。每一组最多选择一个物品，比如水果组选择了苹果，就不能选香蕉。 - **混合背包** 物品一共有三类： 第一类物品只能用$1$次（$01$背包）； 第二类物品可以用无限次（完全背包）； 第三类物品最多只能用 $s_i$ 次（多重背包）； **注意：不一定要装满背包** ### 二、01背包的递归表示 ![](https://img2020.cnblogs.com/blog/8562/202110/8562-20211007092633901-1608550701.png) ```cpp {.line-numbers} #include using namespace std; const int N = 1010; int n, m; int w[N], v[N]; int res; void dfs(int u, int r, int s) { if (u == n + 1) { res = max(res, s); return; } if (v[u] <= r) dfs(u + 1, r - v[u], s + w[u]); dfs(u + 1, r, s); } int main() { cin >> n >> m; for (int i = 1; i <= n; i++) cin >> v[i] >> w[i]; dfs(1, m, 0); printf("%d\n", res); return 0; } ``` 递归表示法的缺点： 因为有大量的重复计算，所以，不出意外的在大数据量的情况下，$TLE$了！我们需要找一个办法进行优化。 ### 三、记忆化搜索 ```cpp {.line-numbers} #include using namespace std; const int N = 1010; int n, m; int w[N], v[N]; int f[N][N]; int dfs(int u, int r) { if (~f[u][r]) return f[u][r]; if (u == n + 1) return 0; if (v[u] <= r) return f[u][r] = max(dfs(u + 1, r), dfs(u + 1, r - v[u]) + w[u]); return f[u][r] = dfs(u + 1, r); } int main() { memset(f, -1, sizeof f); cin >> n >> m; for (int i = 1; i <= n; i++) cin >> v[i] >> w[i]; printf("%d\n", dfs(1, m)); return 0; } ``` $Q$:为什么记忆化搜索要以$int$返回，使用以前习惯的$void$返回不行吗？ 让你失望了，如果$dfs$采用$void$作为返回值，是无法使用记忆化的： 因为我们利用每一次搜索的 结果进而达到记忆化：之前搜过的就不用再搜了。 普通搜索的低效使得很多时候在数据比较大时会导致$TLE$，一个重要原因是其搜索过程中重复计算了重叠子问题。记忆化搜索以搜索的形式加上动态规划的思想，面对会有很多重复计算的问题时，在搜索过程中记录一些状态的答案，可以减少重复搜索量。记忆化搜索本质上是$DP$，它们都保存了中间结果，不同点是$DP$从下往上算，记忆化$dfs$因为是递归所以从上往下算。 #### 记忆化搜索 * 递归函数的结果以返回值形式存在，不能以全局变量或参数形式传递 * 不依赖任何外部变量 （根据以上两个要求把朴素暴搜$dfs$写出来后，添加个记忆化数组就$ok$了） 记忆化数组一般初始化为$-1$。在每一状态搜索的开始进行判断，如果该状态已经计算过，则直接返回答案，否则正常搜索。 * 函数的参数表达的是： 状态 * 函数的返回值表达的是:结果 策略与办法 如果对记忆化搜索不熟练，可以先写出$void$型$dfs$，再转化为有返回值的$dfs$，最后再加个数组记录已经搜过的状态就是记忆化$dfs$了。 ### 四、二维数组法 ```cpp {.line-numbers} #include using namespace std; const int N = 1010; int n, m; int f[N][N]; int main() { cin >> n >> m; for (int i = 1; i <= n; i++) { int v, w; cin >> v >> w; for (int j = 1; j <= m; j++) { f[i][j] = f[i - 1][j]; if (j >= v) f[i][j] = max(f[i][j], f[i - 1][j - v] + w); // 两种情况取最大值 } } printf("%d\n", f[n][m]); return 0; } ``` ### 五、一维数组法 为什么要用一维数组优化$01$背包问题 因为我们看到上面的存储方式，其实第$i$件物品选择或不选择两种方式，都只和$i-1$时的情况相关联，也就是说在$i-1$再以前的状态和数据与$i$无关，换句话说，就是没啥用了，可以清除掉了。这样一路走一路依赖它前面一行就OK，可以把二维数组优化为一维。 那么，怎么个优化法呢？答案是用一个一维数组。 **这里最核心的问题是为什么容量的遍历要从大到小，和上面二维的不一样了呢？？** 这是因为第$i$个要依赖于第$i-1$个，如果从小到大，那么$i-1$先变化了，而$i$说的依赖于$i-1$，其实是在没变化前的$i-1$ 信息，这么直接来就错了。那怎么才能对呢？就是从大到小反向遍历，这样$i-1$都是以前的信息，还没变，就$OK$了！有点绕啊，但还算好理解！ ```cpp {.line-numbers} #include using namespace std; const int N = 1010; int n, m; int f[N]; int main() { cin >> n >> m; // 01背包模板 for (int i = 1; i <= n; i++) { int v, w; cin >> v >> w; for (int j = m; j >= v; j--) f[j] = max(f[j], f[j - v] + w); } printf("%d\n", f[m]); return 0; } ``` ### 七、$01$背包之恰好装满【扩展】 有$n$个体积和价值分别为$v_i$,$w_i$的物品，现从这些物品中挑选出总体积 恰好 为 $m$ 的物品，求所有方案中价值总和的最大值。 **输入**：包含多组测试用例，每一例的开头为两位整数 $n、m$,$(1<=n<=10000,1<=m<=1000)$，接下来有 $n$ 行，每一行有两位整数 $v_i、w_i(1<=v_i<=10000,1<=w_i<=100)$。 **输出**：为一行，即所有方案中价值总和的最大值。若不存在刚好填满的情况，输出$-1$。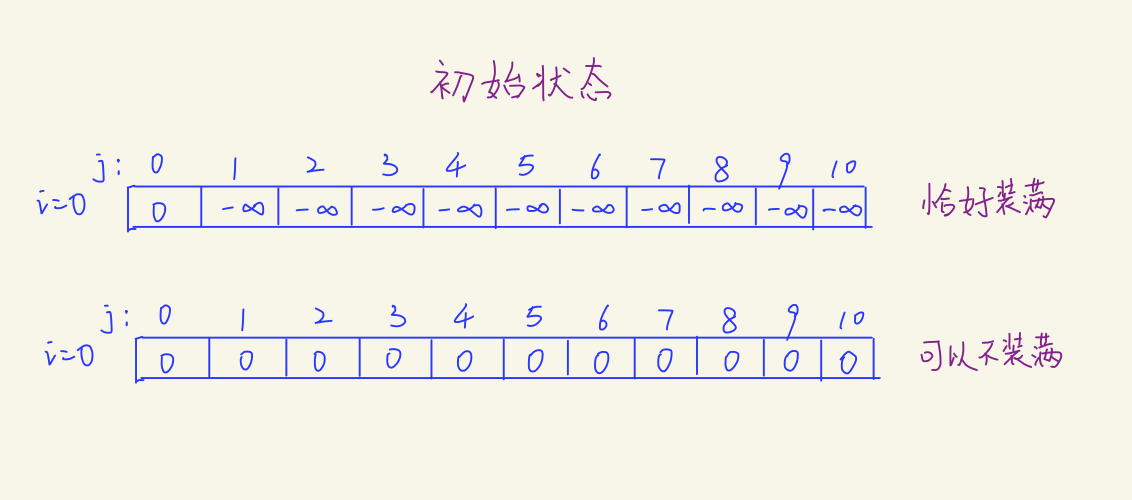 测试用例： ```c++ 3 4 1 2 2 5 2 1 3 4 1 2 2 5 5 1 ``` 答案： ```c++ 6 -1 ``` 恰好装满： * 求最大值时，除了$f[0]$为$0$，其他都初始化为无穷小 `-0x3f3f3f3f` * 求最小值时，除了$f[0]$为$0$，其他都初始化为无穷大 `0x3f3f3f3f` 不必恰好装满： 全初始化为$0$ ![2.jpeg](https://cdn.acwing.com/media/article/image/2021/03/10/64630_c67d338f81-2.jpeg) #### $Q:$为什么这样设置？ 背包没恰好装满是无效状态， 恰好装满是有效状态。 当背包的状态为无效状态时，$f[i]$的值是$-INF$，这样就可以从状态转移矩阵中区分出有效状态和无效状态了。 回顾一下状态转移实现过程： ```cpp {.line-numbers} for (int j = 1; j <= m; j++) { f[i][j] = f[i - 1][j]; if (j >= v) f[i][j] = max(f[i][j], f[i - 1][j - v] + w); //两种情况取最大值 } ``` $f[i][j]$ 的值是由 $f[i - 1][j]，f[i - 1][j - w]$来推导出来的，也就是 $f[i][j]$ 的取值 只与前面的状态有关系,所有的状态都是从以前的状态来推导出来的。换句话说，所有的**有效状态**是从之前的**有效状态**和**无效状态**推导出来的！！！ 目标： 通过初始化无效状态为$-INF$,在不改变原来代码的情况下，解决掉恰好装满的问题！ 我们来分析一下有效状态与无效状态之间的转化关系： 先上结论：
| 前序状态$f[i - 1][j]$ | 前序状态$f[i - 1][j - w]$ | 当前状态$f[i][j]$ | 转移来源 | | ----------------------------------------------------- | ----------------------------------------------------- | ----------------------------------------------------- | -------------------------------------------------------------------------------------------------------------------------------------------------- | | 有效状态(满) | 有效状态(满) | 有效状态(满) | $max(f[i-1][j],f[i-1][j-w]+v)$ | | 无效状态(不满) | 有效状态(满) | 有效状态(满) | $max(f[i-1][j-w]+v,-INF)$ | | 有效状态(满) | 无效状态(不满) | 有效状态(满) | $max(f[i-1][j],-INF)$ | | 无效状态(不满) | 无效状态(不满) | 无效状态(不满) | 转不过来了
$f[i][j] = max(f[i-1][j], f[i - 1][j - w] + v)$,$-INF$会被加上$v$,不再是$-INF$,但肯定是负数。 |
#### 无效状态的处理方法 上面表格中也提到了这个问题：$f[i][j] = max(f[i][j], f[i - 1][j - v] + w)$,如果两个前序状态都是无效状态，那么$-INF$会被加上$w$,不再是$-INF$,但肯定是负数。在最终结果判定中，我们可以认为是负数的，就是无效状态：**假设负无穷不是靠你简单加上几个小正数就能大于零的**~ #### 二维代码实现 ```cpp {.line-numbers} #include using namespace std; const int N = 10010; int n, m, f[N][N]; int main() { // 文件输入 freopen("2_QiaHaoFill.in", "r", stdin); while (cin >> n >> m) { memset(f, -0x3f, sizeof(f)); // 其它位置全部初始化为-INF for (int i = 0; i < N; i++) f[i][0] = 0; // 第一列初始化为0 for (int i = 1; i <= n; i++) { int w, v; cin >> v >> w; for (int j = v; j <= m; j++) f[i][j] = max(f[i][j], f[i - 1][j - v] + w); } if (f[n][m] < 0) puts("-1"); else printf("%d\n", f[n][m]); } return 0; } ``` #### 一维代码实现 ```cpp {.line-numbers} #include using namespace std; const int N = 10010; int n, m, f[N]; int main() { // 文件输入 freopen("2_QiaHaoFill.in", "r", stdin); while (cin >> n >> m) { memset(f, -0x3f, sizeof(f)); f[0] = 0; for (int i = 1; i <= n; ++i) { int v, w; cin >> v >> w; for (int j = m; j >= v; j--) f[j] = max(f[j], f[j - v] + w); } if (f[m] < 0) puts("-1"); else printf("%d\n", f[m]); } return 0; } ```