## 模型
给定一张包含 $n$ 个点和 $m$ 条边的 **无向图**,再给定 $q$ 个询问:$a_i,L_i$,判断是否存在一条从$1$号点走到$a_i$号点的恰好经过$L$条边的路径。
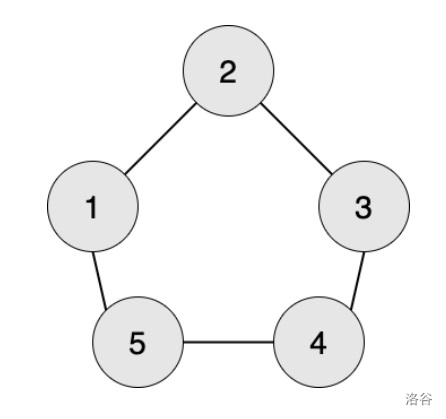 设求第$3$点为第$3$阶段时,点$1$是否需要提供原材料。
$【3,3】 => 【2,2】,【4,2】$
$【2,2】 => 【1,1】,【3,1】$
$【4,2】 => 【3,1】,【5,1】$
$【1,1】 => 【2,0】,【5,0】$
$【3,1】 => 【2,0】,【4,0】$
$【5,1】 => 【1,0】,【4,0】$ # 此处$1$需要提供原材料
比较容易想到对于每个询问进行暴搜,若点$1$为$0$,则$Yes$
时间复杂度很高,必然超时。
```cpp {.line-numbers}
#include
using namespace std;
typedef pair PII;
#define x first
#define y second
const int N = 1e5 + 10, M = N << 1;
// 20个测试点,过了7个,得了35分,其它TLE
// 邻接表
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool bfs(int start, int dist) {
queue q;
q.push({start, dist});
while (q.size()) {
auto u = q.front();
q.pop();
if (u.x == 1 && u.y == 0) return true; // 在用完所有步数后,到达1号点,成功!
for (int i = h[u.x]; ~i; i = ne[i]) {
int v = e[i];
if (u.y) q.push({v, u.y - 1});
}
}
return false;
}
int main() {
memset(h, -1, sizeof h);
int n, m, Q;
cin >> n >> m >> Q;
while (m--) {
int a, b;
cin >> a >> b;
add(a, b), add(b, a); // 无向图,双向建边
}
while (Q--) {
int u, dist;
cin >> u >> dist;
cout << (bfs(u, dist) ? "Yes" : "No") << endl;
}
return 0;
}
```
## 算法
(最短路,$BFS$) $O(n+m+q)$
本题关键点:
> 如果存在一条长度是 $L$ 的路径,其中 $L>0$,那么我们可以在其中任意一条边上来回走,就可以构造出来长度是 $L+2,L+4,L+6,…$的路径。
因此当我们想判断是否存在长度是 $L$ 的路径时,只需判断是否 **存在长度小于等于 $L$**,且 **奇偶性** 和 $L$ 相同的路径即可。
因此我们可以预处理出从$1$号点出发,到每个点长度为奇数的最短路径和长度为偶数的最短路径。
这里可以使用拆点技巧来构造新图,类似于$DP$中的[状态机模型](https://www.acwing.com/problem/content/1051/):
* 将原图中的每个点 $v$ 拆成两个新点:偶点$v_0$和奇点$v_1$;
* 将原图中的每条边 $(u,v)$ 拆成两条新边:$(u_0,v_1)$ 和 $(u_1,v_0)$;
那么在新图中从 $1$ 号点走到 $v_0$ 的所有路径,对应在原图中从 $1$ 号点走到 $v$ 的所有 **长度是偶数** 的路径;在新图中从 $1$ 号点走到 $v_1$ 的所有路径,对应在原图中从 $1$ 号点走到 $v$ 的所有 **长度是奇数** 的路径。
因此在新图上求出$1$号点到其他所有点的最短路径,即可求出在原图中从$1$号点到其他所有点的长度是奇数和偶数的最短路径。
由于所有边的长度为$1$,因此可以用$BFS$求最短路。
以上我们处理了 $L_i>0$ 的情况,还需特判一下 $L_i==0$ 的情况,$L_i==0$ 表示一条边都不存在,即$1$号点与其他点均不连通,此时由于输入时 $L_i≥1$,因此直接输出 $No$即可。
#### 时间复杂度
使用$BFS$求最短路的时间复杂度是 $(n+m)$;
判断每个查询操作的时间复杂度是 $O(1)$;
因此总时间复杂度是 $O(n+m+q)$。
```cpp {.line-numbers}
#include
using namespace std;
typedef pair PII;
#define x first // 节点号
#define y second // 奇偶性
const int N = 100010, M = 200010;
int n, m, Q;
int h[N], e[M], ne[M], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dist[N][2]; // 奇偶最短路
queue q;
// 因边边权都是1,不需要Dijkstra或者Floyd,只需要bfs即可
// 由于本题是强调 奇偶性 ,所以,需要使用 拆点 的思想
// 所谓拆点,就是像状态机或者DP中扩展维度的思想,将奇偶点分开,把混沌的事情清晰化。
// dist[i][0]:表示是偶数步的点,值是最小步数
// dist[i][1]:表示是奇数步的点
void bfs() {
memset(dist, 0x3f, sizeof dist); // 预求最短,先设最大
dist[1][0] = 0; // 1是起点,走0步到达即偶点,步数:0
q.push({1, 0}); // 起点入队列
while (q.size()) {
auto u = q.front();
q.pop();
for (int i = h[u.x]; ~i; i = ne[i]) { // u点
PII v = {e[i], u.y ^ 1};
// u.y ^ 1 奇<->偶 互换
// 由于上面的 y=u.y ^ 1,使得(u.x,u.y)只向(x,u.y的奇偶变换后数) 转移
// 这样做,就起到的拆点作用,而并不是真正的把点拆开
if (dist[v.x][v.y] > dist[u.x][u.y] + 1) { // 如果利用u可以更新v这个点
dist[v.x][v.y] = dist[u.x][u.y] + 1; // 更新
q.push(v); // v的最短距离更新了,入队列,去更新更多的点
}
}
}
}
int main() {
cin >> n >> m >> Q;
memset(h, -1, sizeof h);
while (m--) {
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
bfs();
while (Q--) {
int a, l;
cin >> a >> l;
/*
如果不写下面的特判,会被欺负死:
3 1 1
2 3
1 2
第一行三个正整数 n,m 和 q,分别表示工人的数目、传送带的数目和工单的数目。
也就是3个工人,1个传送带,1个工单
传送带是2~3,也就是1是与世隔绝的
接下来 q 行,每行两个正整数 a 和 L,表示编号为 a 的工人想生产一个第 L 阶段的零件。
1号工人,想生产2阶段的零件
由于1号工人是与世隔绝的,没有人给它提供1阶段的零件,肯定返回No,此时需要特判,返回答案
*/
if (h[1] == -1)
puts("No");
else if (l >= dist[a][l & 1]) // l是奇数,并且大于奇数最短路,则可以通过+2,+4,+6...等方法来回磨,凑够l就完事
// l是偶数,并且大于偶数最短路,则可以通过+2,+4,+6...等方法来回磨,凑够l就完事
puts("Yes");
else
puts("No");
}
return 0;
}
```
设求第$3$点为第$3$阶段时,点$1$是否需要提供原材料。
$【3,3】 => 【2,2】,【4,2】$
$【2,2】 => 【1,1】,【3,1】$
$【4,2】 => 【3,1】,【5,1】$
$【1,1】 => 【2,0】,【5,0】$
$【3,1】 => 【2,0】,【4,0】$
$【5,1】 => 【1,0】,【4,0】$ # 此处$1$需要提供原材料
比较容易想到对于每个询问进行暴搜,若点$1$为$0$,则$Yes$
时间复杂度很高,必然超时。
```cpp {.line-numbers}
#include
using namespace std;
typedef pair PII;
#define x first
#define y second
const int N = 1e5 + 10, M = N << 1;
// 20个测试点,过了7个,得了35分,其它TLE
// 邻接表
int e[M], h[N], idx, ne[M];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool bfs(int start, int dist) {
queue q;
q.push({start, dist});
while (q.size()) {
auto u = q.front();
q.pop();
if (u.x == 1 && u.y == 0) return true; // 在用完所有步数后,到达1号点,成功!
for (int i = h[u.x]; ~i; i = ne[i]) {
int v = e[i];
if (u.y) q.push({v, u.y - 1});
}
}
return false;
}
int main() {
memset(h, -1, sizeof h);
int n, m, Q;
cin >> n >> m >> Q;
while (m--) {
int a, b;
cin >> a >> b;
add(a, b), add(b, a); // 无向图,双向建边
}
while (Q--) {
int u, dist;
cin >> u >> dist;
cout << (bfs(u, dist) ? "Yes" : "No") << endl;
}
return 0;
}
```
## 算法
(最短路,$BFS$) $O(n+m+q)$
本题关键点:
> 如果存在一条长度是 $L$ 的路径,其中 $L>0$,那么我们可以在其中任意一条边上来回走,就可以构造出来长度是 $L+2,L+4,L+6,…$的路径。
因此当我们想判断是否存在长度是 $L$ 的路径时,只需判断是否 **存在长度小于等于 $L$**,且 **奇偶性** 和 $L$ 相同的路径即可。
因此我们可以预处理出从$1$号点出发,到每个点长度为奇数的最短路径和长度为偶数的最短路径。
这里可以使用拆点技巧来构造新图,类似于$DP$中的[状态机模型](https://www.acwing.com/problem/content/1051/):
* 将原图中的每个点 $v$ 拆成两个新点:偶点$v_0$和奇点$v_1$;
* 将原图中的每条边 $(u,v)$ 拆成两条新边:$(u_0,v_1)$ 和 $(u_1,v_0)$;
那么在新图中从 $1$ 号点走到 $v_0$ 的所有路径,对应在原图中从 $1$ 号点走到 $v$ 的所有 **长度是偶数** 的路径;在新图中从 $1$ 号点走到 $v_1$ 的所有路径,对应在原图中从 $1$ 号点走到 $v$ 的所有 **长度是奇数** 的路径。
因此在新图上求出$1$号点到其他所有点的最短路径,即可求出在原图中从$1$号点到其他所有点的长度是奇数和偶数的最短路径。
由于所有边的长度为$1$,因此可以用$BFS$求最短路。
以上我们处理了 $L_i>0$ 的情况,还需特判一下 $L_i==0$ 的情况,$L_i==0$ 表示一条边都不存在,即$1$号点与其他点均不连通,此时由于输入时 $L_i≥1$,因此直接输出 $No$即可。
#### 时间复杂度
使用$BFS$求最短路的时间复杂度是 $(n+m)$;
判断每个查询操作的时间复杂度是 $O(1)$;
因此总时间复杂度是 $O(n+m+q)$。
```cpp {.line-numbers}
#include
using namespace std;
typedef pair PII;
#define x first // 节点号
#define y second // 奇偶性
const int N = 100010, M = 200010;
int n, m, Q;
int h[N], e[M], ne[M], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dist[N][2]; // 奇偶最短路
queue q;
// 因边边权都是1,不需要Dijkstra或者Floyd,只需要bfs即可
// 由于本题是强调 奇偶性 ,所以,需要使用 拆点 的思想
// 所谓拆点,就是像状态机或者DP中扩展维度的思想,将奇偶点分开,把混沌的事情清晰化。
// dist[i][0]:表示是偶数步的点,值是最小步数
// dist[i][1]:表示是奇数步的点
void bfs() {
memset(dist, 0x3f, sizeof dist); // 预求最短,先设最大
dist[1][0] = 0; // 1是起点,走0步到达即偶点,步数:0
q.push({1, 0}); // 起点入队列
while (q.size()) {
auto u = q.front();
q.pop();
for (int i = h[u.x]; ~i; i = ne[i]) { // u点
PII v = {e[i], u.y ^ 1};
// u.y ^ 1 奇<->偶 互换
// 由于上面的 y=u.y ^ 1,使得(u.x,u.y)只向(x,u.y的奇偶变换后数) 转移
// 这样做,就起到的拆点作用,而并不是真正的把点拆开
if (dist[v.x][v.y] > dist[u.x][u.y] + 1) { // 如果利用u可以更新v这个点
dist[v.x][v.y] = dist[u.x][u.y] + 1; // 更新
q.push(v); // v的最短距离更新了,入队列,去更新更多的点
}
}
}
}
int main() {
cin >> n >> m >> Q;
memset(h, -1, sizeof h);
while (m--) {
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
bfs();
while (Q--) {
int a, l;
cin >> a >> l;
/*
如果不写下面的特判,会被欺负死:
3 1 1
2 3
1 2
第一行三个正整数 n,m 和 q,分别表示工人的数目、传送带的数目和工单的数目。
也就是3个工人,1个传送带,1个工单
传送带是2~3,也就是1是与世隔绝的
接下来 q 行,每行两个正整数 a 和 L,表示编号为 a 的工人想生产一个第 L 阶段的零件。
1号工人,想生产2阶段的零件
由于1号工人是与世隔绝的,没有人给它提供1阶段的零件,肯定返回No,此时需要特判,返回答案
*/
if (h[1] == -1)
puts("No");
else if (l >= dist[a][l & 1]) // l是奇数,并且大于奇数最短路,则可以通过+2,+4,+6...等方法来回磨,凑够l就完事
// l是偶数,并且大于偶数最短路,则可以通过+2,+4,+6...等方法来回磨,凑够l就完事
puts("Yes");
else
puts("No");
}
return 0;
}
```
