##[$AcWing$ $456$ 车站分级](https://www.acwing.com/problem/content/458/)

### 一、题目描述
一条 **单向** 的铁路线上，依次有编号为 $1, 2, …, n$ 的 $n$ 个火车站。

每个火车站都有一个级别，最低为 $1$ 级。

现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 $x$，则始发站、终点站之间所有级别 **大于等于** 火车站 $x$ 的都必须停靠。（**注意：起始站和终点站自然也算作事先已知需要停靠的站点**） 

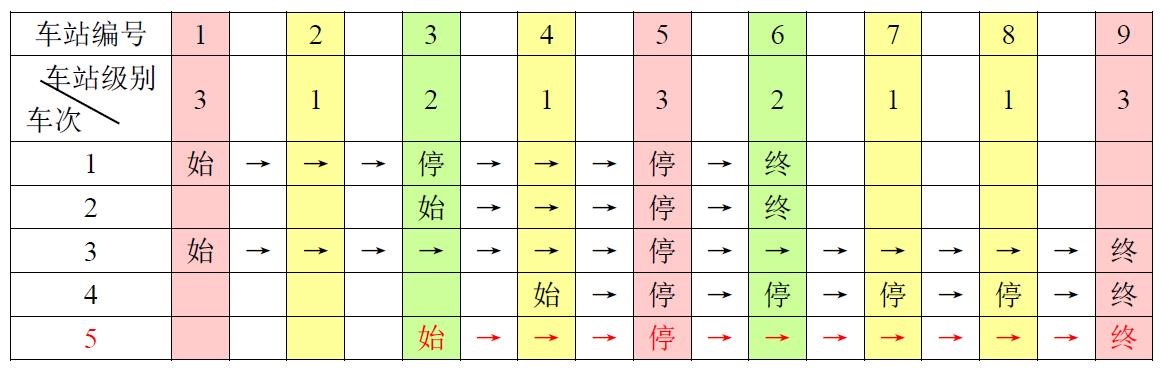
例如，下表是 $5$ 趟车次的运行情况。

其中，前 $4$ 趟车次均满足要求，而第 $5$ 趟车次由于停靠了 $3$ 号火车站（$2$ 级）却未停靠途经的 $6$ 号火车站（亦为 $2$ 级）而不满足要求。

<center><img src='https://www.acwing.com/media/article/image/2019/03/11/19_8d0e0df443-1163900-20170818013814084-1540659827.jpg'></center>

现有 $m$ 趟车次的运行情况（**全部满足要求**），试推算这 $n$ 个火车站 **至少** 分为几个不同的级别。

**输入格式**
第一行包含 $2$ 个正整数 $n,m$，用一个空格隔开。

第 $i+1$ 行（$1≤i≤m$）中，首先是一个正整数 $s_i（2≤s_i≤n）$，表示第 $i$ 趟车次有 $s_i$ 个停靠站；接下来有 $s_i$ 个正整数，表示所有停靠站的编号，从小到大排列。

每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

**输出格式**
输出只有一行，包含一个正整数，即 $n$ 个火车站最少划分的级别数。

**数据范围**
$1≤n,m≤1000$

**输入样例**：
```cpp {.line-numbers}
9 3 
4 1 3 5 6 
3 3 5 6 
3 1 5 9 
```

**输出样例**：
```cpp {.line-numbers}
3
```


### 二、算法

**差分约束** 裸题。

计算 **当前线路中最小的级别**（包括始发站和终点站）。
整条线路中所有 **大于等于** 这个级别的都 **必须停靠**, **所有未停靠的站点的级别一定小于这个级别**。

也就是说所有 <font color='red' size=4><b>未停靠的站点</b></font> 即为级别低,记为$A$,所有 <font color='red' size=4><b>停靠的站点</b></font> 级别一定比$A$的高，记作$B$。

得到公式
$$\large B≥A+1$$

很明显是一道 **差分约束** 的问题。

根据差分约束的概念，我们从所有的$A$向所有的$B$连一条权值为$1$的有向边,描述$B>=A+1$。

然后根据差分约束的 **套路**，我们 **还要设一个界限才能求出最大值**。

因为所有车站级别都是正值，所以$A≥1$，也就是从$0$向所有的$A$中的点连一条权值为$1$ 的有向边。

但是由于实际数据范围较大，最坏情况下是有$1000$趟火车，每趟有$1000$个点，<font color='red' size=4><b>由于我们是用未停靠站向需停靠站连边，想要计算边数量的最大值是多少，</b></font>每趟上限有$500$个点停站，则有$(1000 - 500)$个点不停站，不停站的站点都向停站的站点连有向边，则总共有 $500∗500∗1000=2.5∗10^8$，差分约束的$spfa$有可能超时。
> **解释**：为啥是$500$呢？因为共$1000$个点，$a+b=1000$,预使$a*b$最大，当然是$a=b=500$时。
> 

#### 拓扑排序优化

由于本题中的所有点的权值都是大于$0$，并且一定满足要求=>所有车站都等级森严=>不存在环=>可以 **拓扑排序得到拓扑图使用递推求解差分约束问题**。


**整体思路**
- ① 拓扑排序得拓扑图
- ② **至少** =>要求的是 **最小值**=>所有条件的下界中取最大值=>**最长路**，因此我们，根据 **拓扑序跑最长路递推即可**。
- ③ 答案为满足所有约束条件的解中最大值既是题目要求的最高的级别

**建图优化**

如果直接暴力建图就会建$O(nm)$ 条边，也就是$2∗10^8$个点，时间和空间都有可能超时。

我们可以在中间建一个虚拟节点，左边向虚拟点连$0$，虚拟点向右边连$1$等价于左边向右边连$1$。

这样只会建$O(n+m)$条边

注意的是本题一共$m$条线路,每条线路一个虚拟源点,所以一共会有$n + m$个点。


可以在中间建一个虚拟节点，左边向虚拟点连$0$，虚拟点向右边连$1$等价于左边向右边连$1$。

这样只会建$O(n+m)$条边


优化前：

<center><img src='https://img-blog.csdnimg.cn/20200731170038971.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NTY5Nzc3NA==,size_16,color_FFFFFF,t_70'></center>

<center><img src='https://img-blog.csdnimg.cn/202007311701072.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80NTY5Nzc3NA==,size_16,color_FFFFFF,t_70'></center>

### 三、记忆化搜索
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int N = 2010, M = 1000010;
int n, m;
int d[N];
int st[N];

int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int dfs(int u) {
    if (~d[u]) return d[u]; // 记忆化搜索
    d[u] = 1;               // 最少是一级
    for (int i = h[u]; ~i; i = ne[i]) {
        int j = e[i];
        d[u] = max(d[u], dfs(j) + w[i]);
    }
    return d[u];
}

int main() {
#ifndef ONLINE_JUDGE
    freopen("456.in", "r", stdin);
#endif

    ios::sync_with_stdio(false), cin.tie(0);
    cin >> n >> m;

    memset(h, -1, sizeof h);
    for (int i = 1; i <= m; i++) {
        memset(st, 0, sizeof st);

        int k;
        cin >> k;
        int S = n, T = 1;
        for (int j = 1; j <= k; j++) {
            int x;
            cin >> x;
            S = min(S, x);
            T = max(T, x);
            st[x] = 1;
        }

        for (int j = S; j <= T; j++)
            if (st[j])
                add(n + i, j, 1);
            else
                add(j, n + i, 0);
    }

    int res = 0;
    memset(d, -1, sizeof d);
    for (int i = 1; i <= n; i++) res = max(res, dfs(i));
    printf("%d\n", res);
    return 0;
}
```


### 四、优化建图+拓扑序+递推求解最长路
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int N = 2010, M = 1000010;
const int INF = 0x3f3f3f3f;
int n, m;
int in[N];
int dist[N];
int st[N];

// 邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
vector<int> path; // 拓扑路径
void topsort() {
    queue<int> q;
    /*
    考虑极限情况：当每一个站点全部停靠的情况下，相当于左侧集合为空（不停靠的没有）
    也就没有左侧集合向虚拟点连边这件事，虚拟点的入度为0,此时，虚拟点需要入队列
    */
    for (int i = 1; i <= n + m; i++)
        if (!in[i]) q.push(i);

    while (q.size()) {
        int u = q.front();
        q.pop();
        path.push_back(u);
        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            in[j]--;
            if (in[j] == 0) q.push(j);
        }
    }
}

int main() {
    // 加快读入
    ios::sync_with_stdio(false), cin.tie(0);
    // 建图
    memset(h, -1, sizeof h);
    cin >> n >> m; // n个火车站,m趟车次

    for (int i = 1; i <= m; i++) {
        memset(st, 0, sizeof st); // 记录哪些是停靠点

        int k;
        cin >> k; // 有多少个依靠站
        int S = n, T = 1;
        for (int j = 1; j <= k; j++) {
            int x; // 停靠站编号
            cin >> x;
            S = min(S, x); // 第一个停靠点
            T = max(T, x); // 最后一个停靠点
            st[x] = 1;     // 记录哪些是停靠点，哪些不是停靠点
        }
        // 笛卡尔积式建图优化技巧
        int u = n + i; // 分配超级源点，虚拟点点号。多条线路，每次一个超级源点，共多建超级源点m个
        for (int j = S; j <= T; j++)
            if (st[j])                 // 如果j不是停靠点
                add(u, j, 1), in[j]++; // 虚拟点向右侧集合中每个点连一条长度为1的边
            else
                add(j, u, 0), in[u]++; // 左侧集合向 虚拟点u 连一条长度为0的边
    }

    // 求拓扑序
    topsort();

    /*
    Q:for (int i = 1; i <= n; i) dist[i] = 1;
    y总这句话为什么不能这样写呀 for (int i = 1; i <= n + m; i) dist[i] = 1;

    A:考虑一种边界情况，当全部站点都停靠的时候,此时虚拟节点是入度为0的节点，虚拟节点的等级dist应该为0，
    因为连向车站的边权已经是1,否则，如果虚拟节点的等级为1，那么连向的车站等级就会是2。
    */

    // 递推距离初始化
    for (int i = 1; i <= n; i++) dist[i] = 1; // n个站点的等级最少是1，而虚拟节点的等级最少是0
    // 拓扑路径+递推计算最长路
    for (auto u : path) // 枚举拓扑路径的每一个点
        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            dist[j] = max(dist[j], dist[u] + w[i]); // u要求j必须距离自己>=w[i]
        }

    int res = 0;
    for (int i = 1; i <= n; i++) res = max(res, dist[i]); // 找出最大值，就是最小等级
    printf("%d\n", res);
    return 0;
}
```