## [$AcWing$ $419$. $FBI$树](https://www.acwing.com/problem/content/description/421/)

### 一、题目描述
我们可以把由 $0$ 和 $1$ 组成的字符串分为三类：全 $0$ 串称为 $B$ 串，全 $1$ 串称为 $I$ 串，既含 $0$ 又含 $1$ 的串则称为 $F$ 串。

$FBI$ 树是一种二叉树，它的结点类型也包括 $F$ 结点，$B$ 结点和 $I$ 结点三种。

由一个长度为 $2^N$ 的 $01$ 串 $S$ 可以构造出一棵 $FBI$ 树 $T$，递归的构造方法如下：

$T$ 的根结点为 $R$，其类型与串 $S$ 的类型相同；
若串 $S$ 的长度大于 $1$，将串 $S$ 从中间分开，分为等长的左右子串 $S_1$ 和 $S_2$
；由左子串 $S_1$ 构造 $R$ 的左子树 $T_1$，由右子串 $S_2$ 构造 $R$ 的右子树 $T_2$。
现在给定一个长度为 $2^N$ 的 $01$ 串，请用上述构造方法构造出一棵 $FBI$ 树，并输出它的后序遍历序列。

**输入格式**
第一行是一个整数 $N$。

第二行是一个长度为 $2^N$ 的 $01$ 串。

**输出格式**
包含一行，这一行只包含一个字符串，即 $FBI$ 树的后序遍历序列。

**数据范围**
$0≤N≤10$

**输入样例**：
```cpp {.line-numbers}
3
10001011
```

**输出样例**：
```cpp {.line-numbers}
IBFBBBFIBFIIIFF
```

### 二、算法

(递归,二叉树) $O((N+1)2^N)$ 
对于样例来说，我们可以得到如下所示的满二叉树：

![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/{year}/{month}/{md5}.{extName}/202310111052999.png)

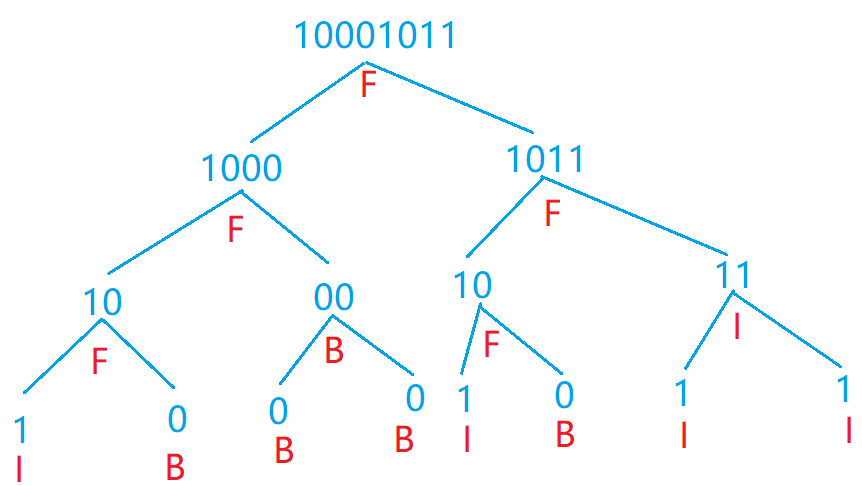
可以递归处理整棵树，我们发现当输入字符串固定时，整棵树也就固定了，因此可以将字符串当做递归函数传入的参数。

由于要输出后序遍历，因此需要先输出左子树和右子树，再输出当前节点的信息。

从图中可以发现，左子树所对应的字符串即是当前字符串的前半段，右子树所对应的字符串是后半段。因此依次递归处理字符串的前半段和后半段即可。

最后需要判断当前节点的类型，这里可以统计一下当前字符串中$0$和$1$的包含情况。

**时间复杂度**
在每个递归函数内判断当前节点的类型时，均需要遍历一遍整个字符串，因此时间复杂度是线性的。从上图中可以发现，整棵树一共有 $N+1$ 层，每层总共会遍历 $O(N)$ 的长度，因此总时间复杂度是 $O(N+1)2^N$。

><font color='red' size=4><b>注:因为要判断每个字符串中$0$和$1$的个数，需要扫描一遍全部字符，就是整体上看是$2^N$,有$N+1$层</b></font>

### 三、实现代码
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;

void dfs(string str) {
    if (str.size() > 1) {
        dfs(str.substr(0, str.size() / 2)); // 左子树
        dfs(str.substr(str.size() / 2));    // 右子树
    }
    // 我该输出啥？
    int one = 0, zero = 0;
    for (int i = 0; i < str.size(); i++)
        if (str[i] == '0')
            zero++;
        else
            one++;

    if (one && zero)
        cout << 'F';
    else if (one)
        cout << 'I';
    else
        cout << 'B';
}

int main() {
    int n;
    string str;
    cin >> n >> str;

    dfs(str);
    return 0;
}

```