##[$AcWing$ $1319$. 移棋子游戏](https://www.acwing.com/problem/content/description/1321/)

### 一、题目描述
给定一个有 $N$ 个节点的 **有向无环图**，图中某些节点上有棋子，两名玩家交替移动棋子。

玩家每一步可将任意一颗棋子沿一条有向边移动到另一个点，无法移动者输掉游戏。

对于给定的图和棋子初始位置，双方都会采取最优的行动，询问先手必胜还是先手必败。

**输入格式**
第一行，三个整数 $N,M,K$，$N$ 表示图中节点总数，$M$ 表示图中边的条数，$K$ 表示棋子的个数。

接下来 $M$ 行，每行两个整数 $X,Y$ 表示有一条边从点 $X$ 出发指向点 $Y$。

接下来一行， $K$ 个空格间隔的整数，表示初始时，棋子所在的节点编号。

节点编号从 $1$ 到 $N$。

**输出格式**
若先手胜，输出 `win`，否则输出 `lose`。

**数据范围**
$1≤N≤2000,1≤M≤6000,1≤K≤N$

**输入样例：**
```cpp {.line-numbers}
6 8 4
2 1
2 4
1 4
1 5
4 5
1 3
3 5
3 6
1 2 4 6
```

**输出样例：**
```cpp {.line-numbers}
win
```

### 二、解题思路

#### 1、$SG$函数
首先定义 $mex$ 函数，这是施加于一个集合的函数，返回　**最小的不属于这个集合的非负整数**

例：$mex({1,2})=0,mex({0,1})=2,mex({0,1,2,4})=3$

在一张有向无环图中，对于每个点 $u$，设其 **所有能到的点** 的 $SG$ 函数值集合为集合 $A$，那么 $u$ 的 $SG$ 函数值为 $mex(A)$，记做 $SG(u)=mex(A)$

如图：
<center><img src='https://cdn.acwing.com/media/article/image/2020/06/25/30334_2388c086b6-%E6%97%A0%E6%A0%87%E9%A2%98.png'></center>

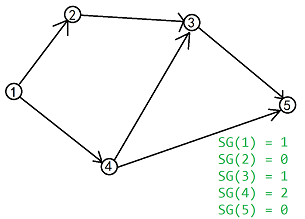**例图解释**：

$SG(5)=mex({\phi})=0$
$SG(3)=mex({SG(5)})=mex({0})=1$
$SG(4)=mex({SG(5),SG(3)})=mex({0,1})=2$
$SG(2)=mex({SG(3)})=mex({1})=0$
$SG(1)=mex({SG(2),SG(4)})=mex({0,2})=1$

#### 2、本题和 $SG$ 函数有什么关系？
下面先说本题做法，再证明该方法正确性。

**做法**：求出每个棋子所在的点的 $SG$ 函数值，将所有值异或起来。若异或值不为 $0$，则输出$win$，否则输出$lose$

**证明**：
首先，由于这是一张有向无环图，所以游戏最后一定会结束，也就是说每个棋子最后都会移动到一个点上，且该点没有任何能到达的点。

根据定义，结束状态的所有点的 $SG$ 函数值异或起来为 $0$，**做法对于结束状态可行**。

所以接下来，只要证明出

- ① 任何一种每个棋子所在点的 $SG$ 函数值异或起来非 $0$ 的情况，一定能通过一次移动棋子，到达一个 每个棋子所在点的 $SG$ 函数值异或起来为 $0$ 的情况

- ② 任何一种每个棋子所在点的 $SG$ 函数值异或起来为 $0$ 的情况，一定不能通过一次移动棋子，到达一个每个棋子所在点的 $SG$  函数值异或起来为 $0$ 的情况

那么做法就是对的


**证明** $1$：
设每个棋子所在点的 $SG$ 函数值分别为 $a_1,a_2,⋯,a_n$
设 $x=a_1 XOR a_2 XOR ⋯ XOR a_n$，**此时$x$一定不等于$0$**。
设 $x$ 的最高位为第 $k$ 位，那么在 $a_1,a_2,⋯,a_n$ 中，一定有一个值的第 $k$ 位为 $1$。
设该值为 $a_i$，那么由于 $x$ 的第 $k$位和 $a_i$ 的第 $k$ 位都是 $1$,且,第 $k$ 位是 $x$ 的最高位，所以 $a_i XOR x$ 一定小于 $a_i$

又因为 $a_i$ 是其中一个棋子所在点的 $SG$ 函数值，那么根据 $SG$ 函数值的定义，该点能到达的所有点中，一定存在一个点的 $SG$ 函数值为 $a_i XOR x$

那么我们就可以将该点上的棋子，移到一个 $SG$ 函数值为 $a_i XOR x$ 的点上去

**移完之后**，原来每个棋子所在点的 $SG$ 函数异或值就变为了 $a_1 XOR a_2 XOR ⋯ XOR a_{i−1} XOR (a_i XOR x) XOR a_{i+1} ⋯ XOR a_n$

$=(a_1 XOR a_2 XOR ⋯ XOR a_n) XOR x=x XOR x=0$

① 证毕


**证明** $2$：
反证法，设将点 $u$ 上的棋子移动到点 $v$ 上后，每个棋子所在点的 $SG$ 函数值仍然为 $0$
那就说明 $SG(u)=SG(v)$，不符合 $SG$ 函数的定义，不成立
② 证毕

所以做法是正确的。

#### 3、如何求出每个点的 $SG$ 函数值呢？
记忆化搜索就好啦~
每层记忆化搜索中，如果该点的 $SG$ 函数值已经被计算出，那就直接返回该值。否则用一个 $set$ 记录每个点能到的所有点的 $SG$ 函数值集合，然后从 $0$ 开始遍历，找到第一个 $set$ 里面没有的数，将该值记录在该点上并返回。


### 三、实现代码
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int N = 2010, M = 6010;

// SG函数模板题
int n, m, k;
int f[N];

int h[N], e[M], ne[M], idx;
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int sg(int u) {
    //记忆化搜索
    if (~f[u]) return f[u];

    //找出当前结点u的所有出边，看看哪个sg值没有使用过
    set<int> S;
    for (int i = h[u]; ~i; i = ne[i])
        S.insert(sg(e[i]));

    //找到第一个没有出现的过的自然数， 0,1,2,3,4,...
    for (int i = 0;; i++)
        if (S.count(i) == 0) {
            f[u] = i;
            break;
        }
    return f[u];
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m >> k;
    while (m--) {
        int a, b;
        cin >> a >> b;
        add(a, b);
    }

    memset(f, -1, sizeof f); //初始化sg函数的结果表
    int res = 0;
    while (k--) {
        int u;
        cin >> u;
        res ^= sg(u); //计算每个出发点的sg(u)，然后异或在一起
    }

    if (res) //所有出发点的异或和不等于0,先手必胜
        puts("win");
    else //所有出发点的异或和等于0，先手必败
        puts("lose");

    return 0;
}
```