## [$AcWing$ $1131$ 拯救大兵瑞恩](https://www.acwing.com/problem/content/1133/)

### 一、题目描述
$1944$年，特种兵麦克接到国防部的命令，要求立即赶赴太平洋上的一个孤岛，营救被敌军俘虏的大兵瑞恩。

瑞恩被关押在一个迷宫里，迷宫地形复杂，但幸好麦克得到了迷宫的地形图。

迷宫的外形是一个长方形，其南北方向被划分为 $N$ 行，东西方向被划分为 $M$ 列， 于是整个迷宫被划分为 $N×M$ 个单元。

每一个单元的位置可用一个有序数对 (单元的行号, 单元的列号) 来表示。

南北或东西方向相邻的 $2$ 个单元之间 **可能互通**，**也可能有一扇锁着的门**，或者是**一堵不可逾越的墙**。

注意： 门可以从两个方向穿过，即可以看成一条 **无向边**。

迷宫中有一些单元存放着 **钥匙** ，同一个单元可能存放 **多把钥匙**，并且所有的门被分成 $P$ 类，**打开同一类的门的钥匙相同，不同类门的钥匙不同**。

大兵瑞恩被关押在迷宫的东南角，即 $(N,M)$ 单元里，并已经昏迷。

迷宫只有一个入口，在**西北角**。

也就是说，麦克可以直接进入 $(1,1)$ 单元。

另外，麦克从一个单元移动到另一个相邻单元的时间为 $1$，拿取所在单元的钥匙的时间以及用钥匙开门的时间可忽略不计。

试设计一个算法，帮助麦克以 **最快** 的方式到达瑞恩所在单元，营救大兵瑞恩。

**输入格式**
第一行有三个整数,分别表示 $N,M,P$ 的值。

第二行是一个整数 $k$，表示迷宫中门和墙的总数。

接下来 $k$ 行，每行包含五个整数，$X_{i1},Y_{i1},X_{i2},Y_{i2},G_i$：当 $G_i≥1$ 时，表示 $(X_{i1},Y_{i1})$ 单元与 ($X_{i2},Y_{i2}$) 单元之间有一扇第 $G_i$ 类的门，当 $G_i=0$ 时，表示 $(X_{i1},Y_{i1})$ 单元与 ($X_{i2},Y_{i2}$) 单元之间有一面不可逾越的 **墙**。

接下来一行，包含一个整数 $S$，表示迷宫中存放的 **钥匙的总数**。

接下来 $S$ 行，每行包含三个整数 $X_{i1},Y_{i1},Q_i$，表示 ($X_{i1},Y_{i1}$) 单元里存在一个能开启第 $Q_i$ 类门的钥匙。

**输出格式**
输出麦克营救到大兵瑞恩的最短时间。

如果问题无解，则输出 $-1$。

**数据范围**
$|X_{i1}−X_{i2}|+|Y_{i1}−Y_{i2}|=1$
$0≤G_i≤P$
$1≤Q_i≤P$
$1≤N,M,P≤10$
$1≤k≤150$

**输入样例**：
```cpp {.line-numbers}
4 4 9
9
1 2 1 3 2
1 2 2 2 0
2 1 2 2 0
2 1 3 1 0 
2 3 3 3 0
2 4 3 4 1
3 2 3 3 0
3 3 4 3 0
4 3 4 4 0
2
2 1 2 
4 2 1
```

**输出样例**：
```cpp {.line-numbers}
14
```

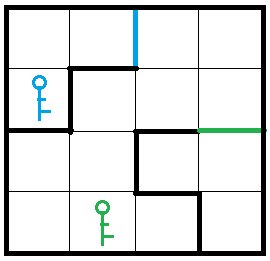
**样例解释**：
迷宫如下所示：
![](https://cdn.acwing.com/media/article/image/2019/11/06/1_17c87ee400-1131.png)


### 二、解题思路
试想下如果本题 **没有钥匙和门** 的条件，只要求从 **左上角** 走到 **右下角** 的最小步数，就是简单的迷宫问题了，可以使用$bfs$解决。

#### 状态表示
加上钥匙和门的的条件，便是**类似于八数码问题**了。实际上$bfs$解决的最短路问题都可以看作 **求从初始状态到结束状态需要的最小转移次数**:

普通迷宫问题的 **状态** 就是 **当前所在的坐标**，八数码问题的 **状态** 就是 **当前棋盘的局面**。

本题在迷宫问题上加上了 **钥匙和门** 的条件，显然，处在同一个坐标下，**持有钥匙和不持有钥匙就不是同一个状态了**，为了能够清楚的表示每个状态，除了当前坐标外还需要加上当前获得的钥匙信息，即$f[x][y][st]$表示当前处在$(x，y)$位置下持有钥匙状态为$st$，将二维坐标压缩成一维就得到$f[z][st]$这样的状态表示了，或者说，$z$是格子的编号，从上到下，从左而右的编号依次为$1$到$n*m$，$st$为$0110$时，表示持有第$1,2$类钥匙，这里注意我在 <font color='red'><b>表示状态时抛弃了最右边的一位</b></font>，因为钥匙编号从$1$开始，我想确定是否持有第$i$类钥匙时，只需要判断`st >> i & 1`是不是等于$1$即可。

知道了状态表示，现在题目就转化为了从状态$f[1][0]$转化为$f[n*m][…]$状态的 **最小步数**了，我们不关心到达终点是什么状态，**只要到达了终点就成功了**。

#### 状态转移
这里的记录方法就是用$PII$的记录每个格子，$g[PII][PII]$的值描述是否有墙；
* 两个相邻格子间有墙，就不能转移
* 有门，持有该类门钥匙就能转移，没有钥匙就不能转移
* 没有障碍，正常转移

下面讨论转移到有钥匙的格子的情况，我们走到有钥匙的格子上，并不用考虑要不要拿钥匙，拿钥匙又不会增加成本，只管拿就行。因此，转移到某个格子时，直接计算下这个格子的状态，格子上有钥匙就在之前状态基础上 **加上这个钥匙**，没有钥匙就继承之前的钥匙状态。

本题看起来复杂，实际上不过是动态规划、$bfs$和 **状态压缩** 三者的结合，还是比较 **简单** 的。

### 三、$bfs$解法
```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 105, M = 12;
typedef pair<int, int> PII;

int g[N][N];              // 两个位置之间的间隔是什么，可能是某种门，或者是墙
int key[N];               // 某个坐标位置上有哪些钥匙，这是用数位压缩记录的,方便位运算
int dis[N][1 << M];       // 哪个位置，在携带不同的钥匙情况下的状态
int n, m;                 // n行m列
int k;                    // 迷宫中门和墙的总数
int p;                    // p类钥匙
int dx[] = {-1, 0, 1, 0}; // 上右下左
int dy[] = {0, 1, 0, -1}; // 上右下左

// 二维转一维的办法,坐标从(1,1)开始
int get(int x, int y) {
    return (x - 1) * m + y;
}

int bfs() {
    memset(dis, 0x3f, sizeof dis); // 初始化距离
    queue<PII> q;                  // bfs用的队列

    int S = get(1, 1);   // 从编号1出发
    q.push({S, key[S]}); // 位置+携带钥匙的压缩状态 = 现在的真正状态
    dis[S][key[S]] = 0;  // 初始状态的需要走的步数为0

    while (q.size()) {
        PII x = q.front();
        q.pop();

        int u = x.first;   // 出发点编号
        int st = x.second; // 钥匙状态,为状态压缩的数字

        // dis[u][st]:到达了n*m,并且，当前状态是st: 找到大兵瑞恩就结束了,不用管最终的钥匙状态是什么
        // 是什么都是符合拯救大兵的目标的
        if (u == n * m) return dis[u][st];

        // 四个方向
        for (int i = 0; i < 4; i++) {
            // 注意这里我是将格子编号从1开始，因此将其转化为坐标时需要先减一再加一
            int tx = (u - 1) / m + 1 + dx[i]; // 下一个位置
            int ty = (u - 1) % m + 1 + dy[i];

            int T = get(tx, ty); // 要去的坐标位置T

            /*
            g[z][T] == 0 有墙，不能走
            g[z][T] >  0 有门，有钥匙能走，无钥匙不能走
            g[z][T] == -1 随便走
            */
            // 出界或有墙,没有办法转移
            if (tx == 0 || ty == 0 || tx > n || ty > m || g[u][T] == 0) continue;

            // 有门,并且, st这个状态中没有带过来当前类型的钥匙
            if (g[u][T] > 0 && !(st >> g[u][T] & 1)) continue;

            // 捡起钥匙不会增加成本，所以，无条件捡起来钥匙
            int ST = st | key[T];

            // 如果这个状态没有走过
            if (dis[T][ST] == INF) {
                q.push({T, ST});             // 入队列
                dis[T][ST] = dis[u][st] + 1; // 步数加1
            }
        }
    }
    // 一直没走到，返回-1
    return -1;
}
int main() {
    scanf("%d %d %d %d", &n, &m, &p, &k); // 地图n行m列，p类钥匙,k:迷宫中门和墙的总数

    // 地图初始化
    memset(g, -1, sizeof g);

    // 1、将图记下来
    int x1, y1, x2, y2, z1, z2, z;
    while (k--) { // 读入迷宫中门和墙
        // z=0:墙，z ={1,2,3,4...}哪种类型的门
        scanf("%d %d %d %d %d", &x1, &y1, &x2, &y2, &z);
        // 二维转化一维
        // Q:为什么一定要二维转一维呢？不转直接用二维不行吗？
        // A:点是一个二维信息，将坐标转换为点的编号，这样数组不用声明更多维度，代码更简单
        z1 = get(x1, y1), z2 = get(x2, y2);
        // 记录两个位置之间的间隔是:墙？某种类型的门？
        g[z1][z2] = g[z2][z1] = z; // 无向图
    }

    int s;
    scanf("%d", &s);
    while (s--) {                        // 枚举每把钥匙
        scanf("%d %d %d", &x1, &y1, &z); // 位置+钥匙类型
        // 利用状态压缩，描述此位置上有钥匙
        //  get(x1,y1)--->1维转换后的数字
        //  key[get(x1,y1)]利用二进制+位运算，记录此位置有哪些类型的钥匙,因为一个位置可以有多个类型的钥匙，所以采用 |运算符进行累加
        //   1 << z ：放过最后一位，将倒数第z位设置为数字1
        key[get(x1, y1)] |= 1 << z;
    }
    // 宽搜
    printf("%d\n", bfs());
    return 0;
}

```