## [$AcWing$ $787$. 归并排序](https://www.acwing.com/problem/content/description/789/)
### 一、题目描述
给定你一个长度为 $n$ 的整数数列。
请你使用 **归并排序** 对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
**输入格式**
输入共两行,第一行包含整数 $n$。
第二行包含 $n$ 个整数(所有整数均在 $1∼10^9$ 范围内),表示整个数列。
**输出格式**
输出共一行,包含 $n$ 个整数,表示排好序的数列。
**数据范围**
$1≤n≤100000$
**输入样例:**
```cpp {.line-numbers}
5
3 1 2 4 5
```
**输出样例:**
```cpp {.line-numbers}
1 2 3 4 5
```
### 二、算法原理
 ### 二、实例模拟
具体的我们以一组无序数列$\{14,12,15,13,11,16 \}$为例分解说明,如下图所示:
### 二、实例模拟
具体的我们以一组无序数列$\{14,12,15,13,11,16 \}$为例分解说明,如下图所示:
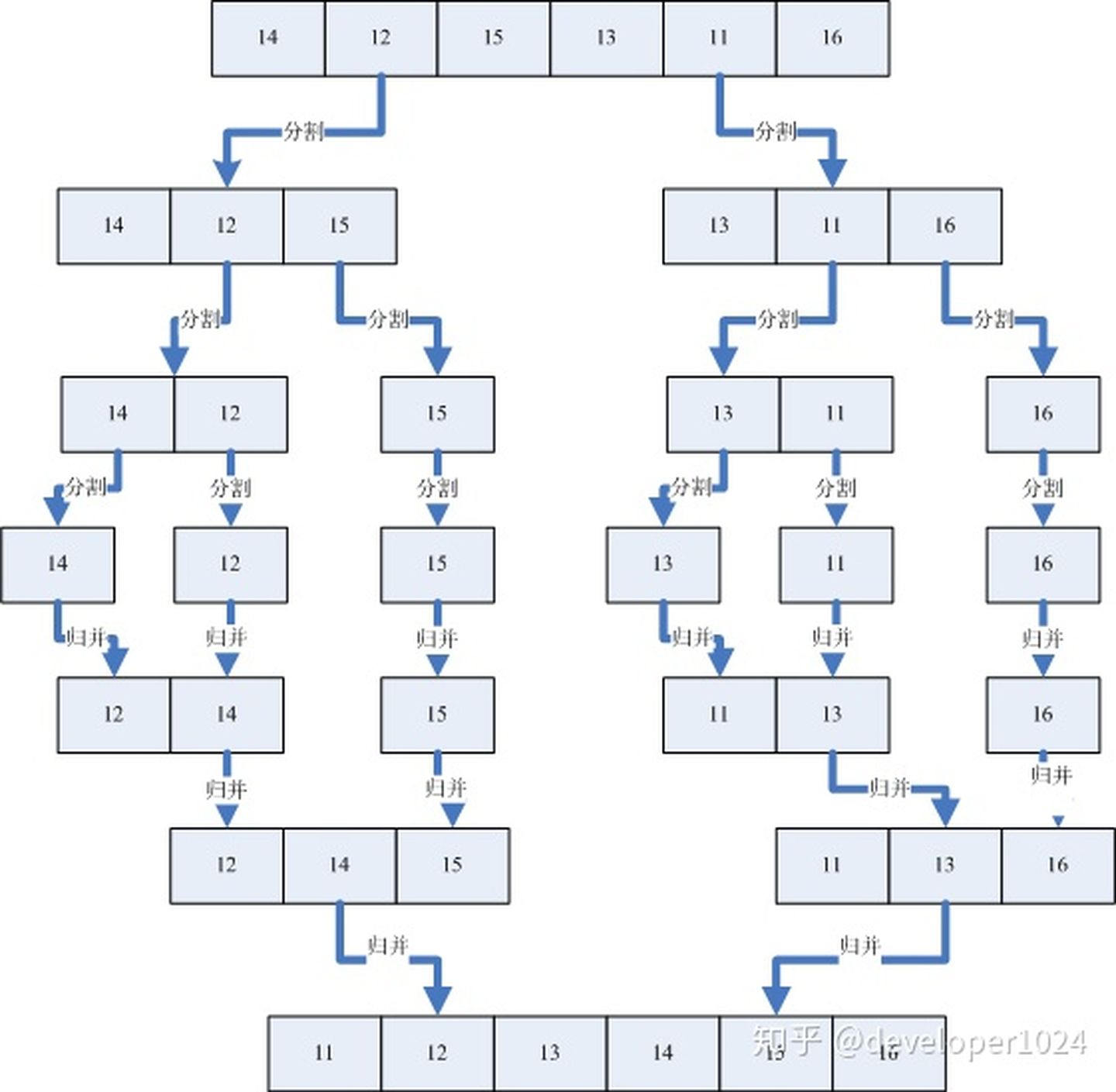 上图中首先把一个未排序的序列从中间分割成$2$部分,再把$2$部分分成$4$部分,依次分割下去,直到分割成一个一个的数据,再把这些数据两两归并到一起,使之有序,不停的归并,最后成为一个排好序的序列。
### 三、代码模板
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1e5 + 10;
int q[N], t[N];
void merge_sort(int q[], int l, int r) {
if (l >= r) return;
int mid = (l + r) >> 1;
merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r)
if (q[i] <= q[j])
t[k++] = q[i++];
else
t[k++] = q[j++];
while (i <= mid) t[k++] = q[i++];
while (j <= r) t[k++] = q[j++];
for (i = l, j = 0; i <= r; i++, j++) q[i] = t[j];
}
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) cin >> q[i];
merge_sort(q, 1, n);
for (int i = 1; i <= n; i++) printf("%d ", q[i]);
return 0;
}
```
上图中首先把一个未排序的序列从中间分割成$2$部分,再把$2$部分分成$4$部分,依次分割下去,直到分割成一个一个的数据,再把这些数据两两归并到一起,使之有序,不停的归并,最后成为一个排好序的序列。
### 三、代码模板
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1e5 + 10;
int q[N], t[N];
void merge_sort(int q[], int l, int r) {
if (l >= r) return;
int mid = (l + r) >> 1;
merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
int i = l, j = mid + 1, k = 0;
while (i <= mid && j <= r)
if (q[i] <= q[j])
t[k++] = q[i++];
else
t[k++] = q[j++];
while (i <= mid) t[k++] = q[i++];
while (j <= r) t[k++] = q[j++];
for (i = l, j = 0; i <= r; i++, j++) q[i] = t[j];
}
int main() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) cin >> q[i];
merge_sort(q, 1, n);
for (int i = 1; i <= n; i++) printf("%d ", q[i]);
return 0;
}
``` ### 二、实例模拟
具体的我们以一组无序数列$\{14,12,15,13,11,16 \}$为例分解说明,如下图所示:
### 二、实例模拟
具体的我们以一组无序数列$\{14,12,15,13,11,16 \}$为例分解说明,如下图所示:
 上图中首先把一个未排序的序列从中间分割成$2$部分,再把$2$部分分成$4$部分,依次分割下去,直到分割成一个一个的数据,再把这些数据两两归并到一起,使之有序,不停的归并,最后成为一个排好序的序列。
### 三、代码模板
```cpp {.line-numbers}
#include
上图中首先把一个未排序的序列从中间分割成$2$部分,再把$2$部分分成$4$部分,依次分割下去,直到分割成一个一个的数据,再把这些数据两两归并到一起,使之有序,不停的归并,最后成为一个排好序的序列。
### 三、代码模板
```cpp {.line-numbers}
#include