##[$AcWing$ $905$. 区间选点](https://www.acwing.com/problem/content/description/907/)
### 一、题目描述
给定 $N$ 个闭区间 $[a_i,b_i]$,请你在数轴上 **选择尽量少的点**,**使得每个区间内至少包含一个选出的点**。
输出选择的点的最小数量。
位于区间端点上的点也算作区间内。
**输入格式**
第一行包含整数 $N$,表示区间数。
接下来 $N$ 行,每行包含两个整数 $a_i,b_i$,表示一个区间的两个端点。
**输出格式**
输出一个整数,表示所需的点的最小数量。
**数据范围**
$1≤N≤10^5$,
$−10^9≤a_i≤b_i≤10^9$
**输入样例**:
```cpp {.line-numbers}
3
-1 1
2 4
3 5
```
**输出样例**:
```cpp {.line-numbers}
2
```
### 二、题目解读

- 每个线段上最少要选择一个点
- 如果一个点同时出现在两个线段上,就可以节约掉一个点
给$N$个区间,问最少可以选择几个点,上图可以选择两个点。
### 三、解题思路
贪心问题,区间问题无外乎就是排序
- 按左端点排序
- 按右端点排序
- 双关键字排序(先按右端点,再按左端点)
如果没有思路就先试一下,举一些例子,感受一下是不是有问题,看看有什么规律没有。
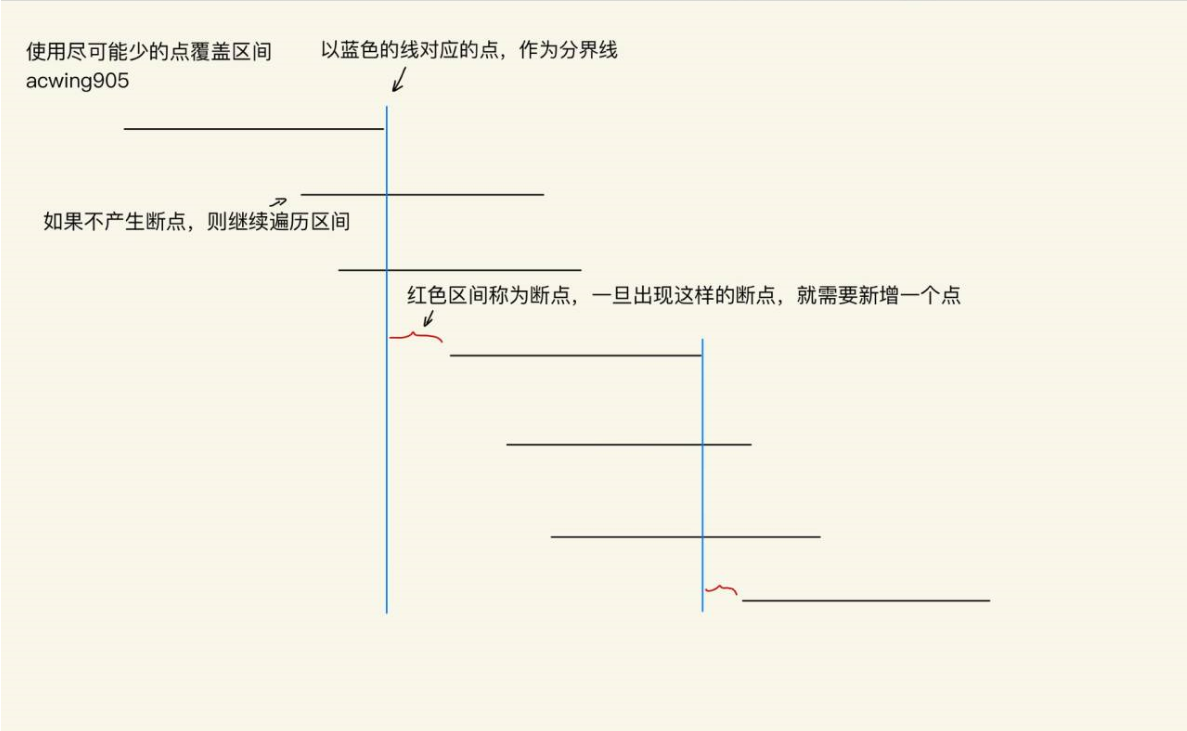 **$Q$:为啥要按右端点排序呢?**
$A$:选择右端点,就是想获取到本个线段的最大可以达到哪个位置,能获得最大的利益。
### 三、实现代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
int n; // 线段数量
int res; // 结果
int ed = -INF; // 当前覆盖区间的结束边界,即右端点位置
// 结构体
struct Node {
int l, r;
// 按每个区间的右端点从小到大排序
const bool operator<(const Node &b) const {
return r < b.r;
}
} range[N];
int main() {
cin >> n;
// 注意这里的数组下标是从0开始的
for (int i = 0; i < n; i++) cin >> range[i].l >> range[i].r;
// 右端点从小到大排序,排序也需要从数组下标1开始
sort(range, range + n);
// 思想:① 所有区间按右端点从小到大排序
//② 遍历每一个区间,如果当前区间的左与前一个区间的右有交集,则只需要一个点就可以覆盖掉两个区间
for (int i = 0; i < n; i++)
if (range[i].l > ed) {
res++;
ed = range[i].r;
}
cout << res << endl;
return 0;
}
```
### 四、$PII$简化版本
```cpp {.line-numbers}
#include
using namespace std;
#define l second
#define r first
typedef pair PII;
const int INF = 0x3f3f3f3f;
const int N = 1e5 + 10;
int n;
PII a[N];
/*
由于pair会自动以first升序排列所以用pair就不用自己重载小于运算符,至于first和second的先后关系其实没什么意义。
只要在输入/存储时交换一下x,y顺序即可,如果觉得容易混可以直接定义l为second,r为first就不会混了,同理以左端点排序的题一样
*/
int res, ed = -INF;
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
int x, y;
cin >> x >> y;
a[i] = {y, x};
}
sort(a, a + n);
for (int i = 0; i < n; i++) {
if (a[i].l > ed) {
res++;
ed = a[i].r;
}
}
cout << res << endl;
return 0;
}
```
### 五、贪心思路证明
要想看懂$Y$总的证明,关键是要弄清楚$cnt$的含义究竟是什么,其实$cnt$有两个含义:
①是指,按照各区间按右端点从小到大排,再从前往后枚举各区间,若当前区间中已包含之前被选的区间右端点,则直接跳过该区间;否则,选择当前区间的右端点这样的贪心思路所选出来的右端点的数量。
②是指,所有区间中一定存在$cnt$个两两之间没有交集的区间。因为各区间按照右端点排序后,每一个被选择的区间右端点(共$cnt$个)都是没有被 (被选择的排序位置更靠前的区间的右端点) 覆盖到的区间的 右端点。
**证明**
①假设最优解为$ans$个,以上述贪心思路选出来的点为$cnt$个。即证明$ans == cnt$,等价于证$ans >= cnt$ 同时 $ans <= cnt$
②首先,以上述贪心思路选择出的$cnt$个点,是一组可行方案。其覆盖了所有区间,满足题目要求。又因为$ans$是最优解,即为所有可行方案的最小值,那么最优解$ans <= cnt$成立
③其次由于所有区间中一定存在$cnt$个两两之间没有交集的区间,那么至少需要$cnt$个点才能将这些两两不交的区间进行覆盖,又因为题目要求选的点还要能覆盖所有别的区间,故最优解$ans >= cnt$成立
**$Q$:为啥要按右端点排序呢?**
$A$:选择右端点,就是想获取到本个线段的最大可以达到哪个位置,能获得最大的利益。
### 三、实现代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1e5 + 10;
const int INF = 0x3f3f3f3f;
int n; // 线段数量
int res; // 结果
int ed = -INF; // 当前覆盖区间的结束边界,即右端点位置
// 结构体
struct Node {
int l, r;
// 按每个区间的右端点从小到大排序
const bool operator<(const Node &b) const {
return r < b.r;
}
} range[N];
int main() {
cin >> n;
// 注意这里的数组下标是从0开始的
for (int i = 0; i < n; i++) cin >> range[i].l >> range[i].r;
// 右端点从小到大排序,排序也需要从数组下标1开始
sort(range, range + n);
// 思想:① 所有区间按右端点从小到大排序
//② 遍历每一个区间,如果当前区间的左与前一个区间的右有交集,则只需要一个点就可以覆盖掉两个区间
for (int i = 0; i < n; i++)
if (range[i].l > ed) {
res++;
ed = range[i].r;
}
cout << res << endl;
return 0;
}
```
### 四、$PII$简化版本
```cpp {.line-numbers}
#include
using namespace std;
#define l second
#define r first
typedef pair PII;
const int INF = 0x3f3f3f3f;
const int N = 1e5 + 10;
int n;
PII a[N];
/*
由于pair会自动以first升序排列所以用pair就不用自己重载小于运算符,至于first和second的先后关系其实没什么意义。
只要在输入/存储时交换一下x,y顺序即可,如果觉得容易混可以直接定义l为second,r为first就不会混了,同理以左端点排序的题一样
*/
int res, ed = -INF;
int main() {
cin >> n;
for (int i = 0; i < n; i++) {
int x, y;
cin >> x >> y;
a[i] = {y, x};
}
sort(a, a + n);
for (int i = 0; i < n; i++) {
if (a[i].l > ed) {
res++;
ed = a[i].r;
}
}
cout << res << endl;
return 0;
}
```
### 五、贪心思路证明
要想看懂$Y$总的证明,关键是要弄清楚$cnt$的含义究竟是什么,其实$cnt$有两个含义:
①是指,按照各区间按右端点从小到大排,再从前往后枚举各区间,若当前区间中已包含之前被选的区间右端点,则直接跳过该区间;否则,选择当前区间的右端点这样的贪心思路所选出来的右端点的数量。
②是指,所有区间中一定存在$cnt$个两两之间没有交集的区间。因为各区间按照右端点排序后,每一个被选择的区间右端点(共$cnt$个)都是没有被 (被选择的排序位置更靠前的区间的右端点) 覆盖到的区间的 右端点。
**证明**
①假设最优解为$ans$个,以上述贪心思路选出来的点为$cnt$个。即证明$ans == cnt$,等价于证$ans >= cnt$ 同时 $ans <= cnt$
②首先,以上述贪心思路选择出的$cnt$个点,是一组可行方案。其覆盖了所有区间,满足题目要求。又因为$ans$是最优解,即为所有可行方案的最小值,那么最优解$ans <= cnt$成立
③其次由于所有区间中一定存在$cnt$个两两之间没有交集的区间,那么至少需要$cnt$个点才能将这些两两不交的区间进行覆盖,又因为题目要求选的点还要能覆盖所有别的区间,故最优解$ans >= cnt$成立

