## [$AcWing$ $1175$. 最大半连通子图 ](https://www.acwing.com/problem/content/1177/)
### 一、题目描述
一个有向图 $G=(V,E)$ 称为半连通的 ($Semi-Connected$),如果满足:$∀u,v∈V$,满足 $u→v$ 或 $v→u$,即对于图中任意两点 $u,v$,存在一条 $u$ 到 $v$ 的有向路径或者从 $v$ 到 $u$ 的有向路径。
若 $G'=(V',E')$ 满足,$E'$ 是 $E$ 中所有和 $V'$ 有关的边,则称 $G'$ 是 $G$ 的一个导出子图。
若 $G'$ 是 $G$ 的导出子图,且 $G'$ 半连通,则称 $G'$ 为 $G$ 的半连通子图。
若 $G'$ 是 $G$ 所有半连通子图中包含节点数最多的,则称 $G'$ 是 $G$ 的最大半连通子图。
给定一个有向图 $G$,请求出 $G$ 的最大半连通子图拥有的节点数 $K$,以及不同的最大半连通子图的数目 $C$。
由于 $C$ 可能比较大,仅要求输出 $C$ 对 $X$ 的余数。
**输入格式**
第一行包含三个整数 $N,M,X$。$N,M$ 分别表示图 $G$ 的点数与边数,$X$ 的意义如上文所述;
接下来 $M$ 行,每行两个正整数 $a,b$,表示一条有向边 $(a,b)$。
图中的每个点将编号为 $1$ 到 $N$,保证输入中同一个 $(a,b)$ 不会出现两次。
**输出格式**
应包含两行。
第一行包含一个整数 $K$,第二行包含整数 $C$ $mod$ $X$。
**数据范围**
$1≤N≤10^5,1≤M≤10^6,1≤X≤10^8$
**输入样例**:
```cpp {.line-numbers}
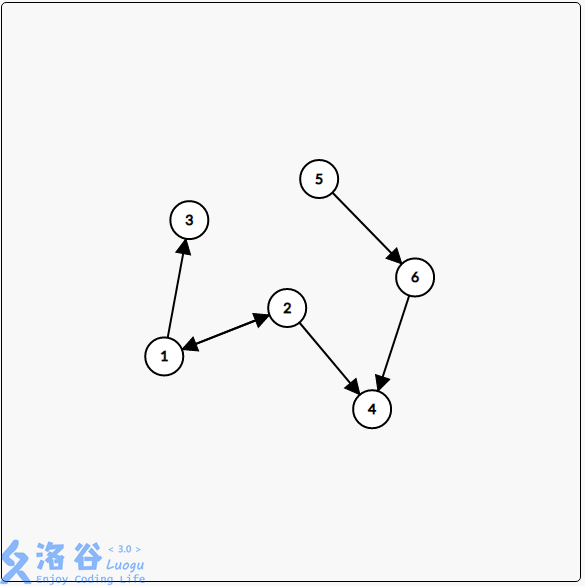
6 6 20070603
1 2
2 1
1 3
2 4
5 6
6 4
```
**输出样例**:
```cpp {.line-numbers}
3
3
```
### 二、前导知识
#### 1、强连通分量
 > 有向图的 **极大强连通子图**,称为 **强连通分量**($strongly$ $connected$ $components$)。
> 在有向图$G$中,如果两个顶点$v_i,v_j$间($v_i>v_j$)有一条从$v_i$到$v_j$的有向路径,同时还有一条从$v_j$到$v_i$的有向路径,则称 **两个顶点强连通**($strongly$ $connected$)。如果有向图$G$的 **每两个顶点都强连通**,称$G$是一个 **强连通图**。
#### 2、半连通子图
> 有向图的 **极大强连通子图**,称为 **强连通分量**($strongly$ $connected$ $components$)。
> 在有向图$G$中,如果两个顶点$v_i,v_j$间($v_i>v_j$)有一条从$v_i$到$v_j$的有向路径,同时还有一条从$v_j$到$v_i$的有向路径,则称 **两个顶点强连通**($strongly$ $connected$)。如果有向图$G$的 **每两个顶点都强连通**,称$G$是一个 **强连通图**。
#### 2、半连通子图
 ### 三、解题思路
还是先从拓扑图$DAG$的角度来思考,毕竟不是$DAG$我们也可以用$Tarjan$把它缩点成$DAG$。
在一张图上,一个强连通分量必定是半连通子图,一条链上的若干个强连通分量,也必定可以构成半连通子图,为什么?假设是这样一个串
$$A_1⇒A_2⇒A_3⇒A_4⇒A_5⇒A_6$$
从$A_1$到$A_2$是必定存在一条有某个分界点$u∈A_1$和另一个点$v∈A_2$之间有一条边,只要这样我们就可以保证$A_1$和$A_2$可以构成半连通子图(因为强连通分量内每个点都是 **有关系的** )
因而可以推出$A_2$和$A_3$也可以构成半连通子图,因此整条链都可以构成半连通子图。
所以我们这道题尽量跑长一点的链,这样我们最后构成的半连通子图才会 **尽量大**
因为已经是拓扑图,我们就可以通过拓扑序$DP$,这样就可以很容易地得到它的最长链,顺便也可以统计出方案数,通过加法原理就可以得到下列方程
- ① 当$f[u]=0$,也就是没有被更新过的时候
$$\large f[u]=sz[u],g[u]=1$$
- ② 当$f[v]**解释**:所有从走到$u$的,再从$u$走到$v$是唯一的
- ③ 当$f[v]=f[u]+sz[v]$(发现一样长的链一起选)
$$\large g[v]+=g[u] \% mod$$
>**解释**:顺便取模
这边我们半连通子图的大小应该是整条链上所有的强连通分量内点的个数和,然后跑最长链,就行了。
#### 总结
- ① 核心思想就是$tarjan$后缩点,建新的$DAG$图
- ② 这个$DAG$是有点权的,点权就是$SCC$的大小
- ③ 跑完$tarjan$以后$SCC$编号的 **逆序** 就是$DAG$的拓扑序
- ④ 在$DAG$上通过 **拓扑序** 递推,不断更新 **点权和 最长路径$f[N]$**,以及这个路径的方案数量(副产品)$g[N]$
#### 坑
- 这里新建的$DAG$的边是要 **去重** 的,因为缩点以后可能有重边,根据半联通子图定义这些重边必须都取
### 四、实现代码
```cpp {.line-numbers}
#include
using namespace std;
typedef long long LL;
const int N = 100010, M = 2000010; // 因为要建新图,两倍的边
int n, m, mod; // 点数、边数、取模的数
int f[N], g[N];
int h[N], hs[N], e[M], ne[M], idx; // h: 原图;hs: 新图
void add(int h[], int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// tarjan求强连通分量
int dfn[N], low[N], ts, in_stk[N], stk[N], top;
int id[N], scc_cnt, sz[N];
void tarjan(int u) {
dfn[u] = low[u] = ++ts;
stk[++top] = u;
in_stk[u] = 1;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (in_stk[v])
low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) {
++scc_cnt;
int x;
do {
x = stk[top--];
in_stk[x] = 0;
id[x] = scc_cnt;
sz[scc_cnt]++;
} while (x != u);
}
}
int main() {
memset(h, -1, sizeof h); // 原图
memset(hs, -1, sizeof hs); // 新图
scanf("%d %d %d", &n, &m, &mod);
while (m--) {
int a, b;
scanf("%d %d", &a, &b);
add(h, a, b);
}
// (1) tarjan算法求强连通分量
for (int i = 1; i <= n; i++)
if (!dfn[i]) tarjan(i);
// (2) 缩点,建新图
unordered_set S; // 对连着两个不同强连通分量的边进行判重
for (int u = 1; u <= n; u++)
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
int a = id[u], b = id[v];
LL hash = a * 1000000ll + b; // 新两点a,b之间的Hash值,防止出现重边
if (a != b && !S.count(hash)) { // ① 不同的连通块 ② 非重边
add(hs, a, b); // 加入新图
S.insert(hash); // 记录a,b端点的边使用过
}
}
// (3) tarjan统计出来的前连通分量是逆拓扑序的
// 计算以每个新点(强连通分量)为终点的最长链中的点的数目f[i]和数量g[i]
for (int u = scc_cnt; u; u--) { // 因此dp的初始点就在id的最后一个,因此我们逆着id做就是拓扑序了
if (!f[u]) { // u节点被初次访问时
f[u] = sz[u]; // 最长链中点数量=存储u号强连通分量中节点的个数
g[u] = 1; // 最长链的条数=1条
}
// 对DAG开始进行递推,层次感好强
for (int i = hs[u]; ~i; i = ne[i]) {
int v = e[i];
if (f[v] < f[u] + sz[v]) {
f[v] = f[u] + sz[v]; // 最大值被打破(联想数字三角形)
g[v] = g[u]; // 同步更新条数
} else if (f[v] == f[u] + sz[v]) // 最大值被追平,则叠加条数
g[v] = (g[v] + g[u]) % mod;
}
}
// (4) 求解答案
int res = 0, sum = 0; // 最大半连通子图节点数、对应方案数
for (int i = 1; i <= scc_cnt; i++)
if (f[i] > res)
res = f[i], sum = g[i];
else if (f[i] == res)
sum = (sum + g[i]) % mod;
// 输出
printf("%d\n%d\n", res, sum);
return 0;
}
```
### 五、答疑解惑
#### $Q1$:为什么在缩点全新建图过程中,需要去重边?

测试样例:
```cpp {.line-numbers}
4 6
1 2
2 1
3 4
4 3
1 3
2 3
```
测试代码:
```cpp {.line-numbers}
#include
using namespace std;
const int N = 100010, M = 2000010; // 因为要建新图,两倍的边
int n, m, mod; // 点数、边数、取模的数
int f[N], g[N];
int h[N], hs[N], e[M], ne[M], idx; // h: 原图;hs: 新图
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// tarjan求强连通分量
int dfn[N], low[N], ts, in_stk[N], stk[N], top;
int id[N], scc_cnt, sz[N];
void tarjan(int u) {
dfn[u] = low[u] = ++ts;
stk[++top] = u;
in_stk[u] = 1;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (in_stk[v])
low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) {
++scc_cnt;
int x;
do {
x = stk[top--];
in_stk[x] = 0;
id[x] = scc_cnt;
sz[scc_cnt]++;
} while (x != u);
}
}
int main() {
#ifndef ONLINE_JUDGE
freopen("1175_Preapre.in", "r", stdin);
#endif
memset(h, -1, sizeof h); // 原图
scanf("%d %d", &n, &m);
while (m--) {
int a, b;
scanf("%d %d", &a, &b);
add(a, b);
}
// (1) tarjan算法求强连通分量
for (int i = 1; i <= n; i++)
if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; i++)
cout << "id[" << i << "]=" << id[i] << " ";
cout << endl;
cout << "scc_cnt=" << scc_cnt << endl;
return 0;
}
```
#### $Q2:$ 为什么倒序枚举$scc\_cnt$就是拓扑序
**答**:$tarjan$ 拓扑排序就是$scc$逆序,这是性质。原因是$tarjan$是递归写法,先子节点后父节点
### 三、解题思路
还是先从拓扑图$DAG$的角度来思考,毕竟不是$DAG$我们也可以用$Tarjan$把它缩点成$DAG$。
在一张图上,一个强连通分量必定是半连通子图,一条链上的若干个强连通分量,也必定可以构成半连通子图,为什么?假设是这样一个串
$$A_1⇒A_2⇒A_3⇒A_4⇒A_5⇒A_6$$
从$A_1$到$A_2$是必定存在一条有某个分界点$u∈A_1$和另一个点$v∈A_2$之间有一条边,只要这样我们就可以保证$A_1$和$A_2$可以构成半连通子图(因为强连通分量内每个点都是 **有关系的** )
因而可以推出$A_2$和$A_3$也可以构成半连通子图,因此整条链都可以构成半连通子图。
所以我们这道题尽量跑长一点的链,这样我们最后构成的半连通子图才会 **尽量大**
因为已经是拓扑图,我们就可以通过拓扑序$DP$,这样就可以很容易地得到它的最长链,顺便也可以统计出方案数,通过加法原理就可以得到下列方程
- ① 当$f[u]=0$,也就是没有被更新过的时候
$$\large f[u]=sz[u],g[u]=1$$
- ② 当$f[v]**解释**:所有从走到$u$的,再从$u$走到$v$是唯一的
- ③ 当$f[v]=f[u]+sz[v]$(发现一样长的链一起选)
$$\large g[v]+=g[u] \% mod$$
>**解释**:顺便取模
这边我们半连通子图的大小应该是整条链上所有的强连通分量内点的个数和,然后跑最长链,就行了。
#### 总结
- ① 核心思想就是$tarjan$后缩点,建新的$DAG$图
- ② 这个$DAG$是有点权的,点权就是$SCC$的大小
- ③ 跑完$tarjan$以后$SCC$编号的 **逆序** 就是$DAG$的拓扑序
- ④ 在$DAG$上通过 **拓扑序** 递推,不断更新 **点权和 最长路径$f[N]$**,以及这个路径的方案数量(副产品)$g[N]$
#### 坑
- 这里新建的$DAG$的边是要 **去重** 的,因为缩点以后可能有重边,根据半联通子图定义这些重边必须都取
### 四、实现代码
```cpp {.line-numbers}
#include
using namespace std;
typedef long long LL;
const int N = 100010, M = 2000010; // 因为要建新图,两倍的边
int n, m, mod; // 点数、边数、取模的数
int f[N], g[N];
int h[N], hs[N], e[M], ne[M], idx; // h: 原图;hs: 新图
void add(int h[], int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// tarjan求强连通分量
int dfn[N], low[N], ts, in_stk[N], stk[N], top;
int id[N], scc_cnt, sz[N];
void tarjan(int u) {
dfn[u] = low[u] = ++ts;
stk[++top] = u;
in_stk[u] = 1;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (in_stk[v])
low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) {
++scc_cnt;
int x;
do {
x = stk[top--];
in_stk[x] = 0;
id[x] = scc_cnt;
sz[scc_cnt]++;
} while (x != u);
}
}
int main() {
memset(h, -1, sizeof h); // 原图
memset(hs, -1, sizeof hs); // 新图
scanf("%d %d %d", &n, &m, &mod);
while (m--) {
int a, b;
scanf("%d %d", &a, &b);
add(h, a, b);
}
// (1) tarjan算法求强连通分量
for (int i = 1; i <= n; i++)
if (!dfn[i]) tarjan(i);
// (2) 缩点,建新图
unordered_set S; // 对连着两个不同强连通分量的边进行判重
for (int u = 1; u <= n; u++)
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
int a = id[u], b = id[v];
LL hash = a * 1000000ll + b; // 新两点a,b之间的Hash值,防止出现重边
if (a != b && !S.count(hash)) { // ① 不同的连通块 ② 非重边
add(hs, a, b); // 加入新图
S.insert(hash); // 记录a,b端点的边使用过
}
}
// (3) tarjan统计出来的前连通分量是逆拓扑序的
// 计算以每个新点(强连通分量)为终点的最长链中的点的数目f[i]和数量g[i]
for (int u = scc_cnt; u; u--) { // 因此dp的初始点就在id的最后一个,因此我们逆着id做就是拓扑序了
if (!f[u]) { // u节点被初次访问时
f[u] = sz[u]; // 最长链中点数量=存储u号强连通分量中节点的个数
g[u] = 1; // 最长链的条数=1条
}
// 对DAG开始进行递推,层次感好强
for (int i = hs[u]; ~i; i = ne[i]) {
int v = e[i];
if (f[v] < f[u] + sz[v]) {
f[v] = f[u] + sz[v]; // 最大值被打破(联想数字三角形)
g[v] = g[u]; // 同步更新条数
} else if (f[v] == f[u] + sz[v]) // 最大值被追平,则叠加条数
g[v] = (g[v] + g[u]) % mod;
}
}
// (4) 求解答案
int res = 0, sum = 0; // 最大半连通子图节点数、对应方案数
for (int i = 1; i <= scc_cnt; i++)
if (f[i] > res)
res = f[i], sum = g[i];
else if (f[i] == res)
sum = (sum + g[i]) % mod;
// 输出
printf("%d\n%d\n", res, sum);
return 0;
}
```
### 五、答疑解惑
#### $Q1$:为什么在缩点全新建图过程中,需要去重边?

测试样例:
```cpp {.line-numbers}
4 6
1 2
2 1
3 4
4 3
1 3
2 3
```
测试代码:
```cpp {.line-numbers}
#include
using namespace std;
const int N = 100010, M = 2000010; // 因为要建新图,两倍的边
int n, m, mod; // 点数、边数、取模的数
int f[N], g[N];
int h[N], hs[N], e[M], ne[M], idx; // h: 原图;hs: 新图
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
// tarjan求强连通分量
int dfn[N], low[N], ts, in_stk[N], stk[N], top;
int id[N], scc_cnt, sz[N];
void tarjan(int u) {
dfn[u] = low[u] = ++ts;
stk[++top] = u;
in_stk[u] = 1;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
} else if (in_stk[v])
low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) {
++scc_cnt;
int x;
do {
x = stk[top--];
in_stk[x] = 0;
id[x] = scc_cnt;
sz[scc_cnt]++;
} while (x != u);
}
}
int main() {
#ifndef ONLINE_JUDGE
freopen("1175_Preapre.in", "r", stdin);
#endif
memset(h, -1, sizeof h); // 原图
scanf("%d %d", &n, &m);
while (m--) {
int a, b;
scanf("%d %d", &a, &b);
add(a, b);
}
// (1) tarjan算法求强连通分量
for (int i = 1; i <= n; i++)
if (!dfn[i]) tarjan(i);
for (int i = 1; i <= n; i++)
cout << "id[" << i << "]=" << id[i] << " ";
cout << endl;
cout << "scc_cnt=" << scc_cnt << endl;
return 0;
}
```
#### $Q2:$ 为什么倒序枚举$scc\_cnt$就是拓扑序
**答**:$tarjan$ 拓扑排序就是$scc$逆序,这是性质。原因是$tarjan$是递归写法,先子节点后父节点


