##[$AcWing$ $890$. 能被整除的数](https://www.acwing.com/problem/content/892/)
### 一、题目描述
给定一个整数 $n$ 和 $m$ 个不同的质数 $p_1,p_2,…,p_m$。
请你求出 $1$∼$n$ 中能被 $p_1,p_2,…,p_m$ 中的 **至少一个数整除的整数** 有多少个。
**输入格式**
第一行包含整数 $n$ 和 $m$。
第二行包含 $m$ 个质数。
**输出格式**
输出一个整数,表示满足条件的整数的个数。
**数据范围**
$1≤m≤16,1≤n,p_i≤10^9$
**输入样例:**
```cpp {.line-numbers}
10 2
2 3
```
**输出样例:**
```cpp {.line-numbers}
7
```
### 二、理论知识
韦恩图(又称文氏图)
#### (1)两个圆相交求面积
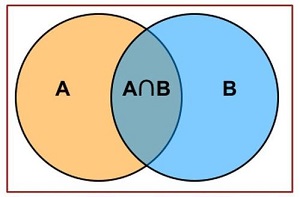 $$\large S=S_1+S_2-S_1\cap S_2$$
#### (2)三个圆相交求面积
$$\large S=S_1+S_2-S_1\cap S_2$$
#### (2)三个圆相交求面积
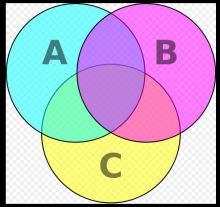 $$\large S=S_1+S_2+S_3- S_1\cap S_2 -S_2\cap S_3 - S_1\cap S_3 + S_1\cap S_2 \cap S_3$$
#### (3)四个圆相交求面积
$$\large S=S_1+S_2+S_3- S_1\cap S_2 -S_2\cap S_3 - S_1\cap S_3 + S_1\cap S_2 \cap S_3$$
#### (3)四个圆相交求面积
 $$\large S=S_1+S_2 + S_3 + S_4 -S_1\cap S_2 -S_1\cap S_3 -S_1\cap S_4 - S_2\cap S_3 -S_2\cap S_4 -S_3\cap S_4 + S_1\cap S_2 \cap S_3 + S_1\cap S_2 \cap S_4+ S_2\cap S_3 \cap S_4 ++ S_1\cap S_3 \cap S_4 - S_1 \cap S_2 \cap S_3 \cap S_4$$
上面,我们是用面积来考虑的问题,所以等式左边写的是$S$,也可以用集合来考虑,以$3$个圆为例,那就是
$|S_1 \cup S_2 \cup S_3| =|S_1|+|S_2|+|S_3|- |S_1\cap S_2| -|S_2\cap S_3| - |S_1\cap S_3| + |S_1\cap S_2 \cap S_3|$
其中$||$**代表集合中的元素个数**。
#### (4)规律总结
上面的求解过程,其实是在求 $C_n^1 - C_n^2+ ... + {(-1)}^{n-1}C_n^n$,
也就理解为从$n$个选择1个,减去从$n$中选择$2$个,加上从$n$中选择$3$个,减去从$n$中减去$4$个...,也可以记为奇数个元素的集合是加,偶数个的(指相交)的集合是减。
#### (5)经典例题
容斥原理有个经典题目:一个班每个人都有自己喜欢的科目:
* $20$人喜欢数学,$10$人喜欢语文,$11$人喜欢英语;
* $3$人同时喜欢数学语文,$3$人同时喜欢语文英语,$4$人同时喜欢数学英语
* $2$人都喜欢
问全班有多少人?
根据容斥原理,就是$\large S=S_1+S_2+S_3- S_1\cap S_2 -S_2\cap S_3 - S_1\cap S_3 + S_1\cap S_2 \cap S_3$
班级人数=$20+10+11-3-3-4+2=33$
### 三、本题思路
**数学表达式**
比如三个质数是$2,3,5$,$S_2$代表$2$的倍数集合,$S_3$代表$3$的倍数集合,$S_5$代表$5$的倍数集合,至少能被其中一个质数整除的总个数就是:
$|S_2 \cup S_3 \cup S_5| = |S_2| + |S_3| +|S_5| -|S_2 \cap S_3| -|S_3 \cap S_5| -|S_2 \cap S_5|+|S_2 \cap S_3 \cap S_5|$
> 解释:上面表示式中$|S_2|$代表的是: $2$的倍数集合的数字个数
* **$Q1$:如何计算$|S_p|$这样的表达式数值?**
$|S_p|$:**计算小于等于$n$中能整除掉$p$的数字个数** $\huge \lfloor \frac{n}{p} \rfloor$,$C++$默认就是下取整,不用再特殊处理。
* **$Q2$:如何计算$|S_2 \cap S_3|$这样的表达式值?**
题目给定的$p_i$都是质数,所以能被$2$整除,也能被$3$整除的数,肯定是能被$6$整除的数,所以就是 $|S_6|=|S_2 \cap S_3|$,这样,问题就转化成了问题$|S_p|$,也就会求解了!
* **$Q3$:怎么把这些子项目都罗列出来?**
其实罗列的是$p[i]$的所有组合方式!举个栗子: $\{2\},\{3\},\{5\},\{2,3\},\{3,5\},\{2,5\},\{2,3,5\}$共$7$种,也就是$2^3-1=7$种。
**常用技巧:二进制数位枚举**

**举个栗子:**
```cpp {.line-numbers}
#include
using namespace std;
#define int long long
#define endl "\n"
int n, m; // n:质数个数,m:1~m的数字中有多少个可以被质数序列中至少一个整数整除。
// 注意:代码里的n,m与模板题目中的含义相反!一定要注意!!!!!!!!!!!!
vector p; // 质数数组
signed main() {
cin >> m >> n; // 与m互质,n个质数!
// 读入n个质数,为了使用vector,读入时确实不太方便
for (int i = 0; i < n; i++) {
int x;
cin >> x;
p.push_back(x);
}
// ① 枚举从1到 2^n-1,每个数字,代表一种状态,每个状态代表一种质数的挑选办法
// 当然,这些整数值的乘积可能大于n,大于的没用,只要小于等于n的
int s = 0;
for (int i = 1; i < 1 << p.size(); i++) {
int t = 1, cnt = 0; // 累乘积,质因子个数
// ② 在对应的整数值确定后,枚举此数值的每一个数位
for (int j = 0; j < p.size(); j++)
if (i >> j & 1) { // ③判断当前数位是不是1,是1表示当前数位选中
if (t * p[j] > m) { // 乘积不能超过最大值m,控制在[1~m]范围内
t = 0; // s=0代表本次挑选的组合失败,无效
break; // 由于i是由小到大遍历的,前面的都无效了,后面的肯定更大,更无效,不用继续了
}
cnt++; // 选择的质因子个数
t *= p[j]; // 累乘积
}
if (t) { // 超过范围的,s=0,所以,现在代表只讨论在范围内的
if (cnt & 1) // 质数因子数量,奇数加
s += m / t; // 引理内容,代表m里面有多少个这个数字s的倍数
else // 偶数减
s -= m / t;
}
}
cout << s << endl;
}
```
$$\large S=S_1+S_2 + S_3 + S_4 -S_1\cap S_2 -S_1\cap S_3 -S_1\cap S_4 - S_2\cap S_3 -S_2\cap S_4 -S_3\cap S_4 + S_1\cap S_2 \cap S_3 + S_1\cap S_2 \cap S_4+ S_2\cap S_3 \cap S_4 ++ S_1\cap S_3 \cap S_4 - S_1 \cap S_2 \cap S_3 \cap S_4$$
上面,我们是用面积来考虑的问题,所以等式左边写的是$S$,也可以用集合来考虑,以$3$个圆为例,那就是
$|S_1 \cup S_2 \cup S_3| =|S_1|+|S_2|+|S_3|- |S_1\cap S_2| -|S_2\cap S_3| - |S_1\cap S_3| + |S_1\cap S_2 \cap S_3|$
其中$||$**代表集合中的元素个数**。
#### (4)规律总结
上面的求解过程,其实是在求 $C_n^1 - C_n^2+ ... + {(-1)}^{n-1}C_n^n$,
也就理解为从$n$个选择1个,减去从$n$中选择$2$个,加上从$n$中选择$3$个,减去从$n$中减去$4$个...,也可以记为奇数个元素的集合是加,偶数个的(指相交)的集合是减。
#### (5)经典例题
容斥原理有个经典题目:一个班每个人都有自己喜欢的科目:
* $20$人喜欢数学,$10$人喜欢语文,$11$人喜欢英语;
* $3$人同时喜欢数学语文,$3$人同时喜欢语文英语,$4$人同时喜欢数学英语
* $2$人都喜欢
问全班有多少人?
根据容斥原理,就是$\large S=S_1+S_2+S_3- S_1\cap S_2 -S_2\cap S_3 - S_1\cap S_3 + S_1\cap S_2 \cap S_3$
班级人数=$20+10+11-3-3-4+2=33$
### 三、本题思路
**数学表达式**
比如三个质数是$2,3,5$,$S_2$代表$2$的倍数集合,$S_3$代表$3$的倍数集合,$S_5$代表$5$的倍数集合,至少能被其中一个质数整除的总个数就是:
$|S_2 \cup S_3 \cup S_5| = |S_2| + |S_3| +|S_5| -|S_2 \cap S_3| -|S_3 \cap S_5| -|S_2 \cap S_5|+|S_2 \cap S_3 \cap S_5|$
> 解释:上面表示式中$|S_2|$代表的是: $2$的倍数集合的数字个数
* **$Q1$:如何计算$|S_p|$这样的表达式数值?**
$|S_p|$:**计算小于等于$n$中能整除掉$p$的数字个数** $\huge \lfloor \frac{n}{p} \rfloor$,$C++$默认就是下取整,不用再特殊处理。
* **$Q2$:如何计算$|S_2 \cap S_3|$这样的表达式值?**
题目给定的$p_i$都是质数,所以能被$2$整除,也能被$3$整除的数,肯定是能被$6$整除的数,所以就是 $|S_6|=|S_2 \cap S_3|$,这样,问题就转化成了问题$|S_p|$,也就会求解了!
* **$Q3$:怎么把这些子项目都罗列出来?**
其实罗列的是$p[i]$的所有组合方式!举个栗子: $\{2\},\{3\},\{5\},\{2,3\},\{3,5\},\{2,5\},\{2,3,5\}$共$7$种,也就是$2^3-1=7$种。
**常用技巧:二进制数位枚举**

**举个栗子:**
```cpp {.line-numbers}
#include
using namespace std;
#define int long long
#define endl "\n"
int n, m; // n:质数个数,m:1~m的数字中有多少个可以被质数序列中至少一个整数整除。
// 注意:代码里的n,m与模板题目中的含义相反!一定要注意!!!!!!!!!!!!
vector p; // 质数数组
signed main() {
cin >> m >> n; // 与m互质,n个质数!
// 读入n个质数,为了使用vector,读入时确实不太方便
for (int i = 0; i < n; i++) {
int x;
cin >> x;
p.push_back(x);
}
// ① 枚举从1到 2^n-1,每个数字,代表一种状态,每个状态代表一种质数的挑选办法
// 当然,这些整数值的乘积可能大于n,大于的没用,只要小于等于n的
int s = 0;
for (int i = 1; i < 1 << p.size(); i++) {
int t = 1, cnt = 0; // 累乘积,质因子个数
// ② 在对应的整数值确定后,枚举此数值的每一个数位
for (int j = 0; j < p.size(); j++)
if (i >> j & 1) { // ③判断当前数位是不是1,是1表示当前数位选中
if (t * p[j] > m) { // 乘积不能超过最大值m,控制在[1~m]范围内
t = 0; // s=0代表本次挑选的组合失败,无效
break; // 由于i是由小到大遍历的,前面的都无效了,后面的肯定更大,更无效,不用继续了
}
cnt++; // 选择的质因子个数
t *= p[j]; // 累乘积
}
if (t) { // 超过范围的,s=0,所以,现在代表只讨论在范围内的
if (cnt & 1) // 质数因子数量,奇数加
s += m / t; // 引理内容,代表m里面有多少个这个数字s的倍数
else // 偶数减
s -= m / t;
}
}
cout << s << endl;
}
```


