##  [$AcWing$ $1146$. 新的开始](https://www.acwing.com/problem/content/description/1148/)

### 一、题目描述
发展采矿业当然首先得有矿井，小 $FF$ 花了上次探险获得的千分之一的财富请人在岛上挖了 $n$ 口矿井，但他似乎忘记了考虑矿井供电问题。

为了保证电力的供应，小 $FF$ 想到了两种办法：

在矿井 $i$ 上建立一个发电站，费用为 $v_i$（发电站的输出功率可以供给任意多个矿井）。
将这口矿井 $i$ 与另外的已经有电力供应的矿井 $j$ 之间建立电网，费用为 $p_{i,j}$。
小 $FF$ 希望你帮他想出一个保证所有矿井电力供应的 **最小花费方案**。

**输入格式**
第一行包含一个整数 $n$，表示矿井总数。

接下来 $n$ 行，每行一个整数，第 $i$ 个数 $v_i$ 表示在第 $i$ 口矿井上建立发电站的费用。

接下来为一个 $n×n$ 的矩阵 $P$，其中 $p_{i,j}$ 表示在第 $i$ 口矿井和第 $j$ 口矿井之间建立电网的费用。

数据保证 $p_{i,j}=p_{j,i}$，且 $p_{i,i}=0$。

**输出格式**
输出一个整数，表示让所有矿井获得充足电能的最小花费。

**数据范围**
$1≤n≤300,0≤v_i,p_i,j≤10^5$

**输入样例**：
```cpp {.line-numbers}
4
5
4
4
3
0 2 2 2
2 0 3 3
2 3 0 4
2 3 4 0
```

**输出样例**：
```cpp {.line-numbers}
9
```

### 二、解题思路 

为了节点$i$供应电力，有两种办法：
- 在节点 $i$ 建发电站，代价为$v_i$
- 与另外的已经有电力供应的矿井 $j$ 之间建立电网,代价为$p_{i,j}$

上面两种情况，第一个是 **点权**，第二个是 **边权**,不太好统一口径，这种问题的 **经典作法** 是: 
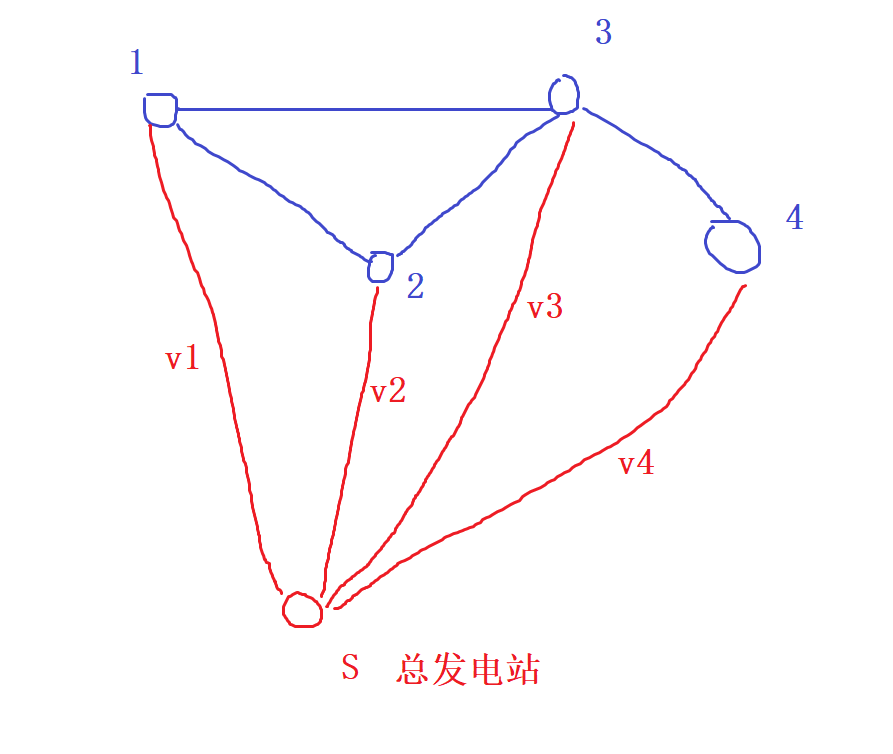
<font color='red' size=4><b>利用超级源点将点权转化为超级源点到当前点的边权</b></font>！

* 在节点$i$建发电站的费用是$v_i$,建立虚拟结点$S$，相当于$i$号点到$S$号点的费用是$v_i$

*  求$n$个矿井电力供应的最小花费，等价于求$n + 1$个点的最小生成树

![](https://cdn.acwing.com/media/article/image/2020/02/18/7416_df0277e252-f2b38c25a657be186079a431b97bf62.png)


### 三、$Kruskal$算法
```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;
const int N = 310;
const int INF = 0x3f3f3f3f;
int n;   // n条顶点
int res; // 最小生成树的权值和
int el;  // 边数
// Kruskal用到的结构体
const int M = 2 * N * N; // 无向图*2，稠密图N*N
struct Edge {
    int a, b, w;
    const bool operator<(const Edge &t) const {
        return w < t.w;
    }
} e[M];
// 并查集
int p[N];
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}
// Kruskal算法
int kruskal() {
    // 按边的权重排序
    sort(e, e + el);
    // 初始化并查集,注意并查集的初始是从0开始的，因为0号是超级源点
    for (int i = 0; i <= n; i++) p[i] = i;
    // 枚举每条边
    for (int i = 0; i < el; i++) {
        int a = e[i].a, b = e[i].b, w = e[i].w;
        a = find(a), b = find(b);
        if (a != b)
            p[a] = b, res += w;
    }
    return res;
}

int main() {
    cin >> n;
    // 建立超级源点(0 <-> 1~n )
    int w;
    for (int i = 1; i <= n; i++) {
        cin >> w; // 点权
        e[el++] = {0, i, w};
        e[el++] = {i, 0, w};
    }

    // 本题是按矩阵读入的，不是按a,b,c方式读入的
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) {
            cin >> w;
            e[el++] = {i, j, w};
            e[el++] = {j, i, w};
        }

    // 利用Kruskal计算最小生成树
    printf("%d\n", kruskal());

    return 0;
}
```

### 四、$Prim$算法
```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;

const int N = 310;

int n;
int g[N][N];
int dist[N];
bool st[N];
int res; // 最小生成树里面边的长度之和

int prim() {
    memset(dist, 0x3f, sizeof dist); // 初始化所有距离为INF
    dist[0] = 0;                     // 超级源点是在生成树中的

    for (int i = 0; i <= n; i++) { // 注意：这里因为引入了超级源点，所以点的个数是n+1
        int t = -1;
        for (int j = 0; j <= n; j++)
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        st[t] = true;
        res += dist[t];
        // 有超级源点的题，是必然存在最小生成树的
        // 注意这里也是需要从0~n共n+1个
        for (int j = 0; j <= n; j++) dist[j] = min(dist[j], g[t][j]);
    }
    return res;
}

int main() {
    cin >> n;
    // 建立超级源点(0 <-> 1~n )，点权转化为超级源点到此节点的边权
    for (int i = 1; i <= n; i++) {
        cin >> g[0][i];
        g[i][0] = g[0][i];
    }
    // 本题是按矩阵读入的，不是按a,b,c方式读入的
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            cin >> g[i][j];

    // 利用prim计算最小生成树
    printf("%d\n", prim());

    return 0;
}
```