## [$AcWing$ $1145$. 北极通讯网络](https://www.acwing.com/problem/content/1147/)

### 一、题目描述
北极的某区域共有 $n$ 座村庄，每座村庄的坐标用一对整数 $(x,y)$ 表示。

为了加强联系，决定在村庄之间建立通讯网络，使每两座村庄之间都可以 **直接** 或 **间接** 通讯。

通讯工具可以是无线电收发机，也可以是卫星设备。

无线电收发机有多种不同型号，不同型号的无线电收发机有一个不同的参数 $d$，两座村庄之间的距离如果不超过 $d$，就可以用该型号的无线电收发机直接通讯，$d$ 值越大的型号价格越贵。现在要先选择某一种型号的无线电收发机，然后统一给所有村庄配备，数量不限，但型号都是 **相同的**。

**配备卫星设备的两座村庄** 无论相距多远都可以直接通讯，但卫星设备是 **有限** 的，只能给一部分村庄配备。

现在有 $k$ 台卫星设备，请你编一个程序，计算出应该如何分配这 $k$ 台卫星设备，才能使所配备的无线电收发机的 $d$ 值最小。

例如，对于下面三座村庄：

![](https://cdn.acwing.com/media/article/image/2019/11/08/19_61a45e3c01-1.png)

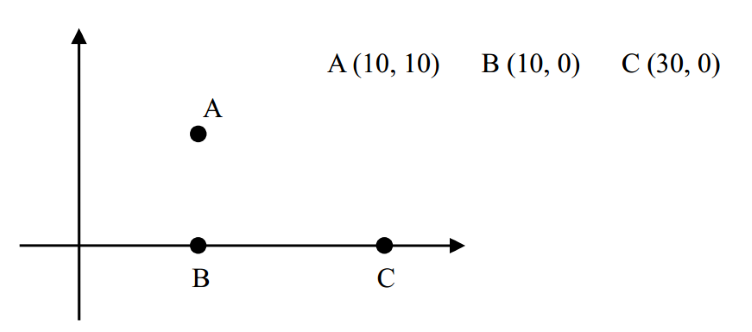
其中，$|AB|=10,|BC|=20,|AC|=10 \sqrt{5}≈22.36$。

如果没有任何卫星设备或只有 $1$ 台卫星设备 ($k=0$ 或 $k=1$)，则满足条件的最小的 $d=20$，因为 $A$ 和 $B$，$B$ 和 $C$ 可以用无线电直接通讯；而 $A$ 和 $C$ 可以用 $B$ 中转实现间接通讯 (即消息从 $A$ 传到 $B$，再从 $B$ 传到 $C$)；

如果有 $2$ 台卫星设备 ($k=2$)，则可以把这两台设备分别分配给 $B$ 和 $C$ ，这样最小的 $d$ 可取 $10$，因为 $A$ 和 $B$ 之间可以用无线电直接通讯；$B$ 和 $C$ 之间可以用卫星直接通讯；$A$ 和 $C$ 可以用 $B$ 中转实现间接通讯。

如果有 $3$ 台卫星设备，则 $A,B,C$ 两两之间都可以直接用卫星通讯，最小的 $d$ 可取 $0$。

**输入格式**
第一行为由空格隔开的两个整数 $n,k$;

接下来 $n$ 行，每行两个整数，第 $i$ 行的 $x_i,y_i$ 表示第 $i$ 座村庄的坐标 ($x_i,y_i$)。

**输出格式**
一个实数，表示最小的 $d$ 值，结果保留 $2$ 位小数。

**数据范围**

$1≤n≤500,0≤x,y≤10^4,0≤k≤100$

**输入样例**：
```cpp {.line-numbers}
3 2
10 10
10 0
30 0
```

**输出样例**：
```cpp {.line-numbers}
10.00
```

### 二、$Kruskal$算法
* 假设已经确定了参数$d$的大小, 那么所有两个 **距离$dist≤d$的村庄** 就可以建立联系, 在图中建立了若干连通块 


* **参数$d$的大小** 与 **联通块的数量** 成反比:
  * 当$d=0$, 所有村庄间通过卫星相连,共有$n$个连通块
  * 当$d>=max(dist_{i,j})$ ($dist_{i,j}$:图中村庄$i,j$之间的距离), 所有顶点连通, 共有$1$个连通块

![](https://cdn.acwing.com/media/article/image/2021/12/23/85607_c16488ef63-a.png)

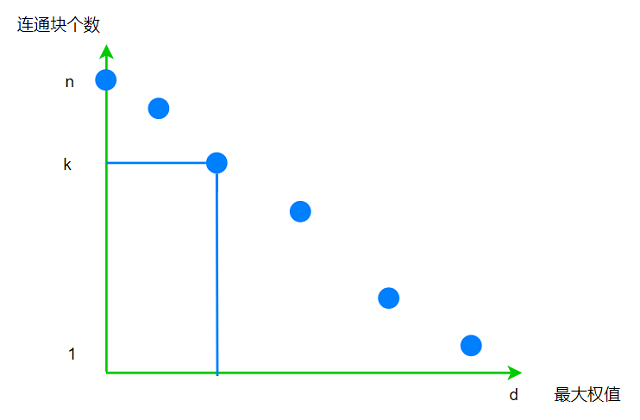
而题目的要求是:  <font color='red' size=4><b>找到满足连通块个数不超过$k$个的最小的$d$</b></font> 

本质上就是对$Kruskal$算法的 **魔改** 一下,考虑$Kruskal$的计算过程:

按照边权递增的顺序, 当把两个不连通的顶点连通时, 相当于在图中减少了一个连通块. 在连通块恰好减少到$k$时, 对应的边权因为有递增的保证, 所以是满足条件的最小边权

```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;

typedef pair<int, int> PII;
#define x first
#define y second

const int N = 510;
// 有向图 边数最多：n(n-1)/2
// 可以想象一下，每个点可以向其它n-1个点引边，共有n个点，就是n*(n-1)条边，因为一来一回算了两次，所以就是 n*(n-1)/2个，最大值设定 N*N/2
const int M = N * N / 2;
int n, k;

struct Edge {
    int a, b;
    double w;
    const bool operator<(const Edge &t) const {
        return w < t.w;
    }
} e[M];
int el;

// 每个村庄的坐标
PII q[M];

// 欧几里得距离
double get_dist(PII a, PII b) {
    int x = a.x - b.x, y = a.y - b.y;
    return sqrt(x * x + y * y);
}

// 并查集
int p[N];
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
    cin >> n >> k;                                       // n座村庄,有k台卫星设备
    for (int i = 0; i < n; i++) cin >> q[i].x >> q[i].y; // 村庄坐标

    // 枚举所有点与点之间的边
    for (int i = 0; i < n; i++)
        for (int j = i + 1; j < n; j++)
            // 记录单向边即可
            e[el++] = {i, j, get_dist(q[i], q[j])};

    // 边权由小到大排序
    sort(e, e + el);

    // 并查集初始化
    for (int i = 0; i < n; i++) p[i] = i;

    int cnt = n; // 剩余的连通块数量
    double res = 0;

    // 原则：长的用卫星,短的用无线电收发机
    // 合并完之后，正好剩下k个连通块,停止，每个连通块上安装卫星即可全面通讯

    // 给原图的节点中n - k个节点生成一棵最小生成树
    for (int i = 0; i < el; i++) { // 枚举每条边
        if (cnt == k) break;       // 剩余点数为k时停止, 在这k个点上建立卫星站
        int a = find(e[i].a), b = find(e[i].b);
        if (a != b) {
            p[a] = b;
            cnt--;        // 连通块数量-1
            res = e[i].w; // 不停的记录参数d的上限
        }
    }
    printf("%.2lf\n", res);
    return 0;
}
```