##[$AcWing$ $831$. $KMP$字符串](https://www.acwing.com/problem/content/833/)
**[参考博文:从头到尾彻底理解$KMP$](https://blog.csdn.net/v_JULY_v/article/details/7041827)**
### 一、题目描述
给定一个字符串 $S$,以及一个模式串 $P$,所有字符串中只包含大小写英文字母以及阿拉伯数字。
模式串 $P$ 在字符串 $S$ 中多次作为子串出现。
求出模式串 $P$ 在字符串 $S$ 中所有出现的位置的起始下标。
**输入格式**
第一行输入整数 $N$,表示字符串 $P$ 的长度。
第二行输入字符串 $P$。
第三行输入整数 $M$,表示字符串 $S$ 的长度。
第四行输入字符串 $S$。
**输出格式**
共一行,输出所有出现位置的起始下标(下标从 $0$ 开始计数),整数之间用空格隔开。
**数据范围**
$1≤N≤10^5$
$1≤M≤10^6$
**输入样例:**
```cpp {.line-numbers}
3
aba
5
ababa
```
**输出样例:**
```cpp {.line-numbers}
0 2
```
### 二、暴力解法
解决子串匹配的暴力算法很容易,子串的首部和字符串的第 $i$ 个对齐,开始匹配,直到匹配成功或者匹配失败;如果匹配失败,则子串的首部需要和字符串的第 $i+1$ 个对齐,并重新开始匹配:
**动画展示**
 **实现代码**
```cpp {.line-numbers}
#include
using namespace std;
int find(string p, string s) {
int n = s.size(), i = 0;
int m = p.size(), j = 0;
for (i = 0; i <= n - m; i++) {
for (j = 0; j < m; j++)
if (p[j] != s[i + j]) break;
if (j == m) return i;
}
return -1;
}
int main() {
string txt = "aaacaaab", pat = "aaab";
cout << find(pat, txt) << endl;
// 答案:4
// 表示从索引号为4开始存在第一个匹配
return 0;
}
```
### 三、 $KMP$ 算法
$KMP$ 算法,通常用于在一个 **文本字符串$S$** 中查找一个 **匹配串**$P$ 的 **出现位置** 和 **出现次数**。
#### 动画展示
**实现代码**
```cpp {.line-numbers}
#include
using namespace std;
int find(string p, string s) {
int n = s.size(), i = 0;
int m = p.size(), j = 0;
for (i = 0; i <= n - m; i++) {
for (j = 0; j < m; j++)
if (p[j] != s[i + j]) break;
if (j == m) return i;
}
return -1;
}
int main() {
string txt = "aaacaaab", pat = "aaab";
cout << find(pat, txt) << endl;
// 答案:4
// 表示从索引号为4开始存在第一个匹配
return 0;
}
```
### 三、 $KMP$ 算法
$KMP$ 算法,通常用于在一个 **文本字符串$S$** 中查找一个 **匹配串**$P$ 的 **出现位置** 和 **出现次数**。
#### 动画展示
 #### 步骤说明
- **步骤一**
判断此时的$i,j$是否超出各自字符串的限制:
- 若$j$超出$P$的限制则退出并返回匹配成功处的位置下标,**表示完成了子串的完整匹配**
- 若$i$超出$S$的限制,**则退出并说明无解**
- 比较$S[i]$,$P[j]$:
- 若$S[i]==P[j]$或者$j==−1$,则$i + + , j + +$,重复步骤一
- 若$S[i]\neq P[j]$,进入步骤二
- **步骤二**
失配时,$i$不变,$j=ne[j]$,进入步骤一
#### $Q:ne$数组是怎么生成的?
假设一个 **模式串** 长度为$n$,则存在$n$个前缀与$n$个后缀,舍去其中长度为$n$的情况,则剩下$n − 1$个前缀与$n−1$个后缀,**前缀与后缀的最大匹配就是该字符串的最长公共前缀后缀长度**, $ne[i]$代表的就是前$i$个字符组成的子串中,最长公共前后缀的长度
由上可知,$ne$的最小值就是$0$(不包括第一个位置哨兵位置的$−1$)
比如说当前字符串为$A B C D A B$
则有:
#### 步骤说明
- **步骤一**
判断此时的$i,j$是否超出各自字符串的限制:
- 若$j$超出$P$的限制则退出并返回匹配成功处的位置下标,**表示完成了子串的完整匹配**
- 若$i$超出$S$的限制,**则退出并说明无解**
- 比较$S[i]$,$P[j]$:
- 若$S[i]==P[j]$或者$j==−1$,则$i + + , j + +$,重复步骤一
- 若$S[i]\neq P[j]$,进入步骤二
- **步骤二**
失配时,$i$不变,$j=ne[j]$,进入步骤一
#### $Q:ne$数组是怎么生成的?
假设一个 **模式串** 长度为$n$,则存在$n$个前缀与$n$个后缀,舍去其中长度为$n$的情况,则剩下$n − 1$个前缀与$n−1$个后缀,**前缀与后缀的最大匹配就是该字符串的最长公共前缀后缀长度**, $ne[i]$代表的就是前$i$个字符组成的子串中,最长公共前后缀的长度
由上可知,$ne$的最小值就是$0$(不包括第一个位置哨兵位置的$−1$)
比如说当前字符串为$A B C D A B$
则有:
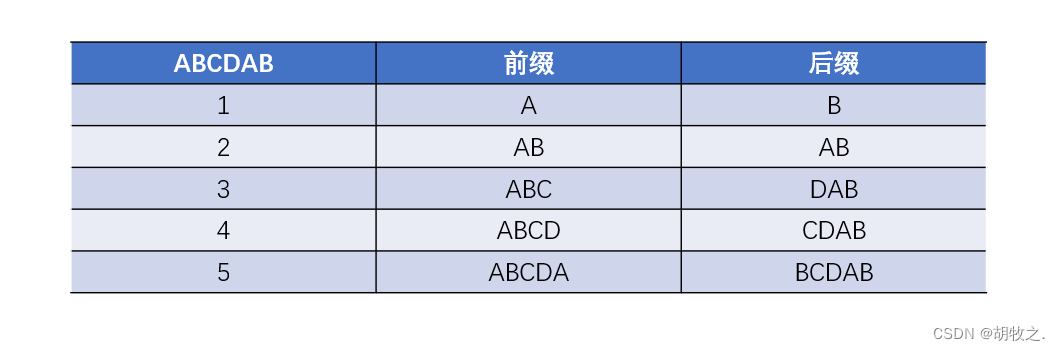 **当失配时,$j=ne[j]$,充分利用已知信息,找出模式串中最值得再次匹配的位置**
**求$ne$数组和$kmp$很相似,相当于自己找自己的匹配串$ne[1] = 0$;下标从$2$开始,紧扣定义。**
### 四、C++ 代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 100010; // 模板串最大长度限制
const int M = 1000010; // 模式串最大长度限制
int n; // 短串长度
int m; // 长串长度
int ne[N]; // next数组
char s[M]; // 长串
char p[N]; // 短串
int main() {
cin >> n >> (p + 1) >> m >> (s + 1);
// 一、求ne数组
// i:当前试图进行匹配的S串字符,j+1是模板串当前试图与S串i位置进行匹配的字符
// j:表示已匹配的长度,一直都在尝试让j+1位和i位进行匹配,退无可退,无需再退。
// i:是从2开始的,因为ne[1]=0,表示第1个不匹配,只能重头开始,不用算
for (int i = 2, j = 0; i <= n; i++) {
while (j && p[i] != p[j + 1]) j = ne[j];
// 如果是匹配情况发生了,那么j移动到下一个位置
if (p[i] == p[j + 1]) j++;
// 记录j到ne数组中
ne[i] = j;
}
// 二、匹配字符串
// i:当前试图进行对比的S串位置
// j:最后一个已完成匹配的P串位置,那么,当前试图与S串当前位置i进行尝试对比匹配的位置是j+1
for (int i = 1, j = 0; i <= m; i++) {
while (j && s[i] != p[j + 1]) j = ne[j]; // 不行就退吧,当j==0时,表示退无可退,无需再退
// 如果是匹配情况发生了,那么j移动到下一个位置
if (s[i] == p[j + 1]) j++; // 匹配则指针前行,i不用++,因为它在自己的for循环中,自带++
if (j == n) { // 如果匹配到最大长度,说明完成了所有位置匹配
printf("%d ", i - n); // 输出开始匹配位置
j = ne[j]; // 回退,尝试继续进行匹配,看看还有没有其它可以匹配的位置
}
}
return 0;
}
```
### 五、参考资料
**[代码随想录的理论篇](https://www.bilibili.com/video/BV1PD4y1o7nd)**
**[代码随想录的代码篇](https://www.bilibili.com/video/BV1M5411j7Xx)**
[$KMP$算法](https://haokan.baidu.com/v?pd=wisenatural&vid=16960471433379543511)
[$KMP2$](https://haokan.baidu.com/v?pd=wisenatural&vid=12023963535622364019)
**当失配时,$j=ne[j]$,充分利用已知信息,找出模式串中最值得再次匹配的位置**
**求$ne$数组和$kmp$很相似,相当于自己找自己的匹配串$ne[1] = 0$;下标从$2$开始,紧扣定义。**
### 四、C++ 代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 100010; // 模板串最大长度限制
const int M = 1000010; // 模式串最大长度限制
int n; // 短串长度
int m; // 长串长度
int ne[N]; // next数组
char s[M]; // 长串
char p[N]; // 短串
int main() {
cin >> n >> (p + 1) >> m >> (s + 1);
// 一、求ne数组
// i:当前试图进行匹配的S串字符,j+1是模板串当前试图与S串i位置进行匹配的字符
// j:表示已匹配的长度,一直都在尝试让j+1位和i位进行匹配,退无可退,无需再退。
// i:是从2开始的,因为ne[1]=0,表示第1个不匹配,只能重头开始,不用算
for (int i = 2, j = 0; i <= n; i++) {
while (j && p[i] != p[j + 1]) j = ne[j];
// 如果是匹配情况发生了,那么j移动到下一个位置
if (p[i] == p[j + 1]) j++;
// 记录j到ne数组中
ne[i] = j;
}
// 二、匹配字符串
// i:当前试图进行对比的S串位置
// j:最后一个已完成匹配的P串位置,那么,当前试图与S串当前位置i进行尝试对比匹配的位置是j+1
for (int i = 1, j = 0; i <= m; i++) {
while (j && s[i] != p[j + 1]) j = ne[j]; // 不行就退吧,当j==0时,表示退无可退,无需再退
// 如果是匹配情况发生了,那么j移动到下一个位置
if (s[i] == p[j + 1]) j++; // 匹配则指针前行,i不用++,因为它在自己的for循环中,自带++
if (j == n) { // 如果匹配到最大长度,说明完成了所有位置匹配
printf("%d ", i - n); // 输出开始匹配位置
j = ne[j]; // 回退,尝试继续进行匹配,看看还有没有其它可以匹配的位置
}
}
return 0;
}
```
### 五、参考资料
**[代码随想录的理论篇](https://www.bilibili.com/video/BV1PD4y1o7nd)**
**[代码随想录的代码篇](https://www.bilibili.com/video/BV1M5411j7Xx)**
[$KMP$算法](https://haokan.baidu.com/v?pd=wisenatural&vid=16960471433379543511)
[$KMP2$](https://haokan.baidu.com/v?pd=wisenatural&vid=12023963535622364019)


