##[$AcWing$ $836$. 合并集合](https://www.acwing.com/problem/content/838/)

### 一、题目描述
一共有 $n$ 个数，编号是 $1∼n$，最开始每个数各自在一个集合中。

现在要进行 $m$ 个操作，操作共有两种：

`M a b`，将编号为 $a$ 和 $b$ 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
`Q a b`，询问编号为 $a$ 和 $b$ 的两个数是否在同一个集合中；

**输入格式**
第一行输入整数 $n$ 和 $m$。

接下来 $m$ 行，每行包含一个操作指令，指令为 `M a b` 或 `Q a b` 中的一种。

**输出格式**
对于每个询问指令 `Q a b`，都要输出一个结果，如果 `a` 和 `b` 在同一集合内，则输出 `Yes`，否则输出 `No`。

每个结果占一行。

**数据范围**
$1≤n,m≤10^5$

**输入样例：**
```cpp {.line-numbers}
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
```

**输出样例：**
```cpp {.line-numbers}
Yes
No
Yes
```

### 二、题目解析
<center><img src='https://cdn.acwing.com/media/article/image/2021/02/03/64630_7ab0776065-并查集的递归理解.png'></center>

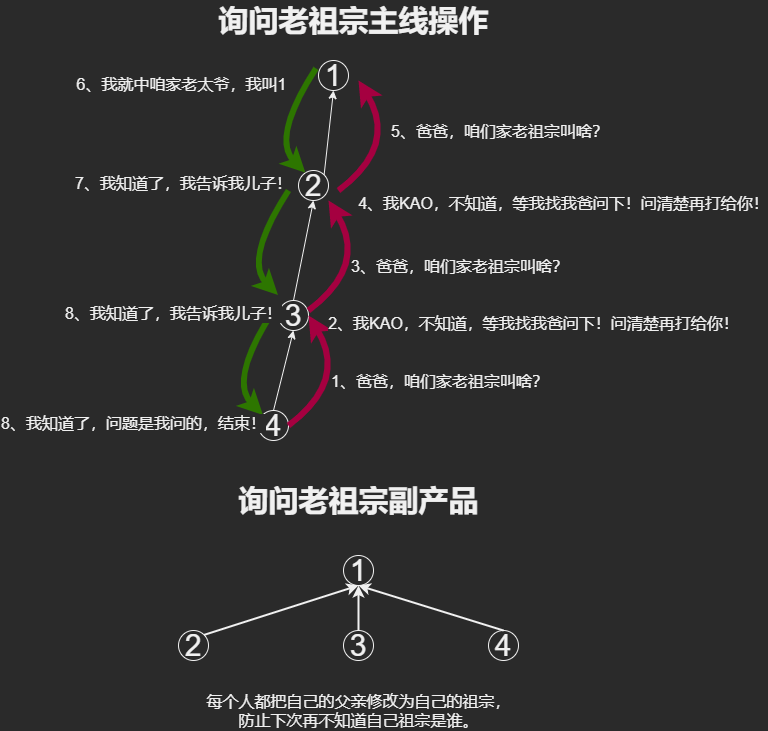**最裸并查集**
1、将两个集合合并。

2、询问两个元素是否在一个集合当中 ，近乎$O(1)$时间内支持两个操作

基本原理：每个集合用一棵树来表示，树根的编号就是整个集合的编号，每个节点存储它的父节点，$p[x]$表示$x$的父节点

* 如何判断树根？
`if(p[x]==x)`

* 如何求$x$的集合编号？
`find(x)`

* 如何合并两个集合?
`p[find(a)] = find(b)`

### 三、实现代码
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int N = 100010;

int n, m;
int p[N];

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]); // 路径压缩
    return p[x];
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) p[i] = i; // 自己是自己的祖先

    while (m--) {
        char op;
        int a, b;
        cin >> op >> a >> b;
        if (op == 'M')
            p[find(a)] = find(b); // a家族加入b家族
        else {
            if (find(a) == find(b))
                puts("Yes");
            else
                puts("No");
        }
    }
    return 0;
}
```