##[$AcWing$ $843$. $n$-皇后问题](https://www.acwing.com/problem/content/description/845/)
### 一、题目描述
$n$−皇后问题是指将 $n$ 个皇后放在 $n×n$ 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。
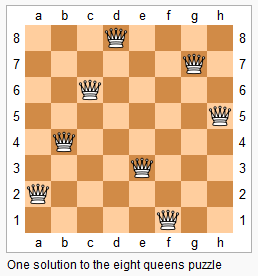 现在给定整数 $n$,请你输出所有的满足条件的棋子摆法。
**输入格式**
共一行,包含整数 $n$。
**输出格式**
每个解决方案占 $n$ 行,每行输出一个长度为 $n$ 的字符串,用来表示完整的棋盘状态。
其中 $.$ 表示某一个位置的方格状态为空,$Q$ 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
**数据范围**
$1≤n≤9$
**输入样例:**
```cpp {.line-numbers}
4
```
**输出样例:**
```cpp {.line-numbers}
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
```
### 二、题目分析
现在给定整数 $n$,请你输出所有的满足条件的棋子摆法。
**输入格式**
共一行,包含整数 $n$。
**输出格式**
每个解决方案占 $n$ 行,每行输出一个长度为 $n$ 的字符串,用来表示完整的棋盘状态。
其中 $.$ 表示某一个位置的方格状态为空,$Q$ 表示某一个位置的方格上摆着皇后。
每个方案输出完成后,输出一个空行。
注意:行末不能有多余空格。
输出方案的顺序任意,只要不重复且没有遗漏即可。
**数据范围**
$1≤n≤9$
**输入样例:**
```cpp {.line-numbers}
4
```
**输出样例:**
```cpp {.line-numbers}
.Q..
...Q
Q...
..Q.
..Q.
Q...
...Q
.Q..
```
### 二、题目分析
 ### 三、实现代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1e5 + 10; // Q:为什么这里是110,还是最大是9吗?这是因为在下面的数组使用中,采用了+8的偏移策略,需要大一点,只要开不死,就往死里开!
int path[N];
int n;
int b1[N], b2[N], b3[N];
void dfs(int u) {
if (u == n + 1) { // 全部行都摆上皇后
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (j == path[i])
printf("Q");
else
printf(".");
}
puts("");
}
puts("");
return;
}
for (int i = 1; i <= n; i++) { // x行y列
/*
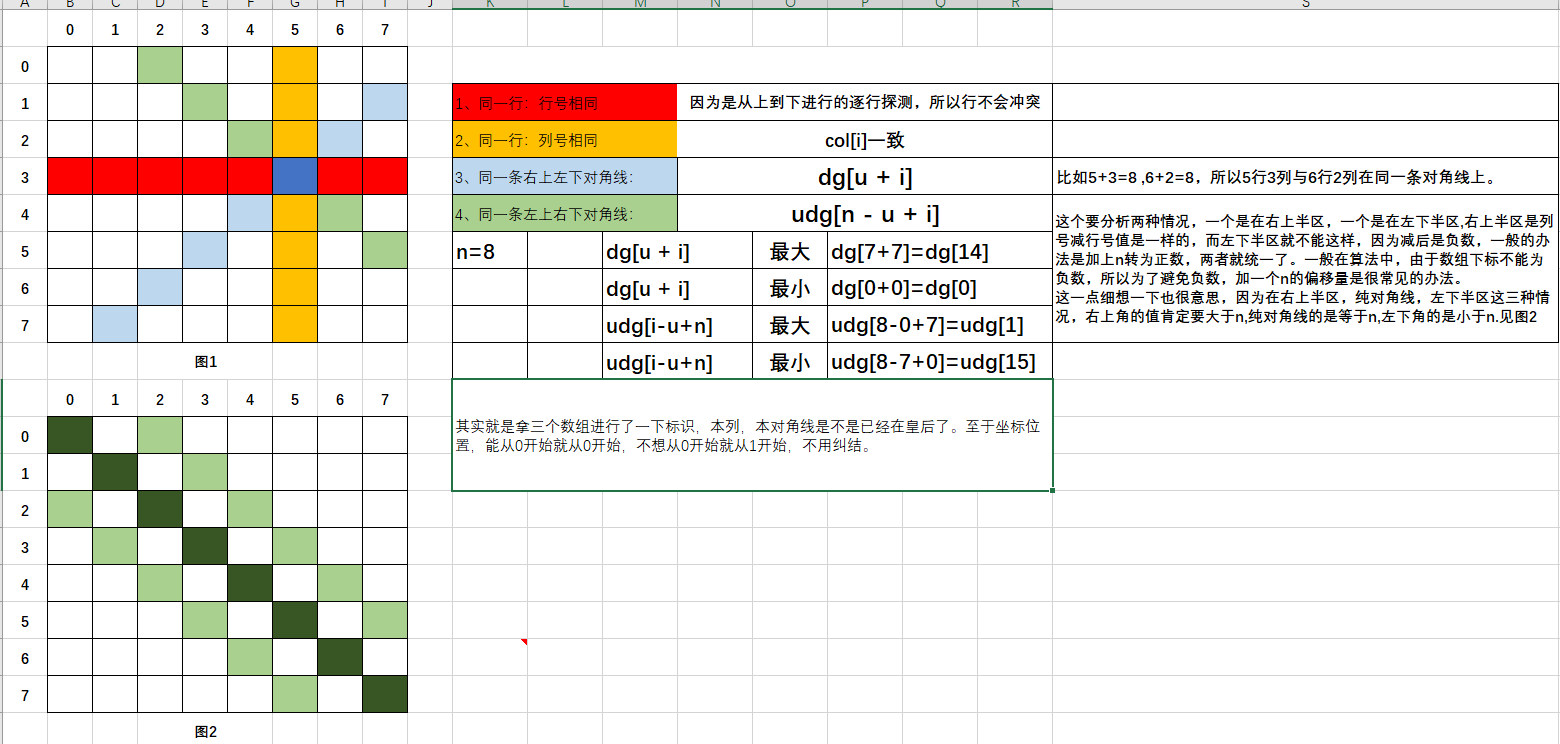
1、因为x上按行一行一行来的,所以不用考虑行的冲突,只需要考虑列、正对角线,反对角线三个方向。
2、b2[x+i] 因为同一正角线的位置,行+列是相等的,如果我们设置了 行+列使用过了,
那么,其它再检查到同一对角线时,就会发现行+列已使用过
3、b3[x - i + 8] 因为同一反对角线的位置,行-列是相等的,但可能行>列,也可能列>行,
这要看它是最长对角线的右上方还是左下方,右上方x>y,左下方x> n;
dfs(1);
return 0;
}
```
### 三、实现代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1e5 + 10; // Q:为什么这里是110,还是最大是9吗?这是因为在下面的数组使用中,采用了+8的偏移策略,需要大一点,只要开不死,就往死里开!
int path[N];
int n;
int b1[N], b2[N], b3[N];
void dfs(int u) {
if (u == n + 1) { // 全部行都摆上皇后
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (j == path[i])
printf("Q");
else
printf(".");
}
puts("");
}
puts("");
return;
}
for (int i = 1; i <= n; i++) { // x行y列
/*
1、因为x上按行一行一行来的,所以不用考虑行的冲突,只需要考虑列、正对角线,反对角线三个方向。
2、b2[x+i] 因为同一正角线的位置,行+列是相等的,如果我们设置了 行+列使用过了,
那么,其它再检查到同一对角线时,就会发现行+列已使用过
3、b3[x - i + 8] 因为同一反对角线的位置,行-列是相等的,但可能行>列,也可能列>行,
这要看它是最长对角线的右上方还是左下方,右上方x>y,左下方x> n;
dfs(1);
return 0;
}
```

 ### 三、实现代码
```cpp {.line-numbers}
#include
### 三、实现代码
```cpp {.line-numbers}
#include