##[$AcWing$ $1013$. 机器分配](https://www.acwing.com/problem/content/1015/)
### 一、题目描述
总公司拥有 $M$ 台 **相同** 的高效设备,准备分给下属的 $N$ 个分公司。
各分公司若获得这些设备,可以为国家提供一定的盈利。盈利与分配的设备数量有关。
问:如何分配这$M$台设备才能使国家得到的盈利最大?
求出最大盈利值。
**分配原则**:每个公司有权获得任意数目的设备,但总台数不超过设备数 $M$。
**输入格式**
第一行有两个数,第一个数是分公司数 $N$,第二个数是设备台数 $M$;
接下来是一个 $N×M$的矩阵,矩阵中的第 $i$ 行第 $j$ 列的整数表示第 $i$ 个公司分配 $j$ 台机器时的盈利。
**输出格式**
第一行输出最大盈利值;
接下 $N$行,每行有 $2$ 个数,即分公司编号和该分公司获得设备台数。
答案不唯一,输出任意合法方案即可。
**数据范围**
$1≤N≤10,1≤M≤15$
**输入样例**:
```cpp {.line-numbers}
3 3
30 40 50
20 30 50
20 25 30
```
**输出样例**:
```cpp {.line-numbers}
70
1 1
2 1
3 1
```
### 二、题意理解
**样例解读**:
```cpp {.line-numbers}
3 3
30 40 50
20 30 50
20 25 30
```
$3$个公司,$3$台机器,**机器都是一样的,一样的,记住,一样的**,要不题意理解不明白~
- $1$号公司
- 得到$1$台机器,$30$元
- 得到$2$台机器,$40$元
- 得到$3$台机器,$50$元
- $2$号公司
- 得到$1$台机器,$20$元
- 得到$2$台机器,$30$元
- 得到$3$台机器,$50$元
- $3$号公司
- 得到$1$台机器,$20$元
- 得到$2$台机器,$25$元
- 得到$3$台机器,$30$元
问,怎么分,使得国家的收益最大?
**答**:$1$号公司得到$1$台机器,$2$号公司得到$1$台机器,$3$号公司得到$1$台机器,就是$30+20+20=70$,此时国家利益最大。
### 三、不同$OJ$此题的差别
两者差别:
* $AcWing$:答案不唯一,输出任意合法方案即可($Special$ $Judge$)
* 洛谷: $P.S.$要求答案的字典序最小
尽管本题是多阶段决策的最小字典序最优方案,但是背包都也类似。
下面是卡最小字典序的数据:
```cpp {.line-numbers}
input
2 15
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 2
output
2
1 0
2 15
```
**解决办法**
* **$dfs$暴搜法**
$dfs$保证找到最大答案的时候就是字典序最少的,因为我从$1$号-$n$号枚举用的多少机器,用的机器数量也是由少到多。当最后得到答案相等的情况下就不用需要比较字典序了,直接$return$,只有碰到大小不一的时候才更新答案机器数。
* **$dp$+记录路径法**
* 如果使用$val > f[i][j]$转移,$f[i][j]$中记录的是第一次找到的最大值,由于输出路径是 **倒序** 输出的,所以打印出来的路径是字典序最大的。
* 如果使用$val >= f[i][j]$转移,$f[i][j]$中记录的是最后一次找到的最大值,由于输出路径是 **倒序** 输出的,所以打印出来的路径是字典序最小的。
>**$Q$:为什么加上等号就是按字典序最小输出呢?**
```cpp {.line-numbers}
for (int k = 1; k <= j; k++) {
int val = f[i - 1][j - k] + w[i][k];
if (val >= f[i][j]) {
f[i][j] = val;
path[i][j] = k;
}
}
```
**答**: 奇妙的地方是`f[i-1][j-k]`。
$k$的含义是当前分组中的物品个数,是由小到大的。而这里的计算式是$j-k$,这个东西在$k$前面的符号是负数,也就是$k$越小,值越大,$k$越大,值越小。按个循环逻辑,随着$k$的长大,就会枚举到更小的$j-k$,也就是枚举到更小的字典序。如果没有等号,就是$k$越来越大时,$j-k$越来越小,当价值一样时,越来越小的个数无法更新结果,反之,如果有等号,就是获取到字典序。
### 四、分组背包
本题乍一看很像是 **背包$DP$**,为了转换成 **背包$DP$** 问题,我们需要对里面的一些叙述做出 **等价变换**
**每家公司** 我们可以看一个 **物品组**,又因为 **所有公司** 最终能够被分配的 **机器数量** 是固定的
思路转换
① 对于分给第$i$个公司的不同机器数量可以分别看作是一个物品组内的物品数量。
② 物品$k$的含义:分给第$i$个公司$k$台机器
③ 物品$k$的体积:因为一个机器算一个,所以体积也是$k$
④ 物品$k$的价值:$w_{k}$
直接上 **分组背包** 的 **闫氏DP分析法**
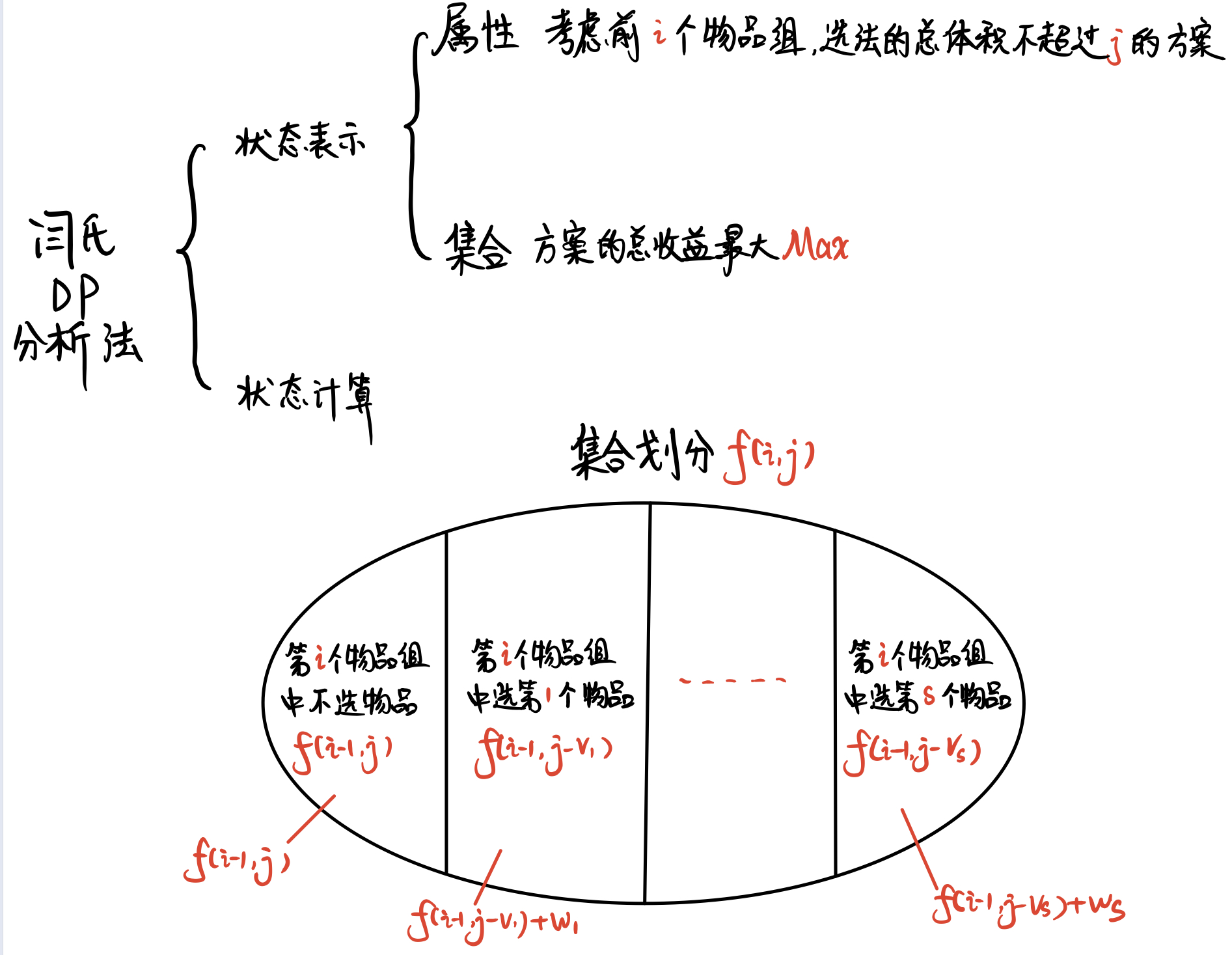 初始状态 :$f[0][0]$
目标状态 :$f[N][M]$
#### 动态规划求状态转移路径
这里我介绍一个从 **图论** 角度思考的方法
**动态规划** 本质是在一个 **拓扑图** 内找 **最短路**
我们可以把每个 **状态**$f[i][j]$看作一个 **点**,**状态的转移** 看作一条 **边**,把 **状态的值** 理解为 **最短路径长**
具体如下图所示:
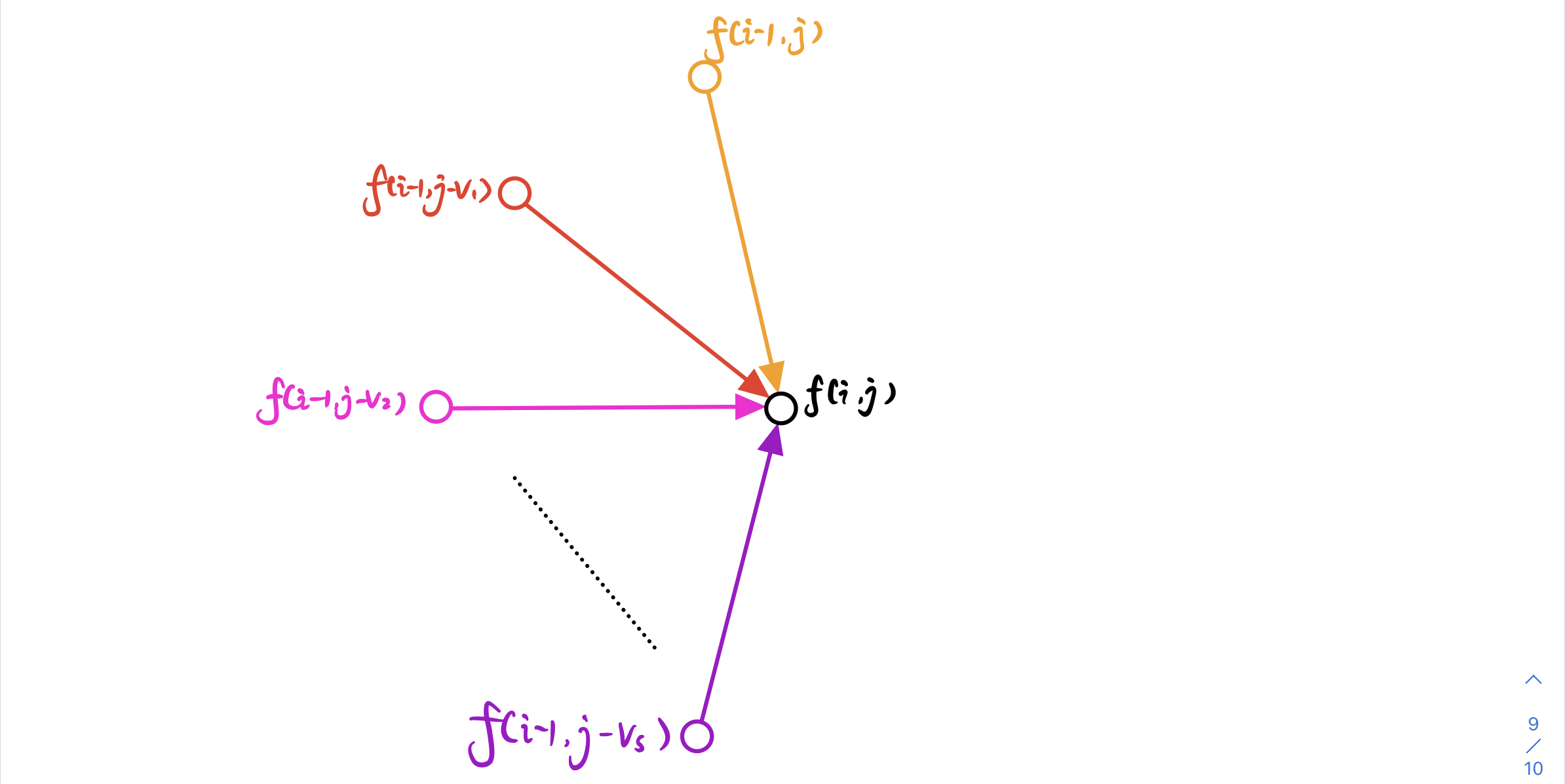
对于 **点** $f[i][j]$ 来说,他的 **最短路径长** 是通过所有到他的 **边** 更新出来的
更新 **最短路** 的 **规则** 因题而已,本题的 **更新规则** 是
$$\large f(i,j)=max(f(i−1,j−v_i))+w_i$$
最终,我们会把从 **初始状态**(起点)到 **目标状态** (终点)的 **最短路径长** 更新出来
随着这个更新的过程,也就在整个 **图** 中生成了一颗 **最短路径树**
该 **最短路径树** 上 **起点** 到 **终点** 的 **路径** 就是我们要求的 **动态规划的状态转移路径**
如下图所示:
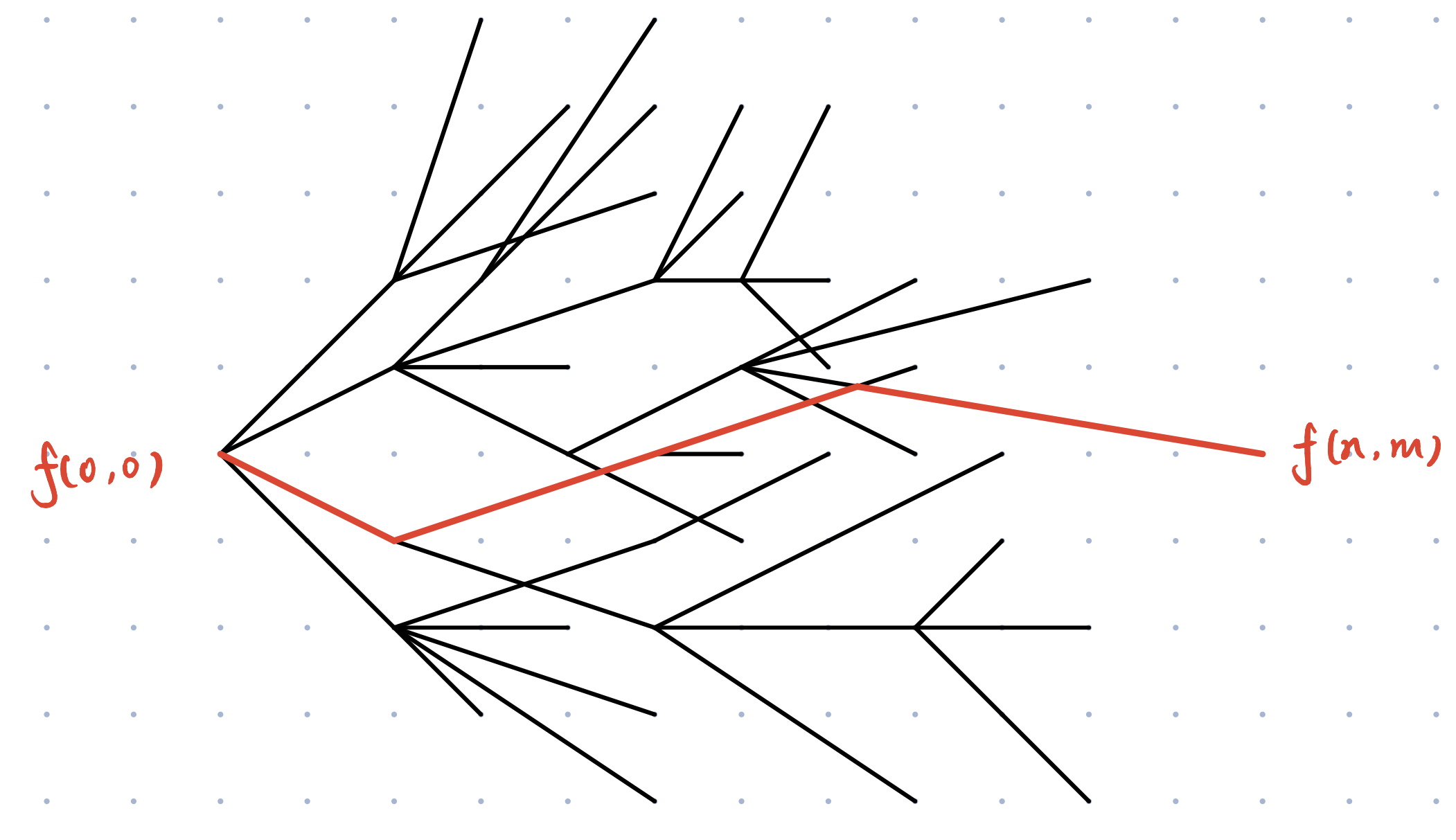
那么 **动态规划求状态转移路径** 就变成了在 **拓扑图** 中找 **最短路径** 的问题了
可以直接沿用 **最短路** 输出路径的方法就可以找出 **状态的转移**
**二维数组写法**
```cpp {.line-numbers}
#include
using namespace std;
const int N = 30;
int n, m;
int w[N][N];
int f[N][N];
int path[N][N];
//致敬墨染空大神
void out(int i, int j) {
if (i == 0) return; //走出界就完事了
int k = path[i][j];
out(i - 1, j - k); //利用递推的栈机制,后序输出,太强了~
printf("%d %d\n", i, k);
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%d", &w[i][j]);
/*1、原始版本*/
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++) {
f[i][j] = f[i - 1][j];
path[i][j] = 0;
for (int k = 1; k <= j; k++) {
int val = f[i - 1][j - k] + w[i][k];
if (val >= f[i][j]) {
f[i][j] = val;
path[i][j] = k;
}
}
}
/*2、优化一下代码*/
/*
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= j; k++) {
int val = f[i - 1][j - k] + w[i][k];
if (val >= f[i][j]) {
f[i][j] = val;
path[i][j] = k;
}
}
}*/
//输出最大值
printf("%d\n", f[n][m]);
//输出路径
out(n, m);
return 0;
}
```
**一维数组写法**
```cpp {.line-numbers}
#include
using namespace std;
const int N = 20;
int f[N];
int w[N];
int path[N][N];
//致敬墨染空大神
void out(int i, int j) {
if (i == 0) return; //走出界就完事了
int k = path[i][j];
out(i - 1, j - k); //利用递推的栈机制,后序输出,太强了~
printf("%d %d\n", i, k);
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++)
scanf("%d", &w[j]);
for (int j = m; j; j--)
for (int k = 1; k <= j; k++) {
int val = f[j - k] + w[k];
if (val >= f[j]) {
f[j] = val;
//在状态转移时,记录路径
path[i][j] = k;
}
}
}
//输出结果
printf("%d\n", f[m]);
//输出路径
out(n, m);
return 0;
}
```
**找最短路的递归写法**
```cpp {.line-numbers}
#include
using namespace std;
const int N = 20;
int n, m;
int w[N][N];
int f[N][N];
int a[N], al;
void dfs(int u, int v) {
if (u == 0) return;
// 寻找当前状态f[i][j]是从上述哪一个f[i-1][k]状态转移过来的
for (int i = 0; i <= v; i++) {
if (f[u - 1][v - i] + w[u][i] == f[u][v]) {
a[++al] = i;
dfs(u - 1, v - i);
return;
}
}
}
int main() {
// input
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> w[i][j];
// dp
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
for (int k = 0; k <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k] + w[i][k]);
cout << f[n][m] << endl;
// find path
dfs(n, m);
int id = 1;
for (int i = al; i; i--) cout << id++ << " " << a[i] << endl;
return 0;
}
```
### 四、深度优先搜索
数据范围比较小,$1<=N<=10,1<=M<=15$,把$m$个机器分配给$n$个公司,暴力遍历所有方案
记录分配方案,如果能更新最优解,顺便更新一下最优解的分配方案
```cpp {.line-numbers}
#include
using namespace std;
const int N = 11;
const int M = 16;
int n;
int m;
int path[N], res[N];
int w[N][M];
int Max;
// u:第几个公司 s:已经产生的价值 r:剩余的机器数量
void dfs(int u, int s, int r) {
if (u == n + 1) {
if (s > Max) {
Max = s;
memcpy(res, path, sizeof path);
}
return;
}
for (int i = 0; i <= r; i++) {
path[u] = i;
dfs(u + 1, s + w[u][i], r - i);//给u号公司分配i个机器
// path[u] = 0;
//按照回溯法,此处应该写path[u]还原现场,但本题中即使不还原现场,path[u]也会被下一次循环所覆盖,所以这句可以省略掉
}
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%d", &w[i][j]);
dfs(1, 0, m);
printf("%d\n", Max);
//输出最优答案时的路径
for (int i = 1; i <= n; i++) printf("%d %d\n", i, res[i]);
return 0;
}
```
初始状态 :$f[0][0]$
目标状态 :$f[N][M]$
#### 动态规划求状态转移路径
这里我介绍一个从 **图论** 角度思考的方法
**动态规划** 本质是在一个 **拓扑图** 内找 **最短路**
我们可以把每个 **状态**$f[i][j]$看作一个 **点**,**状态的转移** 看作一条 **边**,把 **状态的值** 理解为 **最短路径长**
具体如下图所示:

对于 **点** $f[i][j]$ 来说,他的 **最短路径长** 是通过所有到他的 **边** 更新出来的
更新 **最短路** 的 **规则** 因题而已,本题的 **更新规则** 是
$$\large f(i,j)=max(f(i−1,j−v_i))+w_i$$
最终,我们会把从 **初始状态**(起点)到 **目标状态** (终点)的 **最短路径长** 更新出来
随着这个更新的过程,也就在整个 **图** 中生成了一颗 **最短路径树**
该 **最短路径树** 上 **起点** 到 **终点** 的 **路径** 就是我们要求的 **动态规划的状态转移路径**
如下图所示:

那么 **动态规划求状态转移路径** 就变成了在 **拓扑图** 中找 **最短路径** 的问题了
可以直接沿用 **最短路** 输出路径的方法就可以找出 **状态的转移**
**二维数组写法**
```cpp {.line-numbers}
#include
using namespace std;
const int N = 30;
int n, m;
int w[N][N];
int f[N][N];
int path[N][N];
//致敬墨染空大神
void out(int i, int j) {
if (i == 0) return; //走出界就完事了
int k = path[i][j];
out(i - 1, j - k); //利用递推的栈机制,后序输出,太强了~
printf("%d %d\n", i, k);
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%d", &w[i][j]);
/*1、原始版本*/
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++) {
f[i][j] = f[i - 1][j];
path[i][j] = 0;
for (int k = 1; k <= j; k++) {
int val = f[i - 1][j - k] + w[i][k];
if (val >= f[i][j]) {
f[i][j] = val;
path[i][j] = k;
}
}
}
/*2、优化一下代码*/
/*
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= j; k++) {
int val = f[i - 1][j - k] + w[i][k];
if (val >= f[i][j]) {
f[i][j] = val;
path[i][j] = k;
}
}
}*/
//输出最大值
printf("%d\n", f[n][m]);
//输出路径
out(n, m);
return 0;
}
```
**一维数组写法**
```cpp {.line-numbers}
#include
using namespace std;
const int N = 20;
int f[N];
int w[N];
int path[N][N];
//致敬墨染空大神
void out(int i, int j) {
if (i == 0) return; //走出界就完事了
int k = path[i][j];
out(i - 1, j - k); //利用递推的栈机制,后序输出,太强了~
printf("%d %d\n", i, k);
}
int main() {
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++)
scanf("%d", &w[j]);
for (int j = m; j; j--)
for (int k = 1; k <= j; k++) {
int val = f[j - k] + w[k];
if (val >= f[j]) {
f[j] = val;
//在状态转移时,记录路径
path[i][j] = k;
}
}
}
//输出结果
printf("%d\n", f[m]);
//输出路径
out(n, m);
return 0;
}
```
**找最短路的递归写法**
```cpp {.line-numbers}
#include
using namespace std;
const int N = 20;
int n, m;
int w[N][N];
int f[N][N];
int a[N], al;
void dfs(int u, int v) {
if (u == 0) return;
// 寻找当前状态f[i][j]是从上述哪一个f[i-1][k]状态转移过来的
for (int i = 0; i <= v; i++) {
if (f[u - 1][v - i] + w[u][i] == f[u][v]) {
a[++al] = i;
dfs(u - 1, v - i);
return;
}
}
}
int main() {
// input
cin >> n >> m;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> w[i][j];
// dp
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
for (int k = 0; k <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k] + w[i][k]);
cout << f[n][m] << endl;
// find path
dfs(n, m);
int id = 1;
for (int i = al; i; i--) cout << id++ << " " << a[i] << endl;
return 0;
}
```
### 四、深度优先搜索
数据范围比较小,$1<=N<=10,1<=M<=15$,把$m$个机器分配给$n$个公司,暴力遍历所有方案
记录分配方案,如果能更新最优解,顺便更新一下最优解的分配方案
```cpp {.line-numbers}
#include
using namespace std;
const int N = 11;
const int M = 16;
int n;
int m;
int path[N], res[N];
int w[N][M];
int Max;
// u:第几个公司 s:已经产生的价值 r:剩余的机器数量
void dfs(int u, int s, int r) {
if (u == n + 1) {
if (s > Max) {
Max = s;
memcpy(res, path, sizeof path);
}
return;
}
for (int i = 0; i <= r; i++) {
path[u] = i;
dfs(u + 1, s + w[u][i], r - i);//给u号公司分配i个机器
// path[u] = 0;
//按照回溯法,此处应该写path[u]还原现场,但本题中即使不还原现场,path[u]也会被下一次循环所覆盖,所以这句可以省略掉
}
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%d", &w[i][j]);
dfs(1, 0, m);
printf("%d\n", Max);
//输出最优答案时的路径
for (int i = 1; i <= n; i++) printf("%d %d\n", i, res[i]);
return 0;
}
```
