##[$AcWing 1322$. 取石子游戏](https://www.acwing.com/problem/content/1324/)

### 一、题目描述
在研究过 $Nim$ 游戏及各种变种之后，$Orez$ 又发现了一种全新的取石子游戏，这个游戏是这样的：

有 $n$ 堆石子，将这 $n$ 堆石子摆成一排。

游戏由两个人进行，两人轮流操作，每次操作者都可以从 **最左** 或 **最右** 的一堆中取出若干颗石子，可以将那一堆全部取掉，但不能不取，**不能操作的人就输了**。

$Orez$ 问：对于任意给出的一个初始局面，是否存在先手必胜策略。

**输入格式**
第一行为一个整数 $T$，表示有 $T$ 组测试数据。

对于每组测试数据，第一行为一个整数 $n$，表示有 $n$ 堆石子，第二行为 $n$ 个整数 $a_i$ ，依次表示每堆石子的数目。

**输出格式**
对于每组测试数据仅输出一个整数 $0$ 或 $1$，占一行。

其中 $1$ 表示有先手必胜策略，$0$ 表示没有。

**数据范围**
$1≤T≤10,1≤n≤1000,1≤a_i≤10^9$

**输入样例**：
```cpp {.line-numbers}
1
4
3 1 9 4
```
输出样例：
```cpp {.line-numbers}
0
```

### 二、思考过程

#### 1、状态定义

① 设 $left[i][j]$ 表示在 $[i,j]$ 已经固定的区间 **左侧** 放上一堆数量为 $left[i][j]$ 的石子后，**先手必败**
② 设 $right[i][j]$ 表示在 $[i,j]$ 已经固定的区间  **右侧** 放上一堆数量为 $right[i][j]$ 的石子后，**先手必败**

即：$(left[i][j],\underbrace{a_i,a_{i+1},\cdots,a_j}_{a[i]\sim a[j]})$,$(\underbrace{a_i,a_{i+1},\cdots,a_j}_{a[i]\sim a[j]},right[i][j])$ 为 **先手必败** 局面

有如下两个性质：

#### 2、$left[i][j]$,$right[i][j]$一定存在
**反证法**:
假设不存在满足定义的 $left[i][j]$，则对于 **任意非负整数** $x$，有形如:

$$\large \underbrace{x,a_i,a_{i+1},\cdots,a_j}_{A(x)}$$ 都为 **必胜局面** ,记为 $A(x)$ 局面。

由于 $A(x)$ 为必胜局面，故从 $A(x)$ 局面 <font color='red' size=4><b>必然存在若干种办法一步可达必败局面</b></font>。

若从最左边一堆中拿，<font color='red' size=4><b>因为假设原因，不可能变成必败局面</b></font>，因为这样得到的局面仍形如 $A(x)$。


左边拿没用，只能考虑从右边拿(即从$a_j$里拿)：

于是设 $A(x)$ 一步可达的某个 **必败局面**为 $(x,a_i,a_{i+1},\cdots,a_{j-1},y)$，显然有 $0 \le y < a_j$。

**由于 $x$ 有无限个，但 $y$ 只有 $a_j$种——根据抽屉原理，必然存在 $x_1,x_2(x_1 > x_2),y$ 满足 $(x_1,a_i,a_{i+1},\cdots,a_{j-1},y)$ 和 $(x_2,a_i,a_{i+1},\cdots,a_{j-1},y)$ 都是必败局面**。但这两个必败局面之间 **实际一步可达**(比如拿走$x_1-x_2$个)，矛盾，假设不成立，原命题成立。

#### 3、$left[i][j]$,$right[i][j]$必然唯一

**反证法**:
假设 $left(i,j)$ 不唯一，则存在非负整数 $x_1,x_2(x_1 \neq x_2)$，使得$(x_1,a_i,a_{i+1},⋯,a_{j−1},a_j)$ 和 $(x_2,a_i,a_{i+1},\cdots,a_{j-1},a_j)$ 均为必败局面,而 **第一个必败局面** 可以通过拿走左侧$x_1-x_2$个石子到达另一个 **必败局面** ，矛盾，假设不成立，原命题成立。

#### 4、推论
有了上面推的$left[i][j]$唯一性，得出一个有用的推论：
**对于任意非负整数 $x \neq left(i,j)$，$\large (x,a_i,a_{i+1},\cdots,a_j)$为必胜局面**

#### 5、疑问

<font color='red' size=4><b>博弈论的题目都是可以通过动态规划来递推的</b></font>。

**$Q$:为什么定义先手必败，而不是定义先手必胜呢？**
答：因为上面证明过定义 **先手必败** 的动态规划结果数组，是肯定存在并且是唯一的.存在且唯一的，可以递推出来，如果定义的是 **先手必胜**,根据博弈论的知识，我们知道，必胜的策略不唯一，不方便递推。而如果我们采用的是 **先手必败** 这样的定义，那么由于它的存在性和唯一性，所以，只要不是它就是必胜局面！

**$Q$:怎么递推？**
递推嘛，就是类似于 **数学归纳法**,先求出初始状态是多少，然后假设$i \sim j-1$这段已经计算出$left[i][j-1],right[i][j-1]$了，现在想依赖于这两个数值推导出$left[i][j],right[i][j]$,怕写的太长麻烦，就定义了$L=left[i][j-1],R=right[i][j-1]$

![](http://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/2023/02/cccc1a0f80d1475adcf8096aa9e35ff0.png)


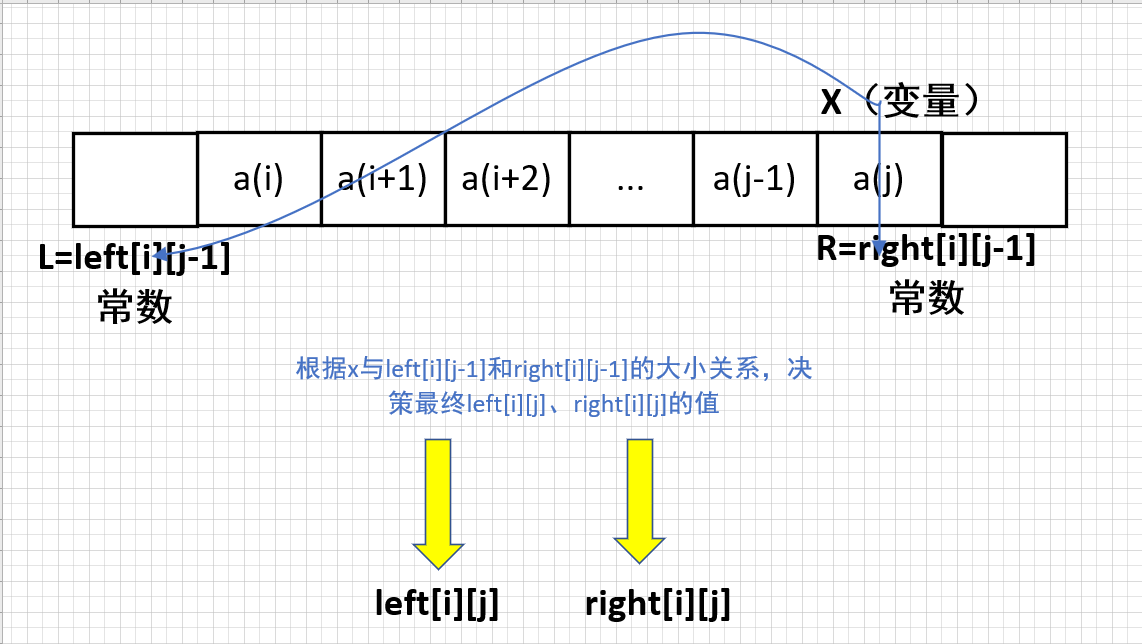
考虑三个问题：
- ① 初始值
- ② 答案在哪
- ③ 递推式
> **注：答案在哪，并不是和递推式相关，而是和状态表示相关，一定要注意**



**① 初始值**
$\large left[i][i]=right[i][i]=a_i$

当只有一堆石子时($only$ $i$)，我在这堆前面添加一堆，个数和这堆一样多，对于**两堆相同的石子**，**后手进行和先手对称的操作**,你咋干我就咋干，我拿完，你瞪眼~, **先手必败**


**② 答案在哪**
**先手必败**  $\Leftrightarrow \  left[2][n]==a[1]$ , **先手必胜**  $\Leftrightarrow \  left[2][n]!=a[1]$ 
> **解释**：$a[2] \sim a[n]$,前面放上了一个$a[1]$,
> 根据定义$left[2][n]$代表在$a[2]\sim a[n]$之前放上一个数，可以使得放后的局面必败。
> 现在放上去的是$a[1]$,可以它偏偏等于$left[2][n]$这个令人讨厌的数字,面对这样的局面，天生是死局，先手必败。



**③ 递推式**
* 变化方法：从左侧拿走一些石子或者从右侧拿走一些石子,我们需要考虑在一个局面确定后，在此局面上左侧、右侧添加一个什么数字（石子个数），才能使得变化后的局面必败。
  
* $left[i][j-1]$和$right[i][j-1]$表示$left[i][j]$和$right[i][j]$,形成$DP$递推关系


递推式需要分类讨论

先把 **特殊情况** 说清楚：

**$\large L=R=0$**

若 $R=0$ 则 $L=0$
> <font color='red'><b>注：因$R=0$,表示在[$i$,$j-1$]确定后，右侧为$0$就能满足[$i$,$j-1$]这一段为先手必败,此时，左侧增加那堆个数为$0$就可以继续保持原来的先手必败，即$L=0$,而且已经证明了$L=R=0$是唯一的。</b></font>

此时 $X>\max\{L,R\}$，也就是说 $L=0$ 和 $R=0$ 都属于 $Case$ $5$，故其它 $Case$ 满足 $L,R>0$。

令 $\displaystyle \large X=a[j](X>0)$

下面，我们按$X$与$R$的大小关系，划分为三种情况，分别进行讨论：
$$
\large \left\{\begin{matrix}
X=R & \\ 
X<R & \left\{\begin{matrix} X<L \\X \geq L \end{matrix}\right. \\
X>R & \left\{\begin{matrix} X \leq L \\X>L \end{matrix}\right. 
\end{matrix}\right.
$$

* $X=R$（$Case$ $1$）
  根据 $R=right[i][j-1]$ 的定义，$X=R$则区间 $[i,j]$ 是必败局面，因此左边啥也不能添，添了反而错 
  $$\large left[i][j]=0$$

* $X<R$  
  * ① $X<L$，即 $X< \min\{L,R\}$（$Case$ $2$）
    * **必胜策略**：
    当右侧石子个数为$X$时，$\large left[i][j]=X$.即在右侧石子个数确定为$X$后，如果在左侧添加一堆石子，个数为$X$，就可以保证当前局面先手必败。
    * **证明**：
      即  **求证** $\large (X,a_i,a_{i+1},\cdots,a_{j-1},X)$为必败局面,其中$X< \min\{L,R\}$

      由于最左边和最右边的两堆石子数量相同，后手可进行和先手 **对称** 操作，当先手把某一侧的石子拿完后，后手必将获得一个形如$(y,a_i,a_{i+1},⋯,a_{j−1})$ 或 $(a_i,a_{i+1},\cdots,a_{j-1},y)$ 的局面,其中: $0<y < X<\min\{L,R\}$

      **只有左侧为$L=left(i,j-1)$这个唯一值时，才是必败态，现在不是$L$，而是$y<min(L,R)$，所以后手必胜,即先手必败**。

  <br>  

  * ② $X \geq L$，即 $L \leq X < R$（$Case$ $3$）
    * **必胜策略**：
    当右侧石子个数为$X$时，$\large left[i][j]=X+1$.即在右侧石子个数确定为$X$后，如果在左侧添加一堆石子，个数为$X+1$，就可以保证当前局面先手必败。
    * **证明**：
      即 **求证** $(X+1,a_i,a_{i+1},\cdots,a_{j-1},X)$为 **必败局面** ,其中 $L \leq X <R$

      * 若先手拿最左边一堆，设拿了以后 **还剩 $z$ 个石子**
        * 若 $z>L$，则后手将最右堆拿成 $z-1$ 个石子（$z-1 \ge L>0$），**保证左侧比右侧多$1$个石子**,就能回到 $Case$ $3$ 本身，递归证明即可
        * 若 $z=L$，则后手将最右堆拿完，根据 $L=left[i][j-1]$ 定义知此时局面必败
        * 若 $0<z<L$，则后手将最右堆拿成 $z$ 个石子，**由 $Case$ $2$ 知此时是必败局面**
        * 若 $z=0$，此时最右堆石子数 $X$ 满足 $L \le X<R$，结合 $right[i][j-1]$ 定义知 **此局面后手必胜,也就是先手必败**
      <br>
      * 若先手拿最右边一堆，设拿了以后 **还剩 $z$ 个石子**
        * 若 $z \ge L$，则后手将最左堆拿成 $z+1$个石子，就能回到 $Case$ $3$ 本身，递归证明即可
        * 若 $0<z<L$，则后手将最左堆拿成 $z$ 个石子，**由 $Case$ $2$ 知此时是必败局面**
        * 若 $z=0$，则后手将最左堆拿成 $L$ 个石子，由 $left[i][j-1]$定义知此时局面先手必败

* $X>R$
  * ① $X≤L$，即 $R < X \leq L$（$Case$ $4$）
    * **必胜策略**：$$\large left[i][j]=X-1$$
    * **证明**：
      * 若先手拿最左边一堆，设拿了以后还剩 $z$ 个石子。
        * 若 $z \geq R$，则后手将最右堆拿成 $z+1$ 个石子，<b>保证左侧比右侧少$1$个石子</b>,就能回到 $Case$ $4$ 本身，递归证明即可。
        * 若 $0<z<R$，则后手将最右堆拿成 $z$ 个石子，由 $Case$ $2$ 知此时是必败局面。
        * 若 $z=0$，则后手将最右堆拿成 $R$ 个石子（注意 $Case$ $4$ 保证了此时最右堆石子个数 $>R$），由 $right[i][j-1])$ 的定义知此时是必败局面。
      
      <br>

      *  若先手拿最右边一堆，设拿了以后还剩 $z$ 个石子。
         * 若 $z>R$，则后手将最左边一堆拿成 $z-1$ 个石子（注意 $z-1 \ge R >0$），递归证明即可。<b>保证右侧比左侧多$1$个石子。</b>
         * 若 $z=R$，则后手把最左堆拿完，根据 $right[i][j-1]$的定义可知得到了必败局面。
         * 若 $0<z<R$，则后手将最左堆拿成 $z$ 个石子，由 $Case$ $2$ 知此时是必败局面。
         * 若 $z=0$，此时最左堆石子数量 $k$ 满足 $0<k<L$，结合 $left[i][j-1]$ 定义知局面必胜
  <br>

  * ② $X>L$，即 $X>\max\{L,R\}$（$Case$ $5$）
    * **必胜策略**：$$\large left[i][j]=x$$
    * **证明**：
       设先手将其中一堆拿成了 $z$ 个石子。
         * 若 $z>\max\{L,R\}$，后手将另一堆也拿成$z$个，回到 $Case$ $5$，递归证明。
         * 若 $0<z<\min\{L,R\}$，后手把另一堆也拿成 $z$ 个石子即可转 $Case$ $2$。
         * 若 $z=0$，将另一堆拿成 $L$ 或 $R$ 个石子即可得到必败局面。

         * 剩余的情况是 $L \le z \le R$或 $R \le z \le L$。
      ​   $Case$ $3$ 可以解决最左堆 $L +1 \le z \le R$，最右堆 $L \le z \le R-1$ 的情况
​         $Case$ $4$ 可以解决最左堆 $R \le z \le L-1$，最右堆 $R+1 \le z \le L$的情
况。
        
        ​所以只需解决最左堆 $z=L$ 和最右堆 $z=R$ 的情况。而这两种情况直接把另一堆拿完就可以得到必败局面。  



**综上所述：**
$$ \large
left[i][j]=
\large \left\{\begin{matrix}
 0 & X=R \\
 X+1&L \leq X < R  \\
X-1 & R<X \leq L \\
X & otherwise
\end{matrix}\right.
$$

> <font color='blue' size=4><b>温馨提示：</b></font>**请看清楚 $L$ 取不取等，乱取等是错的！**

同理可求 $right(i,j)$。

### 六、实现代码
```cpp {.line-numbers}
#include <cstdio>

using namespace std;
const int N = 1010;
int n;
int a[N];
int left[N][N], right[N][N]; // left,right 在 iostream库中用过了，不能用！

int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        scanf("%d", &n);
        for (int i = 1; i <= n; i++) scanf("%d", &a[i]);

        for (int len = 1; len <= n; len++)           // 枚举长度
            for (int i = 1; i + len - 1 <= n; i++) { // left[i][j],从i到j
                int j = i + len - 1;
                if (len == 1)
                    left[i][j] = right[i][j] = a[i]; // DP初始值
                else {
                    int L = left[i][j - 1], R = right[i][j - 1], X = a[j];
                    if (R == X)
                        left[i][j] = 0;
                    else if (X < L && X < R || X > L && X > R)
                        left[i][j] = X;
                    else if (L > R)
                        left[i][j] = X - 1;
                    else
                        left[i][j] = X + 1;

                    L = left[i + 1][j], R = right[i + 1][j], X = a[i];
                    if (L == X)
                        right[i][j] = 0;
                    else if (X < L && X < R || X > L && X > R)
                        right[i][j] = X;
                    else if (R > L)
                        right[i][j] = X - 1;
                    else
                        right[i][j] = X + 1;
                }
            }

        if (n == 1)
            puts("1");
        else
            printf("%d\n", left[2][n] != a[1]);
    }

    return 0;
}

```