## [$AcWing$ $342$ 道路与航线](https://www.acwing.com/problem/content/description/344/)
### 一、题目描述
农夫约翰正在一个新的销售区域对他的牛奶销售方案进行调查。
他想把牛奶送到 $T$ 个城镇，编号为 $1$∼$T$。
这些城镇之间通过 $R$ 条道路 (编号为 $1$ 到 $R$) 和 $P$ 条航线 (编号为 $1$ 到 $P$) 连接。
每条道路 $i$ 或者 航线 $i$ 连接城镇 $A_i$ 到 $B_i$，花费为 $C_i$。
对于道路，$0≤C_i≤10,000$;然而航线的花费很神奇，花费 $C_i$ 可能是负数$(−10,000≤Ci≤10,000)$。
**道路是双向的**，可以从 $A_i$ 到 $B_i$，也可以从 $B_i$ 到 $A_i$，花费都是 $C_i$。
然而 **航线与之不同**，只可以从 $A_i$ 到 $B_i$。
事实上，由于最近恐怖主义太嚣张，为了社会和谐，出台了一些政策：
保证如果有一条航线可以从 $A_i$ 到 $B_i$，那么保证不可能通过一些道路和航线从$B_i$ 回到 $A_i$。
由于约翰的奶牛世界公认十分给力，他需要运送奶牛到每一个城镇。
他想找到从发送中心城镇 $S$ **把奶牛送到每个城镇的最便宜的方案**。
**输入格式**
第一行包含四个整数 $T,R,P,S$。
接下来 $R$ 行，每行包含三个整数（表示一个道路）$A_i,B_i,C_i$。
接下来 $P$ 行，每行包含三个整数（表示一条航线）$A_i,B_i,C_i$。
**输出格式**
第 $1..T$ 行：第 $i$ 行输出从 $S$ 到达城镇 $i$ 的最小花费，如果不存在，则输出 `NO PATH`。
### 二、$Dijkstra$不能处理负权边，但可以处理负权初值
我们说了$Dijkstra$算法不能解决带有负权边的图，这是为什么呢？下面用一个例子讲解一下
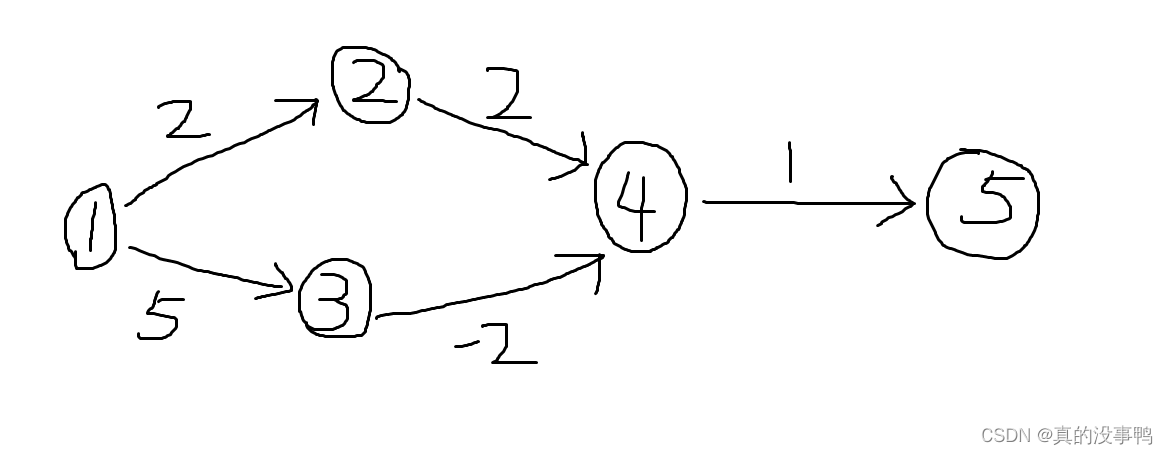
以这里图为例，一共有五个点，也就说要循环$5$次，确定每个点的最短距离
用$Dijkstra$算法解决的的详细步骤
> 1. 初始$dist[1] = 0$，$1$号点距离起点$1$的距离为$0$
> 2. 找到了未标识且离起点$1$最近的结点$1$，标记$1$号点，用$1$号点更新和它相连点的距离，$2$号点被更新成$dist[2] = 2$，$3$号点被更新成$dist[3] = 5$
> 3. 找到了未标识且离起点$1$最近的结点$2$，标识$2$号点，用$2$号点更新和它相连点的距离，$4$号点被更新成$dist[4] = 4$
> 4. 找到了未标识且离起点$1$最近的结点$4$，标识$4$号点，用$4$号点更新和它相连点的距离，$5$号点被更新成$dist[5] = 5$
> 5. 找到了未标识且离起点$1$最近的结点$3$，标识$3$号点，用$3$号点更新和它相连点的距离，$4$号点被更新成$dist[4] = 3$
>
**结果**
> $Dijkstra$算法在图中走出来的最短路径是$1 -> 2 -> 4 -> 5$，算出 $1$ 号点到$5$ 号点的最短距离是$2 + 2 + 1 = 5$，然而还存在一条路径是$1 -> 3 -> 4 -> 5$，该路径的长度是$5 + (-2) + 1 = 4$
> 因此 $dijkstra$ 算法 **失效**
**总结**
> 我们可以发现如果有负权边的话$4$号点经过标记后还可以继续更新
但此时$4$号点已经被标记过了，所以$4$号点不能被更新了，只能一条路走到黑
当用负权边更新$4$号点后$5$号点距离起点的距离我们可以发现可以进一步缩小成$4$。
所以总结下来就是:$dijkstra$**不能解决负权边** 是因为 $dijkstra$要求每个点被确定后，$dist[j]$就是最短距离了，之后就不能再被更新了（**一锤子买卖**），而如果有负权边的话，那已经确定的点的$dist[j]$不一定是最短了，可能还可以通过负权边进行更新。
**负权初始值**
那如果不是负权的边长，而是负权的初值呢？这个就没关系了，因为初值不影响算法逻辑，不信你看下有好多算法题都是判断$INF/2$,正无穷不也是在过程中松弛操作更改过吗，你是负的初始值也是没有问题，可以正确运行算法。
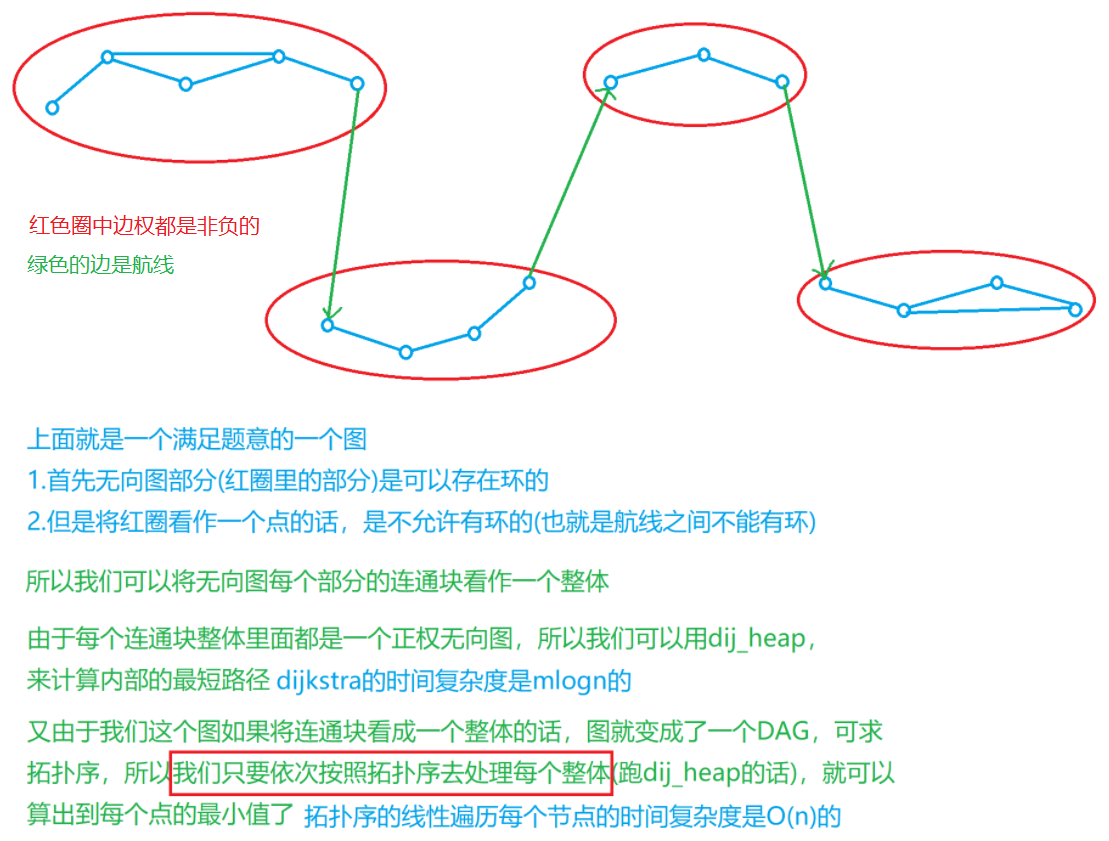
### 三、拓扑序+$Dijkstra$ + 缩点
* ① 分析题目可知城镇内部之间的权值是非负的，内部可以使用$dijkstra$算法
* ② 城镇之间的航线 **有负权**，不能用$Dijkstra$。虽然$SFPA$可以搞定负权，但记住它已经死了，不考虑它~
* ③ 如果有严格的顺序关系，即拓扑序，按照 **城镇拓扑序的关系**,是可以使用$Dijkstra$的，原因如下：
每个城镇称为一个 **团**，按照 **拓扑序** 遍历到某个团时，**此时该团中城市的距离不会再被其它团更新**，因此可以 **按照拓扑序** **依次** 运行 $dijkstra$ 算法
#### 算法步骤
#### $Code$
```cpp {.line-numbers}
#include
using namespace std;
const int N = 25010, M = 150010;
const int INF = 0x3f3f3f3f;
typedef pair PII;
// 存图
int idx, h[N], e[M], w[M], ne[M];
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int T; // 城镇数量
int R; // 道路数量
int P; // 航线数量
int S; // 出发点
// 下面两个数组是一对
int id[N]; // 节点在哪个连通块中
vector block[N]; // 连通块包含哪些节点
int bcnt; // 连通块序号计数器
int dist[N]; // 最短距离(结果数组)
int in[N]; // 每个DAG(节点即连通块)的入度
bool st[N]; // dijkstra用的是不是在队列中的数组
queue q; // 拓扑序用的队列
// 将u节点加入团中,团的番号是 bid
void dfs(int u, int bid) {
id[u] = bid; // ① u节点属于bid团
block[bid].push_back(u); // ② 记录bid团包含u节点
// 枚举u节点的每一条出边，将对端的城镇也加入到bid这个团中
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!id[v]) dfs(v, bid); // Flood Fill
}
}
// 计算得到bid这个连通块中最短距离
void dijkstra(int bid) {
priority_queue, greater> pq;
/*
因为不确定连通块内的哪个点可以作为起点，所以就一股脑全加进来就行了，
反正很多点的dist都是inf（这些都是不能成为起点的）,那么可以作为起点的就自然出现在堆顶了
因为上面的写法把拓扑排序和dijkstra算法拼在一起了，如果不把所有点都加入堆，
会导致后面其他块的din[]没有减去前驱边，从而某些块没有被拓扑排序遍历到。
*/
for (auto u : block[bid]) pq.push({dist[u], u});
while (pq.size()) {
int u = pq.top().second;
pq.pop();
if (st[u]) continue;
st[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (st[v]) continue;
if (dist[v] > dist[u] + w[i]) {
dist[v] = dist[u] + w[i];
// 如果是同团中的道路,需要再次进入Dijkstra的小顶堆，以便计算完整个团中的路径最小值
if (id[u] == id[v]) pq.push({dist[v], v});
}
/*如果u和v不在同一个团中,说明遍历到的是航线
此时，需要与拓扑序算法结合，尝试剪掉此边，是不是可以形成入度为的团
id[v]:v这个节点所在的团番号
--in[id[v]] == 0: u->v是最后一条指向团id[v]的边，此边拆除后，id[v]这个团无前序依赖，稳定了，
可以将此团加入拓扑排序的queue队列中，继续探索
*/
if (id[u] != id[v] && --in[id[v]] == 0) q.push(id[v]);
}
}
}
// 拓扑序
void topsort() {
for (int i = 1; i <= bcnt; i++) // 枚举每个团
if (!in[i]) q.push(i); // 找到所有入度为0的团,DAG的起点
// 拓扑排序
while (q.size()) {
int bid = q.front(); // 团番号
q.pop();
// 在此团内部跑一遍dijkstra
dijkstra(bid);
}
}
int main() {
memset(h, -1, sizeof h); // 初始化
scanf("%d %d %d %d", &T, &R, &P, &S); // 城镇数量,道路数量,航线数量,出发点
memset(dist, 0x3f, sizeof dist); // 初始化最短距离
dist[S] = 0; // 出发点距离自己的长度是0,其它的最短距离目前是INF
int a, b, c; // 起点，终点，权值
while (R--) { // 读入道路
scanf("%d %d %d", &a, &b, &c);
add(a, b, c), add(b, a, c); // 连通块内是无向图
}
/* 航线本质是 团与团 之间单向连接边
外部是DAG有向无环图，局部是内部双向正权图
为了建立外部的DAG有向无环图，我们需要给每个团分配一个番号，记为bid;
同时，也需要知道每个团内，有哪些小节点:
(1) id[i]:节点i隶属于哪个团(需要提前准备好团的番号)
(2) vector block[N] :每个团中有哪些节点
Q:一共几个团呢？每个团中都有谁呢？谁都在哪个图里呢？
A:在没有录入航线的情况下，现在图中只有 大块孤立 但 内部连通 的节点数据，
可以用dfs进行Flood Fill,发现没有团标识的节点，就创建一个新的团番号，
并且记录此节点加入了哪个团，记录哪个团有哪些点。
注意：需要在未录入航线的情况下统计出团与节点的关系，否则一会再录入航线，就没法找出哪些节点在哪个团里了
*/
// 缩点
for (int i = 1; i <= T; i++) // 枚举每个小节点
if (!id[i]) // 如果它还没有标识是哪个团,就开始研究它，把它标识上隶属于哪个团，并且，把和它相连接的其它点也加入同一个团中
dfs(i, ++bcnt); // 需要提前申请好番号bcnt
// 航线
while (P--) {
scanf("%d %d %d", &a, &b, &c);
add(a, b, c); // 单向边
in[id[b]]++; // b节点所在团入度+1
}
// 拓扑序
topsort();
// 从S到达城镇i的最小花费
for (int i = 1; i <= T; i++) {
if (dist[i] > INF / 2)
puts("NO PATH");
else
cout << dist[i] << endl;
}
return 0;
}
```