HDU 1730 Northcott Game
[题目传送门](https://acm.hdu.edu.cn/showproblem.php?pid=1730)
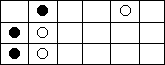
图1 图2
图2
 ### 一、解题思路
* 把同一行棋子之间的距离看做石子数。两个棋子紧挨着,就表示这堆石子个数为零。否则石子数量就是白色棋子坐标与黑色棋子坐标差+1。
* 如果黑棋选择扩大距离(向左走)
白棋足够聪明,直接跟进,贴上黑棋,这样,本行黑棋不管怎么操作,都会被跟进,直到遇到左侧边界,那么,黑棋将在本行无路可走,只能再去其它行尝试,也就是黑棋在本行没有占到便宜,被迫进入下一行。换句话说,在本题中不能扩大距离,只能缩小距离,即拿走一些石子。
* 如果黑棋选择缩小距离(向右走)
对比Nim游戏,就是拿走一些石子,一共有N堆石子,每次只能从某一堆中拿走一些石子(`>=1 && <=a[i]`)个。问是先手必胜,还是先手必败,这不就是经典的Nim游戏吗?
直接以坐标差$+1$做为石子个数,构建$Nim$游戏,计算异或和,是$0$则先手必败,否则先手必胜。
### 二、模拟第二组数据, 黑棋是怎么赢的
```c++
#include
using namespace std;
int main() {
int res = 2 ^ 0 ^ 0;
printf("%d\n", res); //异或和
printf("%d\n", res ^ 2); //剩余几个 输出0
printf("%d\n", 2 - (res ^ 2)); //取走几个 输出2
return 0;
}
```
### 三、实现代码
```c++
#include
using namespace std;
int main() {
int n, m;
while (~scanf("%d %d", &n, &m)) {
int res = 0;
for (int i = 1; i <= n; ++i) {
int a, b;
scanf("%d %d", &a, &b);
res = res ^ (abs(a - b) - 1);
}
if (res == 0)
puts("BAD LUCK!");
else
puts("I WIN!");
}
return 0;
}
```
### 一、解题思路
* 把同一行棋子之间的距离看做石子数。两个棋子紧挨着,就表示这堆石子个数为零。否则石子数量就是白色棋子坐标与黑色棋子坐标差+1。
* 如果黑棋选择扩大距离(向左走)
白棋足够聪明,直接跟进,贴上黑棋,这样,本行黑棋不管怎么操作,都会被跟进,直到遇到左侧边界,那么,黑棋将在本行无路可走,只能再去其它行尝试,也就是黑棋在本行没有占到便宜,被迫进入下一行。换句话说,在本题中不能扩大距离,只能缩小距离,即拿走一些石子。
* 如果黑棋选择缩小距离(向右走)
对比Nim游戏,就是拿走一些石子,一共有N堆石子,每次只能从某一堆中拿走一些石子(`>=1 && <=a[i]`)个。问是先手必胜,还是先手必败,这不就是经典的Nim游戏吗?
直接以坐标差$+1$做为石子个数,构建$Nim$游戏,计算异或和,是$0$则先手必败,否则先手必胜。
### 二、模拟第二组数据, 黑棋是怎么赢的
```c++
#include
using namespace std;
int main() {
int res = 2 ^ 0 ^ 0;
printf("%d\n", res); //异或和
printf("%d\n", res ^ 2); //剩余几个 输出0
printf("%d\n", 2 - (res ^ 2)); //取走几个 输出2
return 0;
}
```
### 三、实现代码
```c++
#include
using namespace std;
int main() {
int n, m;
while (~scanf("%d %d", &n, &m)) {
int res = 0;
for (int i = 1; i <= n; ++i) {
int a, b;
scanf("%d %d", &a, &b);
res = res ^ (abs(a - b) - 1);
}
if (res == 0)
puts("BAD LUCK!");
else
puts("I WIN!");
}
return 0;
}
```

