## [$AcWing$ $378$. 骑士放置](https://www.acwing.com/problem/content/380/)
### 一、题目描述
给定一个 $N×M$ 的棋盘,有一些格子禁止放棋子。
问棋盘上最多能放多少个不能互相攻击的骑士(国际象棋的“ **骑士** ”,类似于中国象棋的“ **马** ”,按照“ **日** ”字攻击,但没有中国象棋“ **别马腿** ”的规则)。
**输入格式**
第一行包含三个整数 $N,M,T$,其中 $T$ 表示禁止放置的格子的数量。
接下来 $T$ 行每行包含两个整数 $x$ 和 $y$,表示位于第 $x$ 行第 $y$ 列的格子禁止放置,行列数从 $1$ 开始。
**输出格式**
输出一个整数表示结果。
**数据范围**
$1≤N,M≤100$
**输入样例**:
```cpp {.line-numbers}
2 3 0
```
**输出样例:**
```cpp {.line-numbers}
4
```
### 二、解题思路
#### 前置知识
图论基础之二分图中 **最小覆盖问题** 的求解思路
#### 最大独立集
「**图的最大独立集**」:从图中选出「**最多**」的点,使得「**选出的点中 任意两点之间没有边**」。
「**图的最大团**」:从图中选出「**最多**」的点,使得「**选出的 任意两点之间都有边**」。
根据定义,我们也能发现,这两个概念是「**互补**」的。「**补图**」:就是把原图中所有边拆开,所有未连接的边连上。
那么,「**原图中的最大独立集就是补图中的最大团**」。
#### 二分图中求最大独立集
(前提条件是必须「**在二分图中**」下面的性质才能成立!!!)
首先,明确目标是「我们要选出最多的点,使得选出点中,任意两点之间是没有边的」,等价于是「**选出最少的点**,假如消除这些点,会使图中不存在任何一条边,我们**把这些点去掉,剩下的就构成了最大独立集**」。
这里有点脑筋急转弯,当我们「把 **二分图中** 所有能构成边的点 **去掉**,那么剩下的点 **就一定没法** 再构成任何一条边」,而我们的目标是让「剩下的点最多」,那么「去掉的点就应该最少」。
而「选出最少的点,使这些点能构成所有的边」,其实就是我们前置文章中的概念「最小覆盖点集」。并且在前置文章中,我们已经知道「**在二分图中,最小覆盖点集就等价于最大匹配数量**」。
因此,我们就得出了「二分图中最大独立点集」的求法:「只需要求出最大匹配,然后用总点数减去最大匹配数」即可。

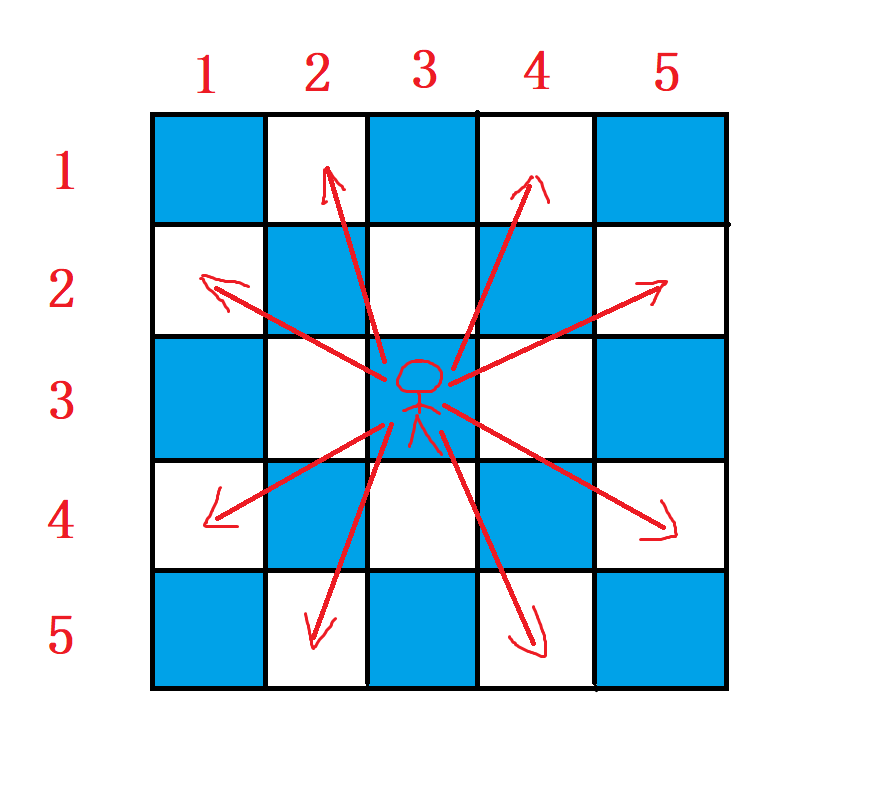 如果我们把每个格子看做一个点,如果能从该格子能跳到另一个格子,则两个格子之间连接一条边。
进而,我们发现「如果把格子按照坐标进行 **奇偶** 划分为两个集合,那么能连边的两个点一定在不同集合,所以整个棋盘会形成一个 **二分图**」。
根据上述模型,我们可以把题目的问题「最多可以放多少个不能互相攻击的棋子」变成「棋盘上最多可以有多少个棋子之间没有边」,也就是求「**最大独立集**」。
如果我们把每个格子看做一个点,如果能从该格子能跳到另一个格子,则两个格子之间连接一条边。
进而,我们发现「如果把格子按照坐标进行 **奇偶** 划分为两个集合,那么能连边的两个点一定在不同集合,所以整个棋盘会形成一个 **二分图**」。
根据上述模型,我们可以把题目的问题「最多可以放多少个不能互相攻击的棋子」变成「棋盘上最多可以有多少个棋子之间没有边」,也就是求「**最大独立集**」。
 ### 三、实现代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 100 * 100 + 10, M = 8 * N; // 注意点的数量,每个点最多8个方向
// 链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
// 棋盘专用dx8
int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};
int n, m, k;
int g[110][110]; // 禁止放置的位置
// 匈牙利算法专用数组
int match[N], st[N];
int dfs(int u) {
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!st[v]) {
st[v] = 1;
if (!match[v] || dfs(match[v])) {
match[v] = u;
return 1;
}
}
}
return 0;
}
int main() {
#ifndef ONLINE_JUDGE
freopen("378.in", "r", stdin);
#endif
// 初始化链式前向星
memset(h, -1, sizeof h);
scanf("%d %d %d", &n, &m, &k);
// 不可以放置的位置记录
for (int i = 1; i <= k; i++) {
int x, y;
scanf("%d %d", &x, &y);
g[x][y] = 1;
}
// 使用链式前向星建图
vector vec;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
if ((i + j) % 2 && !g[i][j]) { // 横纵坐标和为奇数,并且,此位置没有被禁止
int id = (i - 1) * m + j;
vec.push_back(id);
for (int k = 0; k < 8; k++) { // 8个方向建边
int tx = i + dx[k], ty = j + dy[k];
int tid = (tx - 1) * m + ty;
if (tx < 1 || tx > n || ty < 1 || ty > m) continue; // 出界不要
if (g[tx][ty]) continue; // 被禁止不行
add(id, tid); // 建边,注意一下二维坐标与点号的映射关系。同时,由于正反都可以创建,这里就不用一次建两条
}
}
}
int res = 0;
for (auto id : vec) {
memset(st, 0, sizeof st);
if (dfs(id)) res++; // 开始跑匈牙利算法
}
// 最大独立集 n-无法放的点-最大匹配数
printf("%d\n", n * m - k - res);
return 0;
}
```
### 三、实现代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 100 * 100 + 10, M = 8 * N; // 注意点的数量,每个点最多8个方向
// 链式前向星
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
// 棋盘专用dx8
int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};
int n, m, k;
int g[110][110]; // 禁止放置的位置
// 匈牙利算法专用数组
int match[N], st[N];
int dfs(int u) {
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!st[v]) {
st[v] = 1;
if (!match[v] || dfs(match[v])) {
match[v] = u;
return 1;
}
}
}
return 0;
}
int main() {
#ifndef ONLINE_JUDGE
freopen("378.in", "r", stdin);
#endif
// 初始化链式前向星
memset(h, -1, sizeof h);
scanf("%d %d %d", &n, &m, &k);
// 不可以放置的位置记录
for (int i = 1; i <= k; i++) {
int x, y;
scanf("%d %d", &x, &y);
g[x][y] = 1;
}
// 使用链式前向星建图
vector vec;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
if ((i + j) % 2 && !g[i][j]) { // 横纵坐标和为奇数,并且,此位置没有被禁止
int id = (i - 1) * m + j;
vec.push_back(id);
for (int k = 0; k < 8; k++) { // 8个方向建边
int tx = i + dx[k], ty = j + dy[k];
int tid = (tx - 1) * m + ty;
if (tx < 1 || tx > n || ty < 1 || ty > m) continue; // 出界不要
if (g[tx][ty]) continue; // 被禁止不行
add(id, tid); // 建边,注意一下二维坐标与点号的映射关系。同时,由于正反都可以创建,这里就不用一次建两条
}
}
}
int res = 0;
for (auto id : vec) {
memset(st, 0, sizeof st);
if (dfs(id)) res++; // 开始跑匈牙利算法
}
// 最大独立集 n-无法放的点-最大匹配数
printf("%d\n", n * m - k - res);
return 0;
}
```

