##[$AcWing$ $423$. 采药](https://www.acwing.com/problem/content/425/)

### 一、题目描述
辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。

为此，他想拜附近最有威望的医师为师。

医师为了判断他的资质，给他出了一个难题。

医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以**让采到的草药的总价值最大**。”

如果你是辰辰，你能完成这个任务吗？

**输入格式**
输入文件的第一行有两个整数 $T$ 和 $M$，用一个空格隔开，$T$ 代表总共能够用来采药的时间，$M$ 代表山洞里的草药的数目。

接下来的 $M$ 行每行包括两个在 $1$ 到 $100$ 之间（包括 $1$ 和 $100$）的整数，分别表示 **采摘某株草药的时间** 和 **这株草药的价值**。

**输出格式**
输出文件包括一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

**数据范围**
$1≤T≤1000$,$1≤M≤100$

**输入样例**：
```cpp {.line-numbers}
70 3
71 100
69 1
1 2
```

**输出样例**：
```cpp {.line-numbers}
3
```


### 二、题目解析

**01背包模型**

**状态表示**

$f(i,j)$
- **集合**
考虑前 $i$ 个物品，且当前已使用体积为$ j$ 的方案
- **属性** 
该方案的价值为最大值 $max$

**状态转移$f(i,j)$**： 

$$f(i,j)=\begin{equation}
            \left\{
                 \begin{array}{lr}
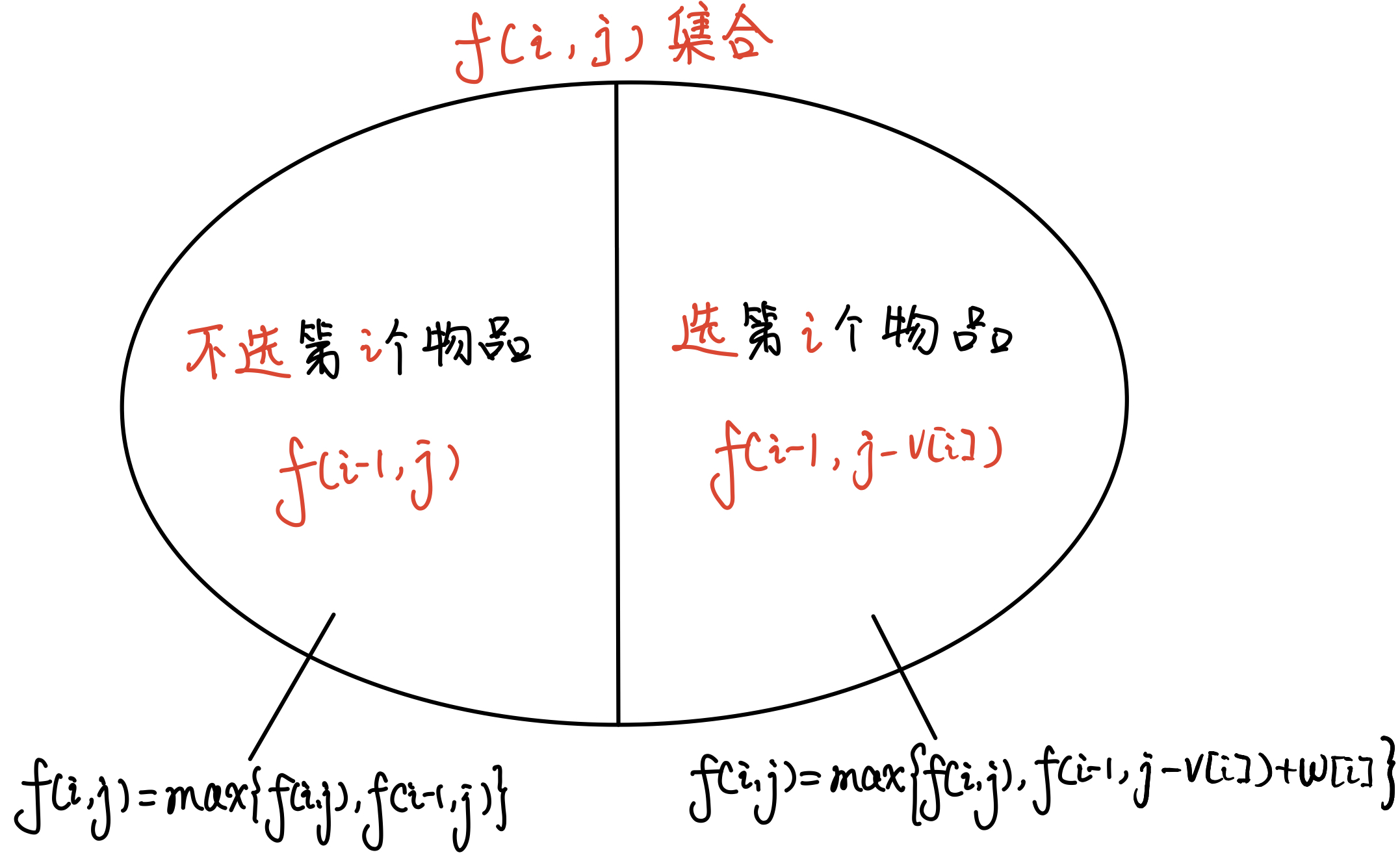
                 不选第i个物品: f(i-1,j) &  \\
                 选第i个物品: max\{f(i,j),f(i-1,j-w_i)+v_i\}\\
                 \end{array}
            \right.
 \end{equation}$$

初始状态：`f[0][0]`

目标状态：`f[n][m]`

**集合划分**
<center><img src='https://cdn.acwing.com/media/article/image/2021/06/10/55909_2253c174c9-IMG_BC60906447BB-1.jpeg'></center>


### 三、二维朴素作法
时间复杂度：$O(n×m)$

```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int N = 110;
const int M = 1010;

int n, m;
int w[N], v[N];
int f[N][M];

int main() {
    cin >> m >> n;

    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) {
            f[i][j] = f[i - 1][j]; // 不选
            if (j >= v[i])
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]); // 选
        }
    printf("%d\n", f[n][m]);
    return 0;
}

```

### 四、一维优化
```cpp {.line-numbers}
#include <bits/stdc++.h>

using namespace std;
const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main() {
    cin >> m >> n;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    // 01背包模板
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    printf("%d\n", f[m]);
    return 0;
}
```