## $KMP$算法
### 一、$KMP$是做什么用的?
$KMP$全称为$Knuth$ $Morris$ $Pratt$算法,三个单词分别是三个作者的名字。$KMP$是一种高效的字符串匹配算法,用来在主字符串中查找模式字符串的位置(比如在“$hello,world$”主串中查找“$world$”模式串的位置)。
### 二、$KMP$算法的高效体现在哪?
高效性是通过和其他字符串搜索算法对比得到的,在这里拿暴力朴素算法做一下对比。主要的思想是在主串的$[0, n-m]$区间内依次截取长度为$m$的子串,看子串是否和模式串一样($n$是主串的长度,$m$是子串的长度)。举个例子如下:给定文本串$S$,“$aaaababaaba$”,和模式串$P$,“$ababa$”,现在要拿模式串$P$去跟文本串$S$匹配,整个过程如下所示:

**动画展示**
 暴力算法的时间复杂度是$O(N*N)$,存在很大优化空间。当模式串和主串匹配时,遇到模式串中某个字符不能匹配的情况,对于模式串中已经匹配过的那些字符,如果我们能找到一些规律,将模式串多往后移动几位,而不是像暴力算法算法一样,每次把模式串移动一位,就可以提高算法的效率。
$kmp$算法给我们提供的思路是:对于模式串,将每一个字符在匹配失败时可以向后移动的最大距离保存在一个$prefix$数组中,有的也叫$next$数组。这样当匹配失败时就可以按照$prefix$数组中保存的数字向后多移动几位。从而提高算法的效率。
#### 动画展示
暴力算法的时间复杂度是$O(N*N)$,存在很大优化空间。当模式串和主串匹配时,遇到模式串中某个字符不能匹配的情况,对于模式串中已经匹配过的那些字符,如果我们能找到一些规律,将模式串多往后移动几位,而不是像暴力算法算法一样,每次把模式串移动一位,就可以提高算法的效率。
$kmp$算法给我们提供的思路是:对于模式串,将每一个字符在匹配失败时可以向后移动的最大距离保存在一个$prefix$数组中,有的也叫$next$数组。这样当匹配失败时就可以按照$prefix$数组中保存的数字向后多移动几位。从而提高算法的效率。
#### 动画展示
 ### 三、什么是前缀数组$prefix$
在$KMP$算法中有个关键的数组,叫做前缀数组,也有的叫$next$数组,每一个子串有一个固定的$next$数组,它记录着字符串匹配过程中失配情况下可以向后多跳几个字符,其实也是子串的前缀和后缀相同的最长长度。说不明白,上图:
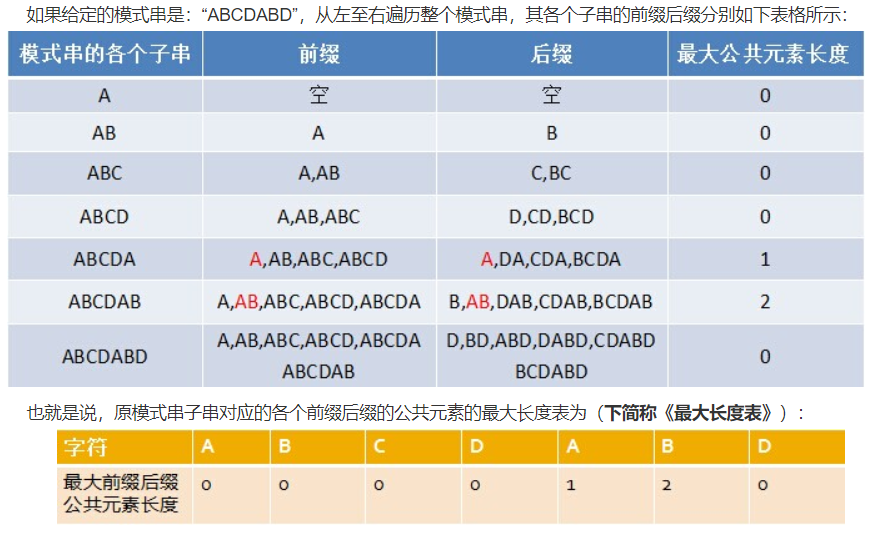
怎么求这个数组我们放在最后说,先说怎么使用这个前缀数组来实现$kmp$算法
### 四、算法思路
思路好像也已经说过了,就是在暴力的算法的基础上,在匹配失败的时候往后多跳几位,而跳几位保存在前缀数组中。接下来我们看一下原理是什么样的,为什么前缀数组就可以作为跳几步的依据。
举个例子,下图中已经写好了总串$s$和模式串$p$,模式串的前缀数组为$[0,0,1,2,3]$,且所以下标都是从$1$开始。看图中当$i=8,j=4$时$s[i] != p[j + 1]$,即将要匹配失败了,图中红色圈住的是子串的后缀。黄圈圈住的是前缀。蓝色圈圈住的是已经和后缀匹配过的部分,那么下一次将模式串后移$prefix[j]=2$位时,原来的前缀正好对着蓝色圈圈部分,因为前缀=后缀=蓝色圈圈部分,所以移动后的橙色部分就不用再判断了。
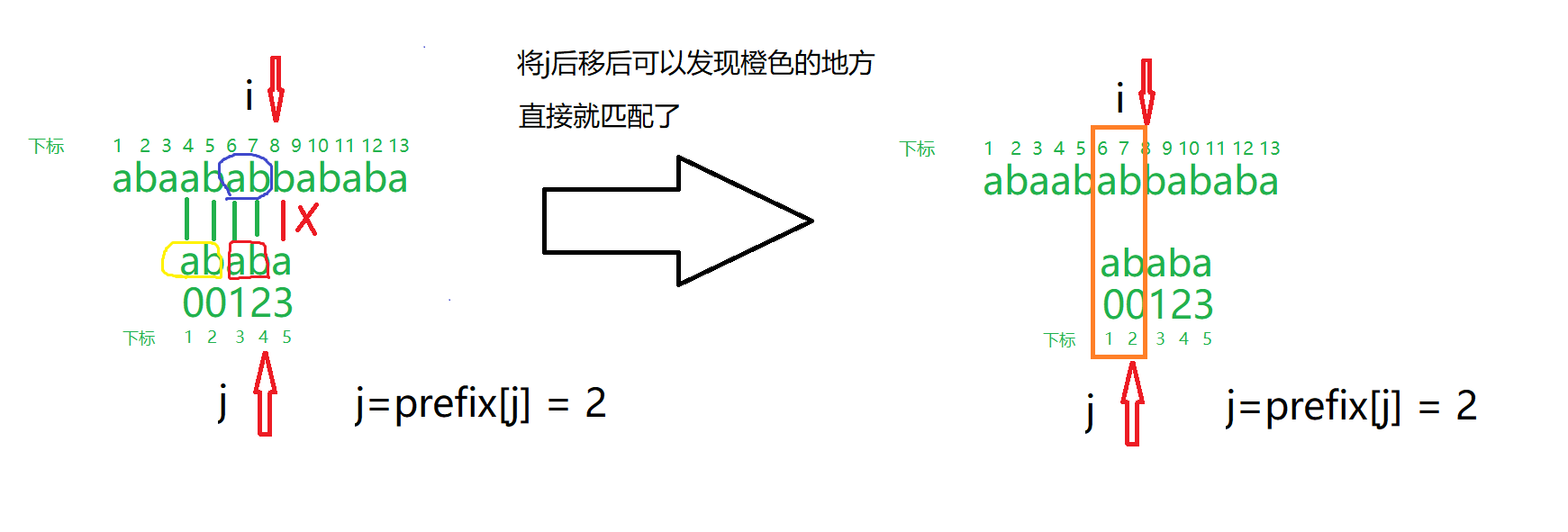
再用上一个双指针算法思路。$i$遍历总串$s$,$j$遍历模式串$p$,判断$s[i]$ 和 $p[j + 1]$是否匹配。不匹配就将$j$重置为前缀数组中$prefix[j]$的值。匹配的话$j$往后移动一位。当匹配了$n$个字符后即代表完全匹配。此时答案即为$i-n$,如果要继续搜索,要将$j$再置为$prefix[j]$。
为了方便写代码所有数组的下标都从$1$开始
```cpp {.line-numbers}
// 求源串中模式串出现的每个位置
for (int i = 1, j = 0; i <= m; i++) {
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j++;
if (j == n) {
printf("%d ", i - n);
j = ne[j]; // 继续搜索,重置 j=ne[j]
}
}
```
### 五、怎么求前缀数组?
前缀数组是$kmp$里面最难的部分,网上也有很多种求法。比如利用后一个元素和前面的元素之间存在数学公式关系来求,我们这里使用的方式是和上面的匹配过程类似的方法,也就是将前缀看作模式串,在$p$中匹配他。也就是字符串$p$自己找自己的匹配串。
### 六、实现代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1000010;
int n, m, ne[N];
char s[N], p[N];
int main() {
cin >> n >> (p + 1) >> m >> (s + 1);
// 一、求ne数组
// i:当前试图进行匹配的S串字符,j+1是模板串当前试图与S串i位置进行匹配的字符
// j:表示已匹配的长度,一直都在尝试让j+1位和i位进行匹配,退无可退,无需再退。
// i:是从2开始的,因为ne[1]=0,表示第1个不匹配,只能重头开始,不用算
for (int i = 2, j = 0; i <= n; i++) {
while (j && p[i] != p[j + 1]) j = ne[j];
// 如果是匹配情况发生了,那么j移动到下一个位置
if (p[i] == p[j + 1]) j++;
// 记录j到ne数组中
ne[i] = j;
}
// 二、匹配字符串
// i:当前试图进行对比的S串位置
// j:最后一个已完成匹配的P串位置,那么,当前试图与S串当前位置i进行尝试对比匹配的位置是j+1
for (int i = 1, j = 0; i <= m; i++) {
while (j && s[i] != p[j + 1]) j = ne[j]; // 不行就退吧,当j==0时,表示退无可退,无需再退
// 如果是匹配情况发生了,那么j移动到下一个位置
if (s[i] == p[j + 1]) j++; // 匹配则指针前行,i不用++,因为它在自己的for循环中,自带++
if (j == n) { // 如果匹配到最大长度,说明完成了所有位置匹配
printf("%d ", i - n); // 输出开始匹配位置
j = ne[j]; // 回退,尝试继续进行匹配,看看还有没有其它可以匹配的位置
}
}
return 0;
}
```
### 七、练习题
**[洛谷 $P3375$ 【模板】](https://www.luogu.com.cn/problem/P3375)**
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1000010;
int n, m, ne[N];
char s[N], p[N];
int main() {
#ifndef ONLINE_JUDGE
freopen("P3375.in", "r", stdin);
#endif
cin >> (s + 1) >> (p + 1); // 先长串,再短串
n = strlen(p + 1), m = strlen(s + 1); // 自已来测长
// 求模式串ne数组
for (int i = 2, j = 0; i <= n; i++) {
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j++;
ne[i] = j;
}
// 求源串中模式串出现的每个位置
for (int i = 1, j = 0; i <= m; i++) {
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j++;
if (j == n) {
printf("%d\n", i - n + 1);
j = ne[j]; // 继续搜索,重置 j=ne[j]
}
}
// 本题要求最后输出模式串的ne数组
for (int i = 1; i <= n; i++) cout << ne[i] << " ";
return 0;
}
```
**[洛谷 $P4391$ [$BOI2009$]$Radio$ $Transmission$ 无线传输](https://www.luogu.com.cn/problem/P4391)**
这道题是$KMP$的经典应用:**求循环节**。
根据$next$数组的性质,我们可以知道一个字符串前缀等于后缀的最大长度$l$,这字符串全长为$L$ ,那么这个字符串的循环节长度就是 $L - l$。
为什么是这样呢?看下面这张图就很容易理解了。
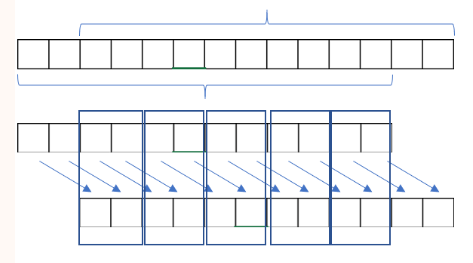
很显然,这个字符串的循环节长度为$2$。
**解释**:
设字串长度为 $x$,字符串从 $1$ 开始计数
$next[1]=next[2]=……next[x]=0$
$next[x+1]=1 next[x+n]=n$
发现从 $x+1$ 位置开始,$next$ 数组逐渐递增 $1$
所以答案为 $n-next[n]$
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1000010;
int n, ne[N];
char p[N];
int main() {
cin >> n >> (p + 1);
// 求模式串ne数组
for (int i = 2, j = 0; i <= n; i++) {
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j++;
ne[i] = j;
}
printf("%d", n - ne[n]);
return 0;
}
```
### 八、参考资料
**[代码随想录的理论篇](https://www.bilibili.com/video/BV1PD4y1o7nd)**
**[代码随想录的代码篇](https://www.bilibili.com/video/BV1M5411j7Xx)**
### 三、什么是前缀数组$prefix$
在$KMP$算法中有个关键的数组,叫做前缀数组,也有的叫$next$数组,每一个子串有一个固定的$next$数组,它记录着字符串匹配过程中失配情况下可以向后多跳几个字符,其实也是子串的前缀和后缀相同的最长长度。说不明白,上图:

怎么求这个数组我们放在最后说,先说怎么使用这个前缀数组来实现$kmp$算法
### 四、算法思路
思路好像也已经说过了,就是在暴力的算法的基础上,在匹配失败的时候往后多跳几位,而跳几位保存在前缀数组中。接下来我们看一下原理是什么样的,为什么前缀数组就可以作为跳几步的依据。
举个例子,下图中已经写好了总串$s$和模式串$p$,模式串的前缀数组为$[0,0,1,2,3]$,且所以下标都是从$1$开始。看图中当$i=8,j=4$时$s[i] != p[j + 1]$,即将要匹配失败了,图中红色圈住的是子串的后缀。黄圈圈住的是前缀。蓝色圈圈住的是已经和后缀匹配过的部分,那么下一次将模式串后移$prefix[j]=2$位时,原来的前缀正好对着蓝色圈圈部分,因为前缀=后缀=蓝色圈圈部分,所以移动后的橙色部分就不用再判断了。

再用上一个双指针算法思路。$i$遍历总串$s$,$j$遍历模式串$p$,判断$s[i]$ 和 $p[j + 1]$是否匹配。不匹配就将$j$重置为前缀数组中$prefix[j]$的值。匹配的话$j$往后移动一位。当匹配了$n$个字符后即代表完全匹配。此时答案即为$i-n$,如果要继续搜索,要将$j$再置为$prefix[j]$。
为了方便写代码所有数组的下标都从$1$开始
```cpp {.line-numbers}
// 求源串中模式串出现的每个位置
for (int i = 1, j = 0; i <= m; i++) {
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j++;
if (j == n) {
printf("%d ", i - n);
j = ne[j]; // 继续搜索,重置 j=ne[j]
}
}
```
### 五、怎么求前缀数组?
前缀数组是$kmp$里面最难的部分,网上也有很多种求法。比如利用后一个元素和前面的元素之间存在数学公式关系来求,我们这里使用的方式是和上面的匹配过程类似的方法,也就是将前缀看作模式串,在$p$中匹配他。也就是字符串$p$自己找自己的匹配串。
### 六、实现代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1000010;
int n, m, ne[N];
char s[N], p[N];
int main() {
cin >> n >> (p + 1) >> m >> (s + 1);
// 一、求ne数组
// i:当前试图进行匹配的S串字符,j+1是模板串当前试图与S串i位置进行匹配的字符
// j:表示已匹配的长度,一直都在尝试让j+1位和i位进行匹配,退无可退,无需再退。
// i:是从2开始的,因为ne[1]=0,表示第1个不匹配,只能重头开始,不用算
for (int i = 2, j = 0; i <= n; i++) {
while (j && p[i] != p[j + 1]) j = ne[j];
// 如果是匹配情况发生了,那么j移动到下一个位置
if (p[i] == p[j + 1]) j++;
// 记录j到ne数组中
ne[i] = j;
}
// 二、匹配字符串
// i:当前试图进行对比的S串位置
// j:最后一个已完成匹配的P串位置,那么,当前试图与S串当前位置i进行尝试对比匹配的位置是j+1
for (int i = 1, j = 0; i <= m; i++) {
while (j && s[i] != p[j + 1]) j = ne[j]; // 不行就退吧,当j==0时,表示退无可退,无需再退
// 如果是匹配情况发生了,那么j移动到下一个位置
if (s[i] == p[j + 1]) j++; // 匹配则指针前行,i不用++,因为它在自己的for循环中,自带++
if (j == n) { // 如果匹配到最大长度,说明完成了所有位置匹配
printf("%d ", i - n); // 输出开始匹配位置
j = ne[j]; // 回退,尝试继续进行匹配,看看还有没有其它可以匹配的位置
}
}
return 0;
}
```
### 七、练习题
**[洛谷 $P3375$ 【模板】](https://www.luogu.com.cn/problem/P3375)**
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1000010;
int n, m, ne[N];
char s[N], p[N];
int main() {
#ifndef ONLINE_JUDGE
freopen("P3375.in", "r", stdin);
#endif
cin >> (s + 1) >> (p + 1); // 先长串,再短串
n = strlen(p + 1), m = strlen(s + 1); // 自已来测长
// 求模式串ne数组
for (int i = 2, j = 0; i <= n; i++) {
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j++;
ne[i] = j;
}
// 求源串中模式串出现的每个位置
for (int i = 1, j = 0; i <= m; i++) {
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j++;
if (j == n) {
printf("%d\n", i - n + 1);
j = ne[j]; // 继续搜索,重置 j=ne[j]
}
}
// 本题要求最后输出模式串的ne数组
for (int i = 1; i <= n; i++) cout << ne[i] << " ";
return 0;
}
```
**[洛谷 $P4391$ [$BOI2009$]$Radio$ $Transmission$ 无线传输](https://www.luogu.com.cn/problem/P4391)**
这道题是$KMP$的经典应用:**求循环节**。
根据$next$数组的性质,我们可以知道一个字符串前缀等于后缀的最大长度$l$,这字符串全长为$L$ ,那么这个字符串的循环节长度就是 $L - l$。
为什么是这样呢?看下面这张图就很容易理解了。

很显然,这个字符串的循环节长度为$2$。
**解释**:
设字串长度为 $x$,字符串从 $1$ 开始计数
$next[1]=next[2]=……next[x]=0$
$next[x+1]=1 next[x+n]=n$
发现从 $x+1$ 位置开始,$next$ 数组逐渐递增 $1$
所以答案为 $n-next[n]$
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1000010;
int n, ne[N];
char p[N];
int main() {
cin >> n >> (p + 1);
// 求模式串ne数组
for (int i = 2, j = 0; i <= n; i++) {
while (j && p[i] != p[j + 1]) j = ne[j];
if (p[i] == p[j + 1]) j++;
ne[i] = j;
}
printf("%d", n - ne[n]);
return 0;
}
```
### 八、参考资料
**[代码随想录的理论篇](https://www.bilibili.com/video/BV1PD4y1o7nd)**
**[代码随想录的代码篇](https://www.bilibili.com/video/BV1M5411j7Xx)**


