##[$AcWing$ $122$ 糖果传递](https://www.acwing.com/problem/content/description/124/)
### 一、题目描述
有 $n$ 个小朋友坐成一圈,每人有 $a[i]$ 个糖果。
**每人只能给左右两人传递糖果**。
每人每次传递一个糖果代价为 $1$。
**求使所有人获得均等糖果的最小代价**。
**输入格式**
第一行输入一个正整数 $n$,表示小朋友的个数。
接下来 $n$ 行,每行一个整数 $a[i]$,表示第 $i$ 个小朋友初始得到的糖果的颗数。
**输出格式**
输出一个整数,表示最小代价。
**数据范围**
$1≤n≤1000000,0≤a[i]≤2×10^9,$数据保证一定有解。
**输入样例:**
```cpp {.line-numbers}
4
1
2
5
4
```
**输出样例:**
```cpp {.line-numbers}
4
```
### 二、解题思路
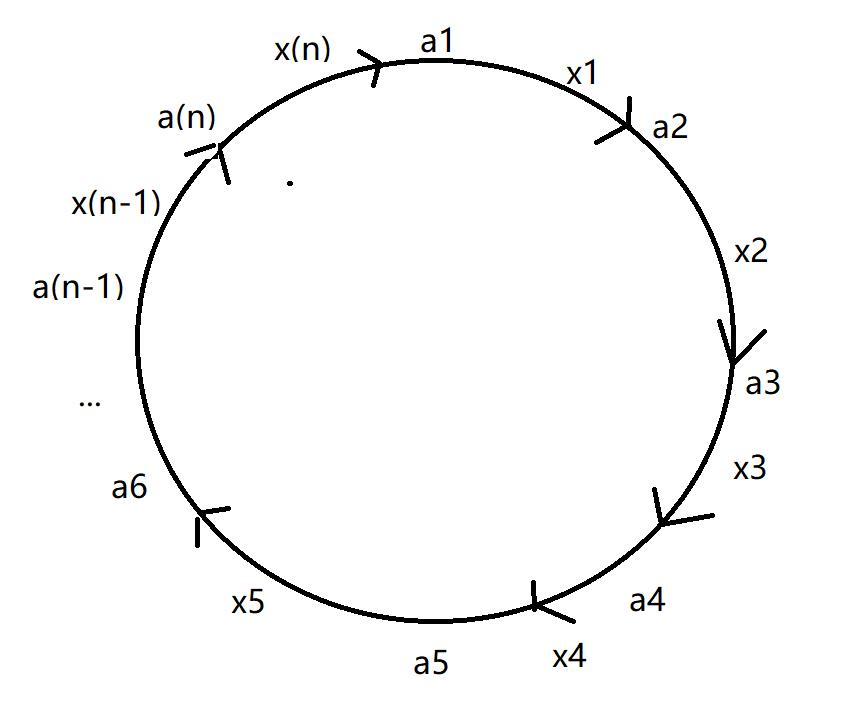 * 假设第$1$个小朋友有$a_1$颗糖果,给第$2$个小朋友$x_1$颗糖果,从$n$获得$x_n$颗糖果,此时,他有$a_1-x_1+x_n$颗糖果,同理,第$2$个有$a_2-x_2+x_1$,第$3$有...
* 每个小朋友的目标为平均数$avg$,列出约束方程为
$$\large \left\{\begin{matrix}
a_1-x_1+x_n=avg & \\
a_2-x_2+x_1=avg & \\
a_3-x_3+x_2=avg & \\
... \\
a_n-x_n+x_{n-1}=avg
\end{matrix}\right.
$$
我们的目标:
$$\large min(|x_1|+|x_2|+...+|x_n|)$$
下面,我们用$x_n$来表示上面的方程组:替代$x_1,x_2,...,x_{n-1}$
$$\large \left\{\begin{array}{l}
x_1=a_1+x_n-avg \\
x_2=a_2+x_1-avg =(a_1+a_2)-2*avg+x_n & \\
x_3=a_3+x_2-avg =(a_1+a_2+a_3)-3*avg+x_n & \\
... \\
x_{n-1}=(a_1+a_2+...+a_{n-1})-(n-1)*avg+x_n & \\
\end{array}\right.
$$
将$x_k$定为变量 , 常数 定义为$c_k$,则:
$$\large \displaystyle c_k=\sum_{i=1}^{k}a_i -k*avg$$
有:
$$\large \left\{\begin{array}{l}
x_1=c_1+x_n \\
x_2=c_2+x_n \\
... \\
x_{n-1}=c_{n-1}+x_n
\end{array}\right.
$$
因为$x_1,x_n$都是可正可负的,正的表示把这些糖果给了别人,负的表示别人把这些糖果给了自己。
所以,可以令$x_n'=-x_n$
上面的方程组转化为
$$\large \left\{\begin{array}{l}
x_1=c_1-x_n' \\
x_2=c_2-x_n' \\
... \\
x_{n-1}=c_{n-1}-x_n'
\end{array}\right.
$$
此时,我们的目标也就转化为:
$$\large min(|c_1-x_n'|+|c_2-x_n'|+...+|c_{n-1}-x_n'|)$$
**注意到** $|c_i-x_n'|$的几何意义是数轴上的点$c_i$到$x_n'$的距离,所以问题变成了:
> **给定数轴上的$n$个点,找出一个到他们的距离之和尽量小的点,而这个点就是这些数中的中位数,问题再次转化为经典问题:
**[$AcWing$ $104$.仓库选址](https://www.acwing.com/problem/content/106/)** ,只需要求中位数和其他数的差值的总和就可以了。**
### 三、实现代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1000010;
typedef long long LL;
LL a[N], c[N], sum, avg, n, res;
int main() {
// 加快读入
ios::sync_with_stdio(false), cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i], sum += a[i];
avg = sum / n;
// c[k]=(a[1]+a[2]+...+a[k])-k*avg
// c[k-1]=(a[1]+a[2]+...+a[k-1])-(k-1)*avg
// 努力找出c[k]与 c[k-1]之间的递推关系:
// c[k]=c[k-1]+a[k]-avg
// 所以,c数组可以通过递推得到
for (int k = 1; k <= n; k++) c[k] = c[k - 1] + a[k] - avg;
// 通过排序 => c[(n+1)/2] = 中位值
sort(c + 1, c + n + 1);
// 将x_n'放到中位值处,这样,几何含义上所有n 个位置上c1,c2,...cn到中位值的距离绝对值和最小
for (int i = 1; i <= n; i++) res += abs(c[i] - c[(n + 1) / 2]);
cout << res << endl;
return 0;
}
```
* 假设第$1$个小朋友有$a_1$颗糖果,给第$2$个小朋友$x_1$颗糖果,从$n$获得$x_n$颗糖果,此时,他有$a_1-x_1+x_n$颗糖果,同理,第$2$个有$a_2-x_2+x_1$,第$3$有...
* 每个小朋友的目标为平均数$avg$,列出约束方程为
$$\large \left\{\begin{matrix}
a_1-x_1+x_n=avg & \\
a_2-x_2+x_1=avg & \\
a_3-x_3+x_2=avg & \\
... \\
a_n-x_n+x_{n-1}=avg
\end{matrix}\right.
$$
我们的目标:
$$\large min(|x_1|+|x_2|+...+|x_n|)$$
下面,我们用$x_n$来表示上面的方程组:替代$x_1,x_2,...,x_{n-1}$
$$\large \left\{\begin{array}{l}
x_1=a_1+x_n-avg \\
x_2=a_2+x_1-avg =(a_1+a_2)-2*avg+x_n & \\
x_3=a_3+x_2-avg =(a_1+a_2+a_3)-3*avg+x_n & \\
... \\
x_{n-1}=(a_1+a_2+...+a_{n-1})-(n-1)*avg+x_n & \\
\end{array}\right.
$$
将$x_k$定为变量 , 常数 定义为$c_k$,则:
$$\large \displaystyle c_k=\sum_{i=1}^{k}a_i -k*avg$$
有:
$$\large \left\{\begin{array}{l}
x_1=c_1+x_n \\
x_2=c_2+x_n \\
... \\
x_{n-1}=c_{n-1}+x_n
\end{array}\right.
$$
因为$x_1,x_n$都是可正可负的,正的表示把这些糖果给了别人,负的表示别人把这些糖果给了自己。
所以,可以令$x_n'=-x_n$
上面的方程组转化为
$$\large \left\{\begin{array}{l}
x_1=c_1-x_n' \\
x_2=c_2-x_n' \\
... \\
x_{n-1}=c_{n-1}-x_n'
\end{array}\right.
$$
此时,我们的目标也就转化为:
$$\large min(|c_1-x_n'|+|c_2-x_n'|+...+|c_{n-1}-x_n'|)$$
**注意到** $|c_i-x_n'|$的几何意义是数轴上的点$c_i$到$x_n'$的距离,所以问题变成了:
> **给定数轴上的$n$个点,找出一个到他们的距离之和尽量小的点,而这个点就是这些数中的中位数,问题再次转化为经典问题:
**[$AcWing$ $104$.仓库选址](https://www.acwing.com/problem/content/106/)** ,只需要求中位数和其他数的差值的总和就可以了。**
### 三、实现代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1000010;
typedef long long LL;
LL a[N], c[N], sum, avg, n, res;
int main() {
// 加快读入
ios::sync_with_stdio(false), cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i], sum += a[i];
avg = sum / n;
// c[k]=(a[1]+a[2]+...+a[k])-k*avg
// c[k-1]=(a[1]+a[2]+...+a[k-1])-(k-1)*avg
// 努力找出c[k]与 c[k-1]之间的递推关系:
// c[k]=c[k-1]+a[k]-avg
// 所以,c数组可以通过递推得到
for (int k = 1; k <= n; k++) c[k] = c[k - 1] + a[k] - avg;
// 通过排序 => c[(n+1)/2] = 中位值
sort(c + 1, c + n + 1);
// 将x_n'放到中位值处,这样,几何含义上所有n 个位置上c1,c2,...cn到中位值的距离绝对值和最小
for (int i = 1; i <= n; i++) res += abs(c[i] - c[(n + 1) / 2]);
cout << res << endl;
return 0;
}
```
