##[$AcWing$ $107$. 超快速排序 ](https://www.acwing.com/problem/content/description/109/)

### 一、题目描述
在这个问题中，您必须分析特定的排序算法---- **超快速排序**。

该算法通过交换两个相邻的序列元素来处理 $n$ 个不同整数的序列，直到 **序列按升序排序**。

对于输入序列 `9 1 0 5 4`，超快速排序生成输出 `0 1 4 5 9`。

您的任务是确定超快速排序需要执行多少交换操作才能对给定的输入序列进行排序。

**输入格式**
输入包括一些测试用例。

每个测试用例的第一行输入整数 $n$，代表该用例中输入序列的长度。

接下来 $n$ 行每行输入一个整数 $a_i$,代表用例中输入序列的具体数据，第 $i$行的数据代表序列中第 $i$ 个数。

当输入用例中包含的输入序列长度为 $0$ 时，输入终止，该序列无需处理。

**输出格式**
对于每个需要处理的输入序列，输出一个整数 $op$，代表对给定输入序列进行排序所需的最小交换操作数，每个整数占一行。


**数据范围**
$0≤n<500000,$一个测试点中，所有 $n$ 的和不超过 $500000$。
$0≤a_i≤999999999$

**输入样例：**
```cpp {.line-numbers}
5
9
1
0
5
4
3
1
2
3
0
```
**输出样例：**
```cpp {.line-numbers}
6
0
```

### 二、解题思路
#### 引理：逆序数
在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个 **逆序**。一个排列中 **逆序的总数** 就称为这个排列的**逆序数**。

<font color='red' size=4><b>排列的逆序数等于该排列转化为自然排序（从小到大）的最小次数</b></font>

例如：$31425$ 的逆序数为$3$

* $3$无逆序，则$n_1 = 0$，

* $1$逆序有$3$，则$n_2 = 1$，

* $4$无逆序，则$n_3 = 0$，

* $2$逆序有$3,4$，则$n_4 = 2$，

* $5$无逆序，则$n_5 = 0$，

若将该序列转化成从小到大排序，需要$\large (n_1 + n_2 + n_3 + n_4 + n_5)=3$次交换。

> **黄海理解**：因为是一个个来观察的，所以，在来到当前数字面前时，前面的可以理解为已经调整好了顺序，支付了$n_i$的代价，这样就非常好理解了。

#### 直接计算
计算一个排列的逆序数的直接方法是逐个枚举逆序，同时统计个数。例如在序列 $\{3, 1, 4, 2, 5 \}$ 中，逆序依次为 $(3,1)，(3,2)，(4,3)$，因此该序列的逆序数为 $3$。

#### 归并排序
直接计数法虽然简单直观，但是其时间复杂度是$O(n^2)$。一个更快的计算方法是在 **归并排序** 的同时计算逆序数。且该方法只是交换相邻的两个元素，符合题意。

### 三、算法分析
#### 归并排序

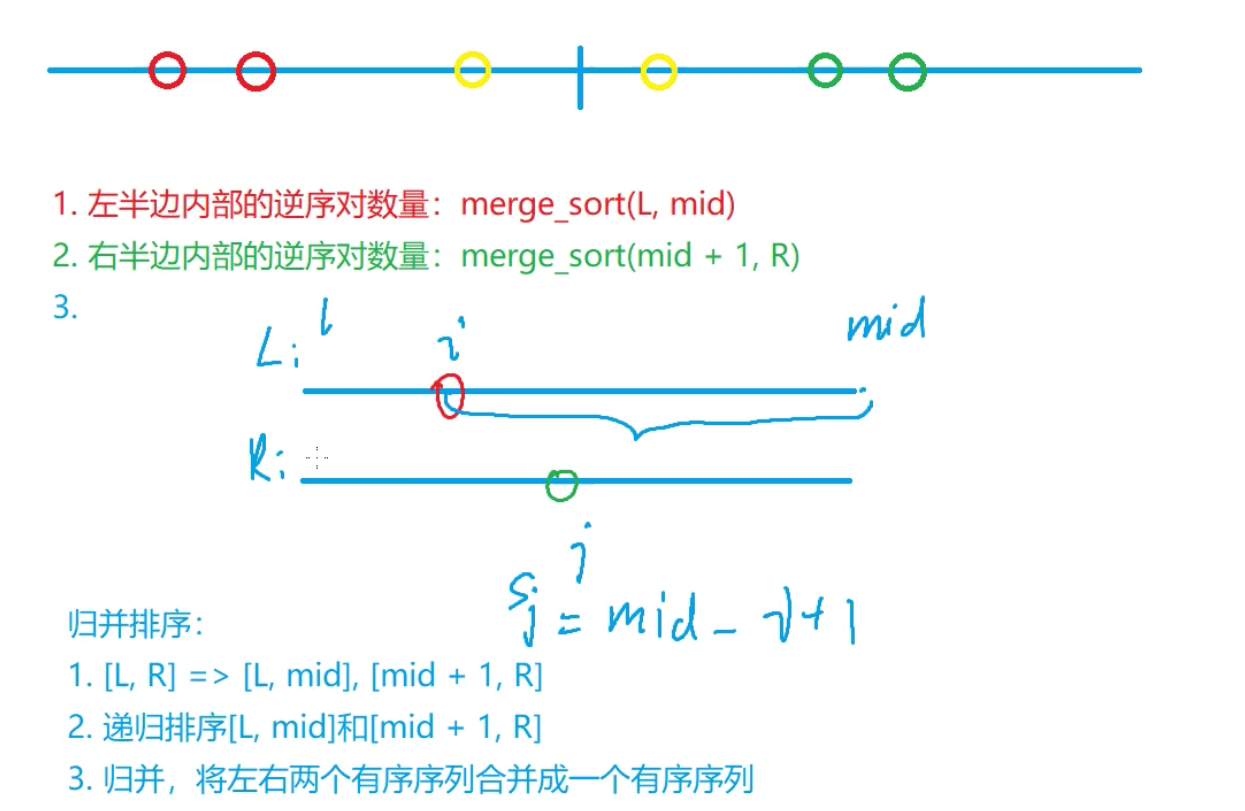
* 给定两个有序序列，从右边序列中最小的元素开始往左边序列中插入，设右边序列中选定的元素的位置为j，左边序列选定的元素位置为$i$，中间位置为$mid$，则此时交换的位置次数是$(mid - i + 1)$，最后把所有归并后交换的次数累加在一起即可。

* 例如 $31425$ 经过归并后得出两个有序序列 $134$ 和 $25$ （注意：$314$也是需要归并交换位置得到$123$的）即将$2$插入到$3$位置前，此操作相当于交换了两次位置，设$3$元素的位置为$i$，$4$元素的位置是中间位置$mid$，则此时交换的次数为$(mid - i + 1) = 2$次

#### 附上主播的图
<center><img src='https://cdn.acwing.com/media/article/image/2019/10/25/7416_8e3b27e4f6-ec8d32d62b62e7be74d4fe56db175a7.png'></center>


### 四、实现代码

```cpp {.line-numbers}
#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 500010;
int n;
LL q[N], t[N];
LL ans; // 结果

void merge_sort(LL q[], int l, int r) {
    if (l >= r) return;
    int mid = (l + r) >> 1;
    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);

    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r)
        if (q[i] <= q[j])
            t[k++] = q[i++];
        else {
            ans += mid - i + 1; // 如果q[i]>q[j],那么 i~mid之间所有数字，都>q[j]
            t[k++] = q[j++];
        }
    // 清理剩余
    while (i <= mid) t[k++] = q[i++];
    while (j <= r) t[k++] = q[j++];
    // 抄回来
    for (i = l, j = 0; i <= r; i++, j++) q[i] = t[j];
}

int main() {
    while (cin >> n, n) {
        for (int i = 1; i <= n; i++) cin >> q[i];
        ans = 0;
        merge_sort(q, 1, n);
        printf("%lld\n", ans);
    }
    return 0;
}
```