## [$AcWing$ $1077$. 皇宫看守](https://www.acwing.com/problem/content/1079/)
### 一、题目描述
太平王世子事件后,陆小凤成了皇上特聘的御前一品侍卫。
皇宫各个宫殿的分布,呈一棵树的形状,宫殿可视为树中节点,两个宫殿之间如果存在道路直接相连,则该道路视为树中的一条边。
已知,在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况,还能 **观察到与该宫殿直接存在道路相连的其他宫殿的状况**。
大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。
可是陆小凤手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。
帮助陆小凤布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
**输入格式**
输入中数据描述一棵树,描述如下:
第一行 $n$,表示树中节点的数目。
第二行至第 $n+1$ 行,每行描述每个宫殿节点信息,依次为:该宫殿节点标号 $i$,在该宫殿安置侍卫所需的经费 $k$,该节点的子节点数 $m$,接下来 $m$ 个数,分别是这个节点的 $m$ 个子节点的标号 $r_1,r_2,…,r_m$。
对于一个 $n$ 个节点的树,节点标号在 $1$ 到 $n$ 之间,且标号不重复。
**输出格式**
输出一个整数,表示最少的经费。
**数据范围**
$1≤n≤1500$
**输入样例:**
```cpp {.line-numbers}
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0
```
**输出样例:**
```cpp {.line-numbers}
25
```
**样例解释:**
在$2、3、4$节点安排护卫,可以观察到全部宫殿,所需经费最少,为 $16 + 5 + 4 = 25$。
### 二、对比
和 **[$Acwing$ $323$. 战略游戏](https://www.cnblogs.com/littlehb/p/15788291.html)** 这题非常类似,但又有些不同
$Acwing$ $323$. 战略游戏在一条道路的**两个节点至少有一个是放的**,而这题不一定,比如
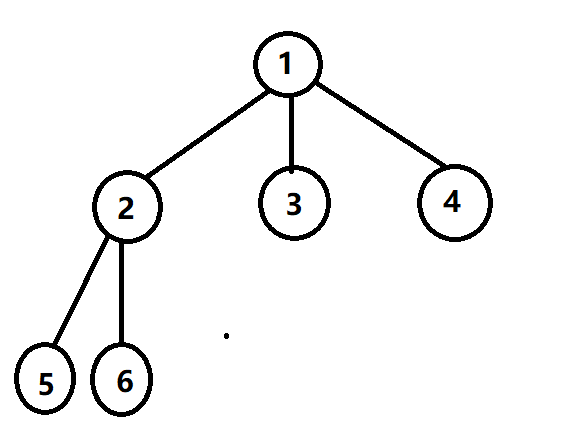 我们可以在$3$,$4$,$5$,$6$号点放,其他各点都不放。这样$1-2$的两个端点都没有守卫,这就和 **[$Acwing$ $323$. 战略游戏](https://www.cnblogs.com/littlehb/p/15788291.html)** 这题不同了
### 三、思路
不过稍微观察可以发现,**[$Acwing$ $323$. 战略游戏](https://www.cnblogs.com/littlehb/p/15788291.html)** 这题的 **切入点是边**,而本题的 **切入点是宫殿,也就是树上的节点**。那么可以用 **放不放** 这个状态上 **增加一个状态**,即
* 当前节点不放守卫
- 父节点放守卫:$f[u][0]$
- 子节点放守卫:$f[u][1]$
* 当前节点放置守卫:$f[u][2]$
其中$u$为当前节点,这样就可以 涵盖整个状态空间
> **解释**:状态描述这么划分,其实是 **存在重叠情况的**,比如$u$节点不放守卫,父节点放守卫:$f[u][0]$,而且,它的子节点也放了守卫:$f[u][1]$,这种情况是可能存在的:( $f[u][0]$与$f[u][1]$ 同时存在,不冲突!)。这样并不奇怪,因为我们最终要求的是最小值,只要不遗漏某种情况,最终的最小值是一样的
有了状态表示,接下来就是推导状态转移了,记$j$为$u$的子节点,那么
1. $\displaystyle \large f[u][0]=\sum min\left \{f[v][1],f[v][2] \right \}$
含义:当前节点$u$不放且被父节点看到,那么子节点$j$只能放或者被其子节点看到。
2. $\displaystyle \large f[u][1]=f[k][2]+ \sum min\left \{ f[v][1],f[v][2] \right \} ~ k \neq j$
含义:当前节点$u$不放,$u$的子节点$k$放了,$u$的其他子节点$j$放($f[j][2]$)或者不放(即$f[j][1]$),需要枚举$k$。
>没有$f[j][0]$是因为$u$不放
3. $\displaystyle \large f[u][2]=\sum min\left \{ f[v][0],f[v][1],f[v][2] \right \}$
含义:当前节点放了,那么子节点取哪种状态都可以
$1$,$3$实现起来比较容易,至于$2$的实现,有点麻烦,因为如果真的去一次次遍布计算是哪个$k$儿子,效率就会很低。
不这样算,还能怎么算呢?
#### 补集思想
- 把所有的$min(f[v][1],f[v][2])$都加在一起,不管$v$是不是等于$k$。
- 讨论自己不放守卫,枚举每个儿子视为好儿子,选中则$+f[v][2]$,同时,
其它儿子不靠父亲靠自己的代价总和就是 $sum(min(f[v][1],f[v][2]) - min(f[k][1],f[k][2])$,这样,算法就是$O(1)$的速度
### 四、树形$DP$代码
```cpp {.line-numbers}
#include
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 1510;
int n;
int h[N], e[N], ne[N], idx;
int w[N]; // 点的权值,不是边,不是边,不是边!
/*
状态表示:
(1)集合
f[u][0]:u号节点不放守卫,被父节点看守的方案
f[u][1]:u号节点不放守卫,被某个子节点看守的方案
f[u][2]:u号节点自己安排守卫看住的方案
(2)属性
花费最小值
*/
int f[N][3];
int in[N]; // 入度
// 邻接表
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u) {
// 初始化
f[u][0] = 0; // 被父亲守护,对于u子树而言,代价为0
f[u][1] = INF; // 被某个子节点守护,但还没有评选中由哪个来看守更合适,预求最小先设最大
f[u][2] = w[u]; // 被自己守护,对于u子树而言,代价为w[u]
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
dfs(j);
// ① u不放守卫,被父节点守护,它的儿子们可以放守卫,也可以不放守卫,两者代价取min
f[u][0] += min(f[j][1], f[j][2]);
// ③ u放守卫,儿子可以指望父亲,可以自己放守卫,也可以指望某个孙子来守卫,三者代价取min
f[u][2] += min({f[j][0], f[j][1], f[j][2]});
}
// ② u不放守卫,由某个好儿子守护
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
// Q:f[u][0]是什么意思?
// 向上看第39行,本质上就是所有子节点j的最小花费值累加和,没有扣除掉孝顺儿子的花费值
// 假设j是孝顺儿子,需要在其中扣除掉j的min(f[j][1],f[j][2])贡献,同时,
// 它的代价跑不了,此时就不能取min了,而是实打实的f[j][2]
f[u][1] = min(f[u][1], f[j][2] + f[u][0] - min(f[j][1], f[j][2]));
}
}
int main() {
memset(h, -1, sizeof h); // 初始化
cin >> n; // 节点数
for (int i = 1; i <= n; i++) { // n个节点
int x, m; // 节点号,代价,子节点数
cin >> x >> w[x] >> m;
while (m--) {
int y;
cin >> y;
add(x, y); // 有向图
in[y]++; // 入度,用于找根
}
}
// 找根
int root = 1;
while (in[root]) root++;
// dfs
dfs(root);
// f[root][0]表示root不放守卫,被父节点看守,根节点是没有父节点的, 所以此状态是无效状态,不参与结果讨论
// 最终最小代价值取min(f[root][1],f[root][2])
printf("%d\n", min(f[root][1], f[root][2]));
return 0;
}
```
### 五、问题与解答
#### $Q$:$f[u][1]$为什么要单独再开一个$for$来求,为什么不能直接在第一个$for$里面同时求$f[u][0]、f[u][2]$和$f[u][1]$?
答:
注意第一个循环中的写法:
```cpp {.line-numbers}
f[u][0] += min(f[v][1], f[v][2]);
```
这是在枚举每个`u`的儿子`v`,然后把`v`儿子自己放守卫,`v`儿子指望它的某个儿子看守望的情况两者的最小值进行累加,最终形成累加和$sum=f[u][0]$,注意,是最终的 **累加和** 啊!!!也就是所有儿子$v_1,v_2,v_3$,…的取值累加和。
在第二个循环中,我们期望如果现在指望 $v$儿子给$u$守卫的话,那么$f[v][2]$是肯定要付出的代价,那其它儿子需要付出的整体代价就是
$sum-min(f[v][1],f[v][2])$
注意:这里的是$sum$!!!
如果我们把三个状态转移全部放在第一个循环中,我们就会发现,当我们需要全部的累加和$sum$时,上面的$f[u][0]$还没有累加完毕!!还只是一部分儿子$v$的$sum$和,并不是全部,而我们要全部的$sum$和,这就意味着我们需要等待上面的所有$v$累加完,也就是执行完一遍循环后,才能拿到这个需要的$sum$值,这就解释了为什么要用两遍循环的原因。
我们可以在$3$,$4$,$5$,$6$号点放,其他各点都不放。这样$1-2$的两个端点都没有守卫,这就和 **[$Acwing$ $323$. 战略游戏](https://www.cnblogs.com/littlehb/p/15788291.html)** 这题不同了
### 三、思路
不过稍微观察可以发现,**[$Acwing$ $323$. 战略游戏](https://www.cnblogs.com/littlehb/p/15788291.html)** 这题的 **切入点是边**,而本题的 **切入点是宫殿,也就是树上的节点**。那么可以用 **放不放** 这个状态上 **增加一个状态**,即
* 当前节点不放守卫
- 父节点放守卫:$f[u][0]$
- 子节点放守卫:$f[u][1]$
* 当前节点放置守卫:$f[u][2]$
其中$u$为当前节点,这样就可以 涵盖整个状态空间
> **解释**:状态描述这么划分,其实是 **存在重叠情况的**,比如$u$节点不放守卫,父节点放守卫:$f[u][0]$,而且,它的子节点也放了守卫:$f[u][1]$,这种情况是可能存在的:( $f[u][0]$与$f[u][1]$ 同时存在,不冲突!)。这样并不奇怪,因为我们最终要求的是最小值,只要不遗漏某种情况,最终的最小值是一样的
有了状态表示,接下来就是推导状态转移了,记$j$为$u$的子节点,那么
1. $\displaystyle \large f[u][0]=\sum min\left \{f[v][1],f[v][2] \right \}$
含义:当前节点$u$不放且被父节点看到,那么子节点$j$只能放或者被其子节点看到。
2. $\displaystyle \large f[u][1]=f[k][2]+ \sum min\left \{ f[v][1],f[v][2] \right \} ~ k \neq j$
含义:当前节点$u$不放,$u$的子节点$k$放了,$u$的其他子节点$j$放($f[j][2]$)或者不放(即$f[j][1]$),需要枚举$k$。
>没有$f[j][0]$是因为$u$不放
3. $\displaystyle \large f[u][2]=\sum min\left \{ f[v][0],f[v][1],f[v][2] \right \}$
含义:当前节点放了,那么子节点取哪种状态都可以
$1$,$3$实现起来比较容易,至于$2$的实现,有点麻烦,因为如果真的去一次次遍布计算是哪个$k$儿子,效率就会很低。
不这样算,还能怎么算呢?
#### 补集思想
- 把所有的$min(f[v][1],f[v][2])$都加在一起,不管$v$是不是等于$k$。
- 讨论自己不放守卫,枚举每个儿子视为好儿子,选中则$+f[v][2]$,同时,
其它儿子不靠父亲靠自己的代价总和就是 $sum(min(f[v][1],f[v][2]) - min(f[k][1],f[k][2])$,这样,算法就是$O(1)$的速度
### 四、树形$DP$代码
```cpp {.line-numbers}
#include
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 1510;
int n;
int h[N], e[N], ne[N], idx;
int w[N]; // 点的权值,不是边,不是边,不是边!
/*
状态表示:
(1)集合
f[u][0]:u号节点不放守卫,被父节点看守的方案
f[u][1]:u号节点不放守卫,被某个子节点看守的方案
f[u][2]:u号节点自己安排守卫看住的方案
(2)属性
花费最小值
*/
int f[N][3];
int in[N]; // 入度
// 邻接表
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void dfs(int u) {
// 初始化
f[u][0] = 0; // 被父亲守护,对于u子树而言,代价为0
f[u][1] = INF; // 被某个子节点守护,但还没有评选中由哪个来看守更合适,预求最小先设最大
f[u][2] = w[u]; // 被自己守护,对于u子树而言,代价为w[u]
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
dfs(j);
// ① u不放守卫,被父节点守护,它的儿子们可以放守卫,也可以不放守卫,两者代价取min
f[u][0] += min(f[j][1], f[j][2]);
// ③ u放守卫,儿子可以指望父亲,可以自己放守卫,也可以指望某个孙子来守卫,三者代价取min
f[u][2] += min({f[j][0], f[j][1], f[j][2]});
}
// ② u不放守卫,由某个好儿子守护
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
// Q:f[u][0]是什么意思?
// 向上看第39行,本质上就是所有子节点j的最小花费值累加和,没有扣除掉孝顺儿子的花费值
// 假设j是孝顺儿子,需要在其中扣除掉j的min(f[j][1],f[j][2])贡献,同时,
// 它的代价跑不了,此时就不能取min了,而是实打实的f[j][2]
f[u][1] = min(f[u][1], f[j][2] + f[u][0] - min(f[j][1], f[j][2]));
}
}
int main() {
memset(h, -1, sizeof h); // 初始化
cin >> n; // 节点数
for (int i = 1; i <= n; i++) { // n个节点
int x, m; // 节点号,代价,子节点数
cin >> x >> w[x] >> m;
while (m--) {
int y;
cin >> y;
add(x, y); // 有向图
in[y]++; // 入度,用于找根
}
}
// 找根
int root = 1;
while (in[root]) root++;
// dfs
dfs(root);
// f[root][0]表示root不放守卫,被父节点看守,根节点是没有父节点的, 所以此状态是无效状态,不参与结果讨论
// 最终最小代价值取min(f[root][1],f[root][2])
printf("%d\n", min(f[root][1], f[root][2]));
return 0;
}
```
### 五、问题与解答
#### $Q$:$f[u][1]$为什么要单独再开一个$for$来求,为什么不能直接在第一个$for$里面同时求$f[u][0]、f[u][2]$和$f[u][1]$?
答:
注意第一个循环中的写法:
```cpp {.line-numbers}
f[u][0] += min(f[v][1], f[v][2]);
```
这是在枚举每个`u`的儿子`v`,然后把`v`儿子自己放守卫,`v`儿子指望它的某个儿子看守望的情况两者的最小值进行累加,最终形成累加和$sum=f[u][0]$,注意,是最终的 **累加和** 啊!!!也就是所有儿子$v_1,v_2,v_3$,…的取值累加和。
在第二个循环中,我们期望如果现在指望 $v$儿子给$u$守卫的话,那么$f[v][2]$是肯定要付出的代价,那其它儿子需要付出的整体代价就是
$sum-min(f[v][1],f[v][2])$
注意:这里的是$sum$!!!
如果我们把三个状态转移全部放在第一个循环中,我们就会发现,当我们需要全部的累加和$sum$时,上面的$f[u][0]$还没有累加完毕!!还只是一部分儿子$v$的$sum$和,并不是全部,而我们要全部的$sum$和,这就意味着我们需要等待上面的所有$v$累加完,也就是执行完一遍循环后,才能拿到这个需要的$sum$值,这就解释了为什么要用两遍循环的原因。

