##[$AcWing$ $3302$. 表达式求值](https://www.acwing.com/problem/content/description/3305/)
### 一、题目描述
给定一个表达式,其中运算符仅包含 `+,-,*,/`(加 减 乘 整除),可能包含括号,请你求出表达式的最终值。
**注意:**
- 数据保证给定的表达式合法。
- 题目保证符号 $-$只作为减号出现,不会作为负号出现,例如,$-1+2,(2+2)*(-(1+1)+2)$ 之类表达式均不会出现。
- 题目保证表达式中所有数字均为正整数。
- 题目保证表达式在中间计算过程以及结果中,均不超过 $2^{31}−1$。
- 题目中的整除是指向 $0$ 取整,也就是说对于大于 $0$ 的结果向下取整,例如 $5/3=1$
,对于小于 $0$ 的结果向上取整,例如 $5/(1−4)=−1$。
- $C++$和$Java$中的整除默认是向零取整;$Python$中的整除//默认向下取整,因此$Python$的$eval()$函数中的整除也是向下取整,在本题中不能直接使用。
**输入格式**
共一行,为给定表达式。
**输出格式**
共一行,为表达式的结果。
**数据范围**
表达式的长度不超过 $10^5$。
**输入样例:**
```cpp {.line-numbers}
(2+2)*(1+1)
```
**输出样例:**
```cpp {.line-numbers}
8
```
### 二、算法思路
同类题参考:
**[【$2013$ $NOIP$ 普及组】表达式求值](http://ybt.ssoier.cn:8088/problem_show.php?pid=1962)**
**[$CSP$ $2022$ $J2$ 试卷解析 第$3$题](https://www.cnblogs.com/littlehb/p/16865277.html)**
先看下只有 `+` 和 `*` 的。
输入长度为$n$的字符串,例如:$ 1 + 2 + 3 * 4 * 5$
输出表达式的值,即:$63$
**“表达式求值”问题,两个核心关键点:**
- 双栈,一个操作数栈,一个运算符栈;
- 运算符优先级:"栈顶运算符"与"即将入栈的运算符"的优先级比较:
* 如果栈顶的运算符优先级低,新运算符直接入栈。
* 如果栈顶的运算符优先级高,先出栈计算,新运算符再入栈。
**举个栗子**
$1+2+3 * 4 *5$,看是如何利用上述两个关键点实施计算的。
首先,这个例子只有`+`和`*`两个运算符,所以它的运算符表是:
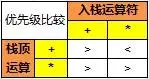 (1)如果栈顶是`+`,即将入栈的是`+`,栈顶优先级高,需要先计算,再入栈;
(2)如果栈顶是`+`,即将入栈的是`*`,栈顶优先级低,直接入栈;
(3)如果栈顶是`*`,即将入栈的是`+`,栈顶优先级高,需要先计算,再入栈;
(4)如果栈顶是`*`,即将入栈的是`*`,栈顶优先级高,需要先计算,再入栈;
有了运算符表,一切就好办了。
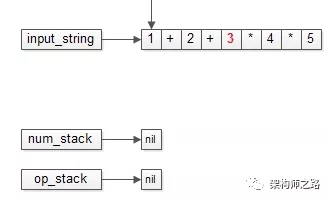
一开始,初始化好输入的字符串,以及操作数栈,运算符栈。
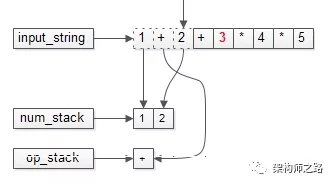
一步步,扫描字符串,操作数一个个入栈,运算符也入栈。
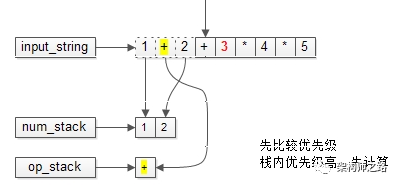
下一个操作符要入栈时,需要先比较优先级。
栈内的优先级高,必须先计算,才能入栈。
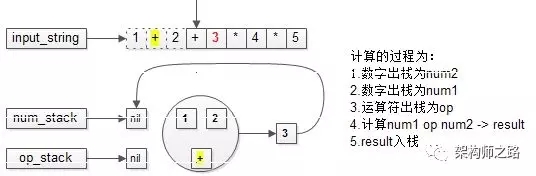
计算的过程为:
(1)操作数出栈,作为$num2$;
(2)操作数出栈,作为$num1$;
(3)运算符出栈,作为$op$;
(4)计算出结果;
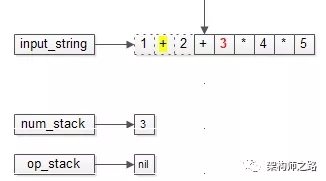
(5)结果入操作数栈;
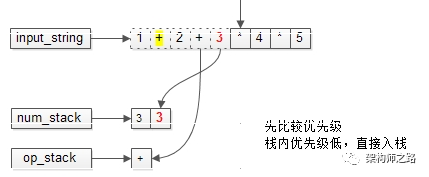
接下来,运算符和操作数才能继续入栈。下一个操作符要入栈时,继续比较与栈顶的优先级。
栈内的优先级低,可以直接入栈。
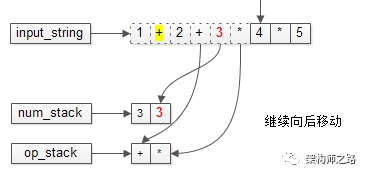
字符串继续移动。
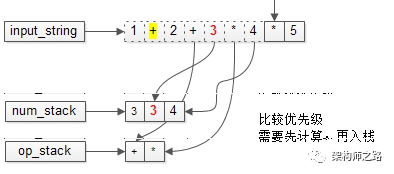
又要比较优先级了。
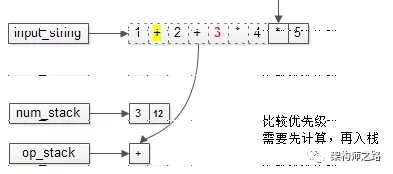
栈内的优先级高,还是先计算(`3*4=12`),再入栈。
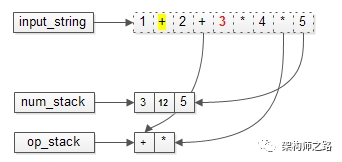
不断入栈,直到字符串扫描完毕。
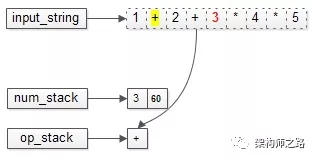
不断出栈,直到得到最终结果$3+60=63$,算法完成。
这个方法的时间复杂度为$O(n)$,整个字符串只需要扫描一遍。
运算符有$+$、 $-$、$*$、 $/$、 $($、 $)$、 $\{$ 、 $\}$ 都没问题,如果共有$n$个运算符,会有一个$n*n$的优先级表。
#### 小结
1. 运算符优先级表
2. 左括号直接入操作符栈,右括号不入操作符栈,看到右括号,就不断的处理操作符栈,直到看到左括号,再把左括号弹出。
3. 抽象出从一个字符串中读取数字的办法。
4. 抽象出两个数字通过数字栈、操作符栈进行计算的通用办法。
### 三、实现代码
```cpp {.line-numbers}
#include
using namespace std;
stack num; // 数字栈
stack op; // 操作符栈
// 优先级表
unordered_map h{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}, {'(', 0}};
/**
* 功能:计算两个数的和差积商
*/
void eval() {
int a = num.top(); // 第二个操作数
num.pop();
int b = num.top(); // 第一个操作数
num.pop();
char p = op.top(); // 运算符
op.pop();
int r; // 结果
// 计算结果
if (p == '+')
r = b + a;
else if (p == '-')
r = b - a;
else if (p == '*')
r = b * a;
else if (p == '/')
r = b / a;
// 结果入栈
num.push(r);
}
int main() {
// 读入表达式
string s;
cin >> s;
// 遍历字符串的每一位
for (int i = 0; i < s.size(); i++) {
// ① 如果是数字,则入栈
if (isdigit(s[i])) {
// 读出完整的数字
int x = 0;
while (i < s.size() && isdigit(s[i])) {
x = x * 10 + s[i] - '0';
i++;
}
i--; // 加多了一位,需要减去
num.push(x); // 数字入栈
}
// ② 左括号无优先级,入栈
else if (s[i] == '(')
op.push(s[i]);
// ③ 右括号时,需计算最近一对括号里面的值
else if (s[i] == ')') {
// 从栈中向前找,一直找到左括号
while (op.top() != '(') eval(); // 将左右括号之间的计算完,维护回栈里
// 左括号出栈
op.pop();
} else { // ④ 运算符
// 如果待入栈运算符优先级低,则先计算
while (op.size() && h[op.top()] >= h[s[i]]) eval();
op.push(s[i]); // 操作符入栈
}
}
while (op.size()) eval(); // ⑤ 剩余的进行计算
printf("%d\n", num.top()); // 输出结果
return 0;
}
```
(1)如果栈顶是`+`,即将入栈的是`+`,栈顶优先级高,需要先计算,再入栈;
(2)如果栈顶是`+`,即将入栈的是`*`,栈顶优先级低,直接入栈;
(3)如果栈顶是`*`,即将入栈的是`+`,栈顶优先级高,需要先计算,再入栈;
(4)如果栈顶是`*`,即将入栈的是`*`,栈顶优先级高,需要先计算,再入栈;
有了运算符表,一切就好办了。

一开始,初始化好输入的字符串,以及操作数栈,运算符栈。

一步步,扫描字符串,操作数一个个入栈,运算符也入栈。

下一个操作符要入栈时,需要先比较优先级。
栈内的优先级高,必须先计算,才能入栈。

计算的过程为:
(1)操作数出栈,作为$num2$;
(2)操作数出栈,作为$num1$;
(3)运算符出栈,作为$op$;
(4)计算出结果;

(5)结果入操作数栈;

接下来,运算符和操作数才能继续入栈。下一个操作符要入栈时,继续比较与栈顶的优先级。
栈内的优先级低,可以直接入栈。

字符串继续移动。

又要比较优先级了。

栈内的优先级高,还是先计算(`3*4=12`),再入栈。

不断入栈,直到字符串扫描完毕。

不断出栈,直到得到最终结果$3+60=63$,算法完成。
这个方法的时间复杂度为$O(n)$,整个字符串只需要扫描一遍。
运算符有$+$、 $-$、$*$、 $/$、 $($、 $)$、 $\{$ 、 $\}$ 都没问题,如果共有$n$个运算符,会有一个$n*n$的优先级表。
#### 小结
1. 运算符优先级表
2. 左括号直接入操作符栈,右括号不入操作符栈,看到右括号,就不断的处理操作符栈,直到看到左括号,再把左括号弹出。
3. 抽象出从一个字符串中读取数字的办法。
4. 抽象出两个数字通过数字栈、操作符栈进行计算的通用办法。
### 三、实现代码
```cpp {.line-numbers}
#include
using namespace std;
stack num; // 数字栈
stack op; // 操作符栈
// 优先级表
unordered_map h{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}, {'(', 0}};
/**
* 功能:计算两个数的和差积商
*/
void eval() {
int a = num.top(); // 第二个操作数
num.pop();
int b = num.top(); // 第一个操作数
num.pop();
char p = op.top(); // 运算符
op.pop();
int r; // 结果
// 计算结果
if (p == '+')
r = b + a;
else if (p == '-')
r = b - a;
else if (p == '*')
r = b * a;
else if (p == '/')
r = b / a;
// 结果入栈
num.push(r);
}
int main() {
// 读入表达式
string s;
cin >> s;
// 遍历字符串的每一位
for (int i = 0; i < s.size(); i++) {
// ① 如果是数字,则入栈
if (isdigit(s[i])) {
// 读出完整的数字
int x = 0;
while (i < s.size() && isdigit(s[i])) {
x = x * 10 + s[i] - '0';
i++;
}
i--; // 加多了一位,需要减去
num.push(x); // 数字入栈
}
// ② 左括号无优先级,入栈
else if (s[i] == '(')
op.push(s[i]);
// ③ 右括号时,需计算最近一对括号里面的值
else if (s[i] == ')') {
// 从栈中向前找,一直找到左括号
while (op.top() != '(') eval(); // 将左右括号之间的计算完,维护回栈里
// 左括号出栈
op.pop();
} else { // ④ 运算符
// 如果待入栈运算符优先级低,则先计算
while (op.size() && h[op.top()] >= h[s[i]]) eval();
op.push(s[i]); // 操作符入栈
}
}
while (op.size()) eval(); // ⑤ 剩余的进行计算
printf("%d\n", num.top()); // 输出结果
return 0;
}
```

