## [$AcWing$ $1069$. 凸多边形的划分 ](https://www.acwing.com/problem/content/1071/)
### 一、题目描述
给定一个具有 $N$ 个顶点的凸多边形,将顶点从 $1$ 至 $N$ 标号,每个顶点的权值都是一个正整数。
将这个凸多边形划分成 $N−2$ 个互不相交的三角形,对于每个三角形,其三个顶点的权值相乘都可得到一个权值乘积,**试求所有三角形的顶点权值乘积之和至少为多少**。
> 即:求所有三角形的顶点权值乘积之和的最小值
**输入格式**
第一行包含整数 $N$,表示顶点数量。
第二行包含 $N$ 个整数,依次为顶点 $1$ 至顶点 $N$ 的权值。
**输出格式**
输出仅一行,为所有三角形的顶点权值乘积之和的最小值。
**数据范围**
$N≤50$,数据保证所有顶点的权值都小于$10^9$
**输入样例**:
```cpp {.line-numbers}
5
121 122 123 245 231
```
**输出样例**:
```cpp {.line-numbers}
12214884
```
### 二、算法思路
这是一个经典的 **图形学** 问题 — **三角剖分**
因为我们现实中常见的一些 **多边形图形** 存储到计算机中,需要转存为一个个 **像素点**
那么如何存储一个 **多边形** 最简单的方案就是把它转化为 **多个三角形** 进行存储
也就是 **三角剖分** 问题,不只是 **凸多边形**,还能解决 **凹多边形**, **有孔多边形** 等问题
回归本题,本题是一个给定的 **凸多边形** 求 **三角剖分** 的 最小费用方案
#### 题意理解

看完题目描述后,我是一脸懵逼,不知道这是个啥意思。冷静下来看了下其它同学的题解,发现是以区间$DP$思路解决此问题,而区间是指任意两点$[l,r],(l结论:依题意,可以转化为求区间$[1,n]$之间所有可构成三角形的公式和最小值
很显然一个 **凸多边形的剖分方案** 并不唯一:
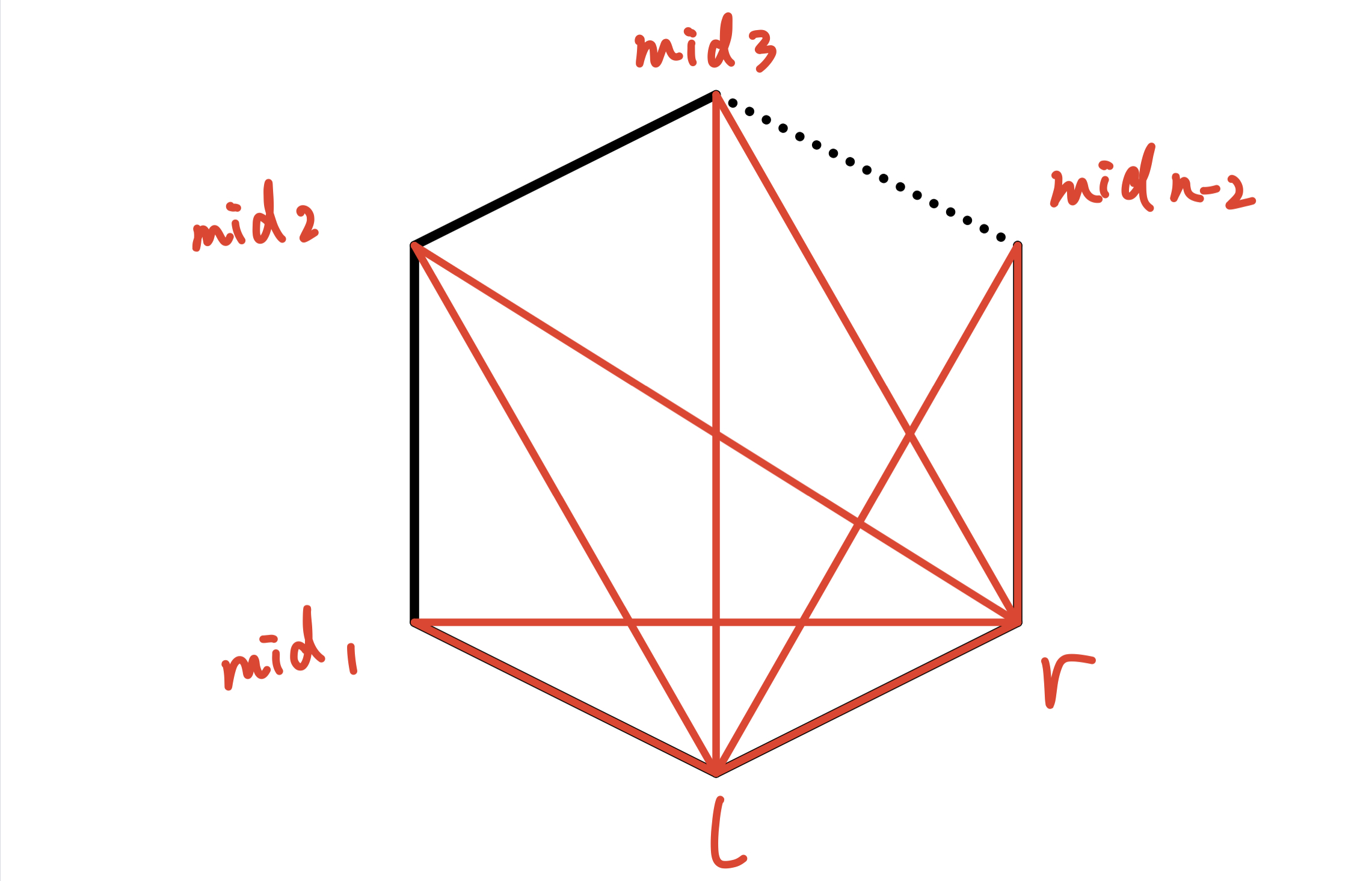 #### 闫氏$DP$分析法
**状态表示**—**集合**
$f[l][r]$:多边形的所有边【即:$(l,l+1),(1+1,l+2),...,(r-1,r),(l,r)$】划分成三角形的所有方案
**状态表示**—**属性**
$f[l][r]$:方案的最小费用
**状态计算**
>**其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少**。
所以代价是$\large w_l \times w_k \times w_j$,则状态转移方程:
$$\large f[l][r]=min(f[l][k]+f[k][r]+w_l×w_k×w_r)(l 允许使用以下划线开头的库函数或宏,但具有明确禁止操作的库函数和宏除外。
所以能在比赛中进行使用。
由于 $\_\_int128$ 仅仅是 ($GCC$) 编译器内的东西,不在 $(C++ 98/03/11/14/17/20)$ 标准内,
且仅 $(GCC4.6)$ 以上$64$位版本支持,很多配套都没有,只有四则运算功能。
目前$NOI$的$GCC$版本是$9.0$,放心使用~
[参考链接](https://www.bilibili.com/read/cv15945882)
[NOI Linux 2.0发布,将于9月1日起正式启用!](https://www.noi.cn/gynoi/jsgz/2021-07-16/732450.shtml)
#### 优点
$C++$内测的一种数据类型,$\_\_int128$的最大值是:
$\large ±85070591730234615865843651857942052864$,约为$\large 10^{38}$。
足够解决大部分高精度,大数据问题。
#### 缺点
* 手写输入输出
### 五、区间$DP+\_\_int128$作法
```cpp {.line-numbers}
#include
using namespace std;
const int N = 55;
typedef __int128 LL;
const LL INF = 1e38;
LL read() {
LL x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
void write(LL x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
LL f[N][N];
LL w[N];
int n;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) w[i] = read();
// 初始化
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
// 两个点之间最小差距是2,比如[1,3]这里面就有三角形,需要求解,如果小于2,比如[1,2]
// 无法构成三角形,就不需要求解,无法构成的情况贡献值是0,也是递推的起点,否则,全都是INF
// 就无法推起来了
j - i < 2 ? f[i][j] = 0 : f[i][j] = INF;
for (int len = 3; len <= n; len++) { // 区间范围最少是3个,否则无法构建三角形
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
for (int k = l + 1; k < r; k++) // l
using namespace std;
const int N = 50 + 10;
//__int128专用
typedef __int128 LL;
const LL INF = 1e38;
LL read() { // 快读
LL x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
void write(LL x) { // 快写
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
LL w[N];
LL f[N][N];
// 计算[l,r]之间的三角剖分最大值
LL dfs(int l, int r) {
LL &v = f[l][r];
if (v != INF) return v; // 记忆化
if (r - l < 2) return v = 0; // 不够三个点,哪来的剖分值
for (int k = l + 1; k < r; k++) // 中间点k不能与l,r重合
v = min(v, dfs(l, k) + dfs(k, r) + w[l] * w[r] * w[k]);
return v;
}
int main() {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) w[i] = read();
// 初始化极值
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
f[i][j] = INF;
write(dfs(1, n));
return 0;
}
```
### 七、高精度作法
```cpp {.line-numbers}
#include
using namespace std;
typedef long long LL;
const int N = 210;
const int M = 35;
const int INF = 0x3f3f3f3f;
int n;
LL f[N][N][M];
LL w[N];
// 判断a>b
bool cmp(LL a[], LL b[]) {
for (int i = M - 1; i >= 0; i--) { // 直接从高位进行比较,如果某一位a[i]>b[i],则说明a比b这个数大
if (a[i] > b[i]) return true;
if (a[i] < b[i]) return false;
}
return false;
}
// 直接从0位(个位)加,一直加到最高位M-1位
void add(LL a[], LL b[]) {
LL c[M] = {0}, t = 0;
for (int i = 0; i < M; i++) {
t += a[i] + b[i];
c[i] = t % 10;
t /= 10;
}
memcpy(a, c, sizeof c);
}
// 从0位(个位)开始乘,一直乘到最高位M-1位
void mul(LL a[], LL b) {
LL c[M] = {0}, t = 0;
for (int i = 0; i < M; i++) {
t += a[i] * b;
c[i] = t % 10;
t /= 10;
}
memcpy(a, c, sizeof c);
}
// 打印高精度结果数组
void print(LL a[]) {
int k = M - 1;
while (k && !a[k]) k--; // 输出之前要将所有的前导0都去掉
for (int i = k; i >= 0; i--) printf("%lld", a[i]);
puts("");
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &w[i]);
for (int len = 3; len <= n; len++) {
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
f[l][r][M - 1] = 1; // 因为高精度数组是高位在右,低位在左,这里设置的是最高位为1,目的是什么呢?
for (int k = l + 1; k < r; k++) { // 枚举中间点
LL t[M] = {0}; // 临时高精度数组
t[0] = 1; // 乘法的世界本原
mul(t, w[l]); // 高精度乘法
mul(t, w[k]); // 高精度乘法
mul(t, w[r]); // 高精度乘法
add(t, f[l][k]); // 高精度加法
add(t, f[k][r]); // 高精度加法
// 得到新的最大值,更新
if (cmp(f[l][r], t)) memcpy(f[l][r], t, sizeof t);
}
}
}
// 输出
print(f[1][n]);
return 0;
}
```
#### 闫氏$DP$分析法
**状态表示**—**集合**
$f[l][r]$:多边形的所有边【即:$(l,l+1),(1+1,l+2),...,(r-1,r),(l,r)$】划分成三角形的所有方案
**状态表示**—**属性**
$f[l][r]$:方案的最小费用
**状态计算**
>**其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少**。
所以代价是$\large w_l \times w_k \times w_j$,则状态转移方程:
$$\large f[l][r]=min(f[l][k]+f[k][r]+w_l×w_k×w_r)(l 允许使用以下划线开头的库函数或宏,但具有明确禁止操作的库函数和宏除外。
所以能在比赛中进行使用。
由于 $\_\_int128$ 仅仅是 ($GCC$) 编译器内的东西,不在 $(C++ 98/03/11/14/17/20)$ 标准内,
且仅 $(GCC4.6)$ 以上$64$位版本支持,很多配套都没有,只有四则运算功能。
目前$NOI$的$GCC$版本是$9.0$,放心使用~
[参考链接](https://www.bilibili.com/read/cv15945882)
[NOI Linux 2.0发布,将于9月1日起正式启用!](https://www.noi.cn/gynoi/jsgz/2021-07-16/732450.shtml)
#### 优点
$C++$内测的一种数据类型,$\_\_int128$的最大值是:
$\large ±85070591730234615865843651857942052864$,约为$\large 10^{38}$。
足够解决大部分高精度,大数据问题。
#### 缺点
* 手写输入输出
### 五、区间$DP+\_\_int128$作法
```cpp {.line-numbers}
#include
using namespace std;
const int N = 55;
typedef __int128 LL;
const LL INF = 1e38;
LL read() {
LL x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
void write(LL x) {
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
LL f[N][N];
LL w[N];
int n;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) w[i] = read();
// 初始化
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
// 两个点之间最小差距是2,比如[1,3]这里面就有三角形,需要求解,如果小于2,比如[1,2]
// 无法构成三角形,就不需要求解,无法构成的情况贡献值是0,也是递推的起点,否则,全都是INF
// 就无法推起来了
j - i < 2 ? f[i][j] = 0 : f[i][j] = INF;
for (int len = 3; len <= n; len++) { // 区间范围最少是3个,否则无法构建三角形
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
for (int k = l + 1; k < r; k++) // l
using namespace std;
const int N = 50 + 10;
//__int128专用
typedef __int128 LL;
const LL INF = 1e38;
LL read() { // 快读
LL x = 0, f = 1;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
void write(LL x) { // 快写
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + '0');
}
LL w[N];
LL f[N][N];
// 计算[l,r]之间的三角剖分最大值
LL dfs(int l, int r) {
LL &v = f[l][r];
if (v != INF) return v; // 记忆化
if (r - l < 2) return v = 0; // 不够三个点,哪来的剖分值
for (int k = l + 1; k < r; k++) // 中间点k不能与l,r重合
v = min(v, dfs(l, k) + dfs(k, r) + w[l] * w[r] * w[k]);
return v;
}
int main() {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) w[i] = read();
// 初始化极值
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
f[i][j] = INF;
write(dfs(1, n));
return 0;
}
```
### 七、高精度作法
```cpp {.line-numbers}
#include
using namespace std;
typedef long long LL;
const int N = 210;
const int M = 35;
const int INF = 0x3f3f3f3f;
int n;
LL f[N][N][M];
LL w[N];
// 判断a>b
bool cmp(LL a[], LL b[]) {
for (int i = M - 1; i >= 0; i--) { // 直接从高位进行比较,如果某一位a[i]>b[i],则说明a比b这个数大
if (a[i] > b[i]) return true;
if (a[i] < b[i]) return false;
}
return false;
}
// 直接从0位(个位)加,一直加到最高位M-1位
void add(LL a[], LL b[]) {
LL c[M] = {0}, t = 0;
for (int i = 0; i < M; i++) {
t += a[i] + b[i];
c[i] = t % 10;
t /= 10;
}
memcpy(a, c, sizeof c);
}
// 从0位(个位)开始乘,一直乘到最高位M-1位
void mul(LL a[], LL b) {
LL c[M] = {0}, t = 0;
for (int i = 0; i < M; i++) {
t += a[i] * b;
c[i] = t % 10;
t /= 10;
}
memcpy(a, c, sizeof c);
}
// 打印高精度结果数组
void print(LL a[]) {
int k = M - 1;
while (k && !a[k]) k--; // 输出之前要将所有的前导0都去掉
for (int i = k; i >= 0; i--) printf("%lld", a[i]);
puts("");
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &w[i]);
for (int len = 3; len <= n; len++) {
for (int l = 1; l + len - 1 <= n; l++) {
int r = l + len - 1;
f[l][r][M - 1] = 1; // 因为高精度数组是高位在右,低位在左,这里设置的是最高位为1,目的是什么呢?
for (int k = l + 1; k < r; k++) { // 枚举中间点
LL t[M] = {0}; // 临时高精度数组
t[0] = 1; // 乘法的世界本原
mul(t, w[l]); // 高精度乘法
mul(t, w[k]); // 高精度乘法
mul(t, w[r]); // 高精度乘法
add(t, f[l][k]); // 高精度加法
add(t, f[k][r]); // 高精度加法
// 得到新的最大值,更新
if (cmp(f[l][r], t)) memcpy(f[l][r], t, sizeof t);
}
}
}
// 输出
print(f[1][n]);
return 0;
}
``` #### 闫氏$DP$分析法
**状态表示**—**集合**
$f[l][r]$:多边形的所有边【即:$(l,l+1),(1+1,l+2),...,(r-1,r),(l,r)$】划分成三角形的所有方案
**状态表示**—**属性**
$f[l][r]$:方案的最小费用
**状态计算**
>**其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少**。
所以代价是$\large w_l \times w_k \times w_j$,则状态转移方程:
$$\large f[l][r]=min(f[l][k]+f[k][r]+w_l×w_k×w_r)(l
#### 闫氏$DP$分析法
**状态表示**—**集合**
$f[l][r]$:多边形的所有边【即:$(l,l+1),(1+1,l+2),...,(r-1,r),(l,r)$】划分成三角形的所有方案
**状态表示**—**属性**
$f[l][r]$:方案的最小费用
**状态计算**
>**其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少**。
所以代价是$\large w_l \times w_k \times w_j$,则状态转移方程:
$$\large f[l][r]=min(f[l][k]+f[k][r]+w_l×w_k×w_r)(l