## 分层图最短路

[P4568 [JLOI2011]飞行路线](https://www.luogu.org/problemnew/show/P4568)
### 一、分层图概念

**分层图最短路** :在可以进行分层图的图上解决最短路问题

**分层图**：理解为有 **多个平行的图**

**模型**：在一个正常的图上可以进行 $k$ 次决策，对于每次决策，不影响图的结构，只影响目前的 **状态** 或 **代价**。一般将 **决策前的状态** 和 **决策后的状态** 之间 **连接一条权值为决策代价的边**，表示付出该代价后就可以转换状态了


### 二、建图方式
有两种方法解决分层图最短路问题：

* 建图时 **直接建成$k+1$层**
* **多开一维** 记录分层信息


#### 1、建图时直接建成$k+1$层

我们建$k+1$层图。然后有边的两个点，多建一条到下一层边权为$0$的单向边，如果走了这条边就表示用了一次机会。

有$N$个点时:

<!-- 让表格居中显示的风格 -->
<style>
.center 
{
  width: auto;
  display: table;
  margin-left: auto;
  margin-right: auto;
}
</style>
<div class="center">

|  层数   | 开始  | 结束 |
|  ----  | ----  | ----  |
| 第一层  | $1$ | $n$ |
| 第二层  | $n+1$ |$2n$ |
| 第三层  | $2n+1$|$3n$|
| ...|  ...|...|
| 第$i$层| $(i-1)*n+1$|$i*n$|
| 第$i+1$层| $i*n+1$|$(i+1)*n$|
</div>

原始图要占一层，每经过一个条件变化，就到达一层，共$k$个条件，所以，要建$K+1$层图，数组要开到$n*(k+1)$，点的个数也为$n*(k+1)$ 

举个栗子：
```c++
n = 4，m = 3，k = 2

0  1  100
1  2  100
2  3  100
```
* $4$个节点，$3$条边，起点、终点、边权为上面的三组数据
* $2$有两条边可以免费，求第$3$长的边最短是多少

建成图之后大概是这样的：
![20221022112759](https://cdn.jsdelivr.net/gh/littlehb/ShaoHuiLin/20221022112759.png)  

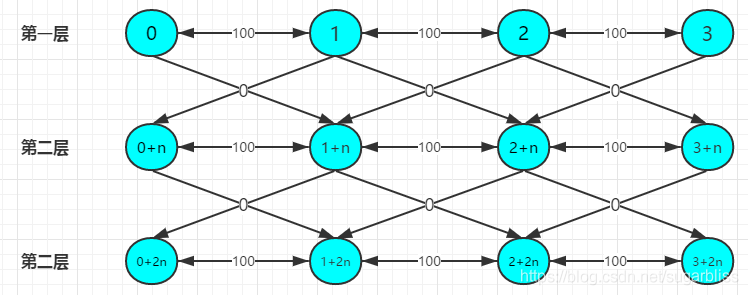
对于上面的数据：答案就是$3$，$3+n$，$3+2n$ 中的 **最小值**

**注意**
由于分层图的 **空间复杂度** 及 **时间复杂度较高**（特别是空间复杂度），故在分析时 **一定要计算好时间及空间**:

**边数**
*  $m*(k+1$)，无向图则需$*2$（可以理解为$2$个点互连的有向图）
*  考虑到每层图之间存在多条权值为$0$的边,一层最多有$m$条边，共$k+1$层(其实这里存在 **楼梯** 的是$k$层,多算一点防止$RE$)，考虑无向图，$*2$
$$\large M=m*(k+1)*2+m*(k+1)*2+10$$

本题就是：$M=5e4*11*2+ 5e4*11*2+ 10$

千万不要因为 **空间没开够** 或 **爆空间** 而导致$RE$！！！

```c++
#include <bits/stdc++.h>
using namespace std;

const int N = 1e4 * 2 * 11 + 10; //节点数：1e4,无向图，1e4*2,共k+1(k<=10)层:1e4*2*11
const int M = 5e4 * 11 * 3 + 10; //边数
typedef pair<int, int> PII;
const int INF = 0x3f3f3f3f;

int dist[N], st[N];

//邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int n, m, s, t, k;

void dijkstra() {
    priority_queue<PII, vector<PII>, greater<PII>> q;
    dist[s] = 0;
    q.push({0, s});

    while (q.size()) {
        int u = q.top().second;
        q.pop();

        if (st[u]) continue;
        st[u] = true;

        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (st[j]) continue;
            if (dist[j] > dist[u] + w[i]) {
                dist[j] = dist[u] + w[i];
                q.push({dist[j], j});
            }
        }
    }
}

int main() {
    //多组测试数据
    while (~scanf("%d%d%d", &n, &m, &k)) {
        //初始化
        memset(h, -1, sizeof(h));
        idx = 0;
        memset(dist, 0x3f, sizeof(dist));
        memset(st, false, sizeof(st));

        scanf("%d%d", &s, &t); //起点与终点

        while (m--) {
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            //分层图建图
            for (int i = 0; i <= k; i++) { //创建k+1层分层图
                add(a + i * n, b + i * n, c), add(b + i * n, a + i * n, c); //无向图
                if (i < k)                                                  //从第0层开始，到k-1层结束，都需要向下一层建立通道
                    add(a + i * n, b + (i + 1) * n, 0), add(b + i * n, a + (i + 1) * n, 0);
            }
        }
        //一遍最短路
        dijkstra();

        // k+1个层中，都去找t的最短路径，再取最小值，就是答案
        int ans = INF;
        for (int i = 0; i <= k; i++)
            ans = min(ans, dist[t + i * n]);

        printf("%d\n", ans);
    }
    return 0;
}
```

#### 2、多开一维记录分层信息
我们把$dist$数组和$st$数组 **多开一维** 记录$k$次机会的信息

$dist[i][j]$ 代表到达 $j$ 用了 $i$ 次免费机会的 **最小花费**

$st[i][j]$ 代表到达 $j$ 用了 $i$ 次 免费机会的情况 **是否出现过**

更新步骤： 
* **先更新同层之间**（即花费免费机会相同）的最短路

  `dist[r][j] = min(dist[r][j],dist[r][u] + w[i]);`

* **更新从该层到下一层**（即再花费一次免费机会）的最短路。
  `dist[r+1][j] = min(dist[r+1][j]，dist[r][u]);`

对于数据：
```c++
n = 4，m = 3，k = 2
0  1  100
1  2  100
2  3  100
```

建成图之后大概是这样的：
![20221022114046](https://cdn.jsdelivr.net/gh/littlehb/ShaoHuiLin/20221022114046.png)

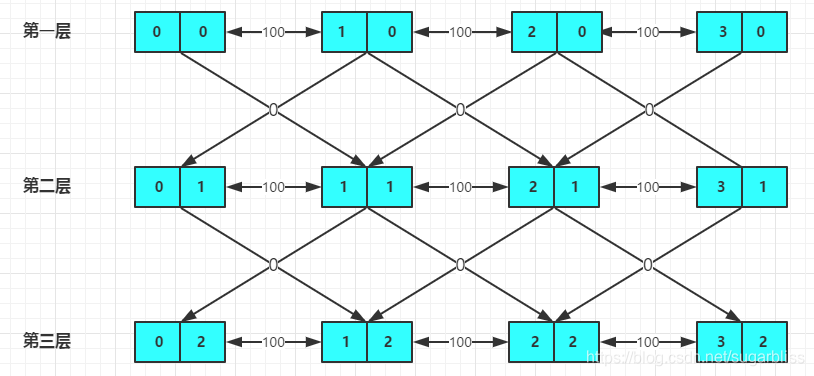
```c++
#include <bits/stdc++.h>
using namespace std;

const int INF = 0x3f3f3f3f;
typedef pair<int, int> PII;

const int N = 1e4 * 2 * 11 + 10; //节点数：1e4,无向图，1e4*2,共k+1(k<=10)层:1e4*2*11
const int M = N << 1;            //边数
//邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

int dist[15][N], st[15][N];
int n, m, s, t, k;

void dijkstra() {
    priority_queue<PII, vector<PII>, greater<PII>> q;
    dist[0][s] = 0; //第零层，起点s
    q.push({0, s});

    while (q.size()) {
        int u = q.top().second;
        q.pop();

        int r = u / n; //行
        u %= n;        //列
        if (st[r][u]) continue;
        st[r][u] = true;

        //更新同行,不使用免费机会
        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (st[r][j]) continue;
            if (dist[r][j] > dist[r][u] + w[i]) {
                dist[r][j] = dist[r][u] + w[i];
                q.push({dist[r][j], j + r * n});
            }
        }
        //更新下一行，使用免费机会
        if (r < k) {
            //出发点u,目标点：下一行的j位置
            for (int i = h[u]; ~i; i = ne[i]) {
                int j = e[i];
                if (st[r + 1][j]) continue;        //下一行，j列走过吗?
                if (dist[r + 1][j] > dist[r][u]) { //从r,u直接通过零成本过来 (r+1,j)
                    dist[r + 1][j] = dist[r][u];
                    q.push({dist[r + 1][j], j + (r + 1) * n});
                }
            }
        }
    }
}

int main() {
    while (~scanf("%d%d%d", &n, &m, &k)) {
        memset(h, -1, sizeof(h));
        memset(dist, 0x3f, sizeof(dist));
        memset(st, false, sizeof(st));
        idx = 0;

        scanf("%d%d", &s, &t);
        while (m--) {
            int a, b, c;
            scanf("%d%d%d", &a, &b, &c);
            add(a, b, c), add(b, a, c);
        }
        dijkstra();

        int ans = INF;
        for (int i = 0; i <= k; i++)
            ans = min(ans, dist[i][t]);
        printf("%d\n", ans);
    }
    return 0;
}
```

### 三、选择哪种方法 
具体选择哪一种方法，看数据范围吧:

* 直接建成$k+1$层
一次性建全$k+1$层，如果超过题目上限$128MB$，那么就只能使用第二种办法。


$$\large M=m*(k+1)*2+m*(k+1)*2 \approx m*4*k $$

比如本题：$m=5e4,k=10$，就是$5e4*4*10=2e6$

$2e6 *4byte=8e6 ~ byte = 7812kb = 7.6mb$

完全没有问题。


* 多开一维记录分层信息
这种办法由于只创建了一层节点的边关系，会小$k$倍的内存，同时，由于优先队列是一边进一边出的，所以内存可以控制。