poj 1830 开关问题
[题目传送门](http://poj.org/problem?id=1830)
### 1、描述
有一些开始状态的开关,题目让我们操控开关,使得开关从开始状态变成指定状态。
注意,当你操作一个开关,其关联的开关也会被操控。例如输入样例一,开始状态为$000$的三个开关,你要操作使其变成$111$。那么有以下四种方法:
* 只打开开关$1$,$2$ $and$ $3$和$1$关联,所以$2$ $and$ $3$也变成$1$
* 只打开开关$2$,$3$
* 只打开开关$3$,$4$
* 打开开关$1,2,3$
> 初始状态 $0$ $0$ $0$ $0$
终止状态 $1$ $1$ $1$ $1$
按下$i$号开关,会影响$j$号开关:
$1$ $3$
$3$ $1$
$3$ $4$
$4$ $1$
$4$ $3$
我能影响谁$a_i$
$a_1$->(1,0,1,0)->{$1$,$3$}
$a_2$->(0,1,0,0)->{$2$}
$a_3$->{$1,3,4$}
$a_4$->{$1,3,4$}
谁能影响我$k_i$
操作每个开关后,影响的情况
### 2、问题解决
我们用**线性方程组**来求解。
$$\large [a_1,a_2,a_3] * \begin{bmatrix}
x_1 \\
x_2 \\
x_3
\end{bmatrix} =b,即A_x=b
$$
由上图表达式,我们可以思考,倘若**乘号左边是开关的关联关系**,**乘号右边是开关操作**,那么两个矩阵相乘,**结果就是开关变化**。由此,我们可以让$b$为开关变化。
意思为当开关从$0$变为$1$,那么**开关有变化**,$b_i$为$1$;**当开关无变化**,则$b_i$为$0$。
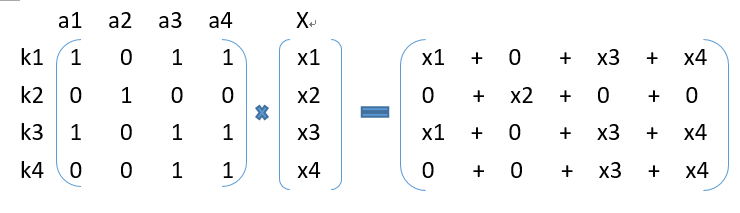 例如上面例子,$a_1=(1,0,1,0)$表示,操作开关$1$,开关$3$也会改变。即$a[i][j]$表示操作开关$j$,开关$i$也会变化。
所以,我们可以列出矩阵乘法表达式,然后进行高斯消元求解。
$Q$:为什么这里有反着记录的呢?
答:我们希望以方程组的形式对原问题进行求解。那么,由于有$n $盏灯,每个方程都要描述一盏灯的变化情况,这样的话,就共需要$n$个方程。
我们以第$1$盏灯为例,我们知道它的初始状态和终止状态,我们就可以研究它是在初始状态下,通过什么样的操作变化到终止状态的。因为灯开关的特殊性,关联一次就变化一次,所以,我们还可以取一巧:看看开始状态和终止状态是一样的呢,还是有了变化。
* 一样的
中间的变化是偶数次。用异或运算来描述就是异或和等于$0$。
* 不一样
中间的变化是奇数次。用异或运算来描述就是异或和等$1$。
**总结:我们关心的是状态的变化情况**
$1$号灯的变化,受和它相关联灯的制约,以上面的图为例说明:
第$1$盏灯的变化,受$1,3,4$三个灯的影响,我们可以把$1$盏灯的变化情况看作
$$\large 1*x_1+0*x_2+1*x_3+1*x_4$$
描述的说是:
* $1$号灯操作,影响$1$号灯的状态
* $2$号灯操作,不影响$1$号灯的状态
* $3$号灯操作,影响$1$号灯的状态
* $4$号灯操作,影响$1$号灯的状态
当然,只是说影响,但每个灯还有是权力决定自己是不是要操作的。
这就引出了一个系数的问题:
“**我是一号灯,谁能影响我的状态?**”
这玩意和题目中给的“**我是$x$号灯,我能影响$y$号灯**”是反着的,输入的时候要 小心识别 。
```c++
#include
#include
#include
#include
#include
例如上面例子,$a_1=(1,0,1,0)$表示,操作开关$1$,开关$3$也会改变。即$a[i][j]$表示操作开关$j$,开关$i$也会变化。
所以,我们可以列出矩阵乘法表达式,然后进行高斯消元求解。
$Q$:为什么这里有反着记录的呢?
答:我们希望以方程组的形式对原问题进行求解。那么,由于有$n $盏灯,每个方程都要描述一盏灯的变化情况,这样的话,就共需要$n$个方程。
我们以第$1$盏灯为例,我们知道它的初始状态和终止状态,我们就可以研究它是在初始状态下,通过什么样的操作变化到终止状态的。因为灯开关的特殊性,关联一次就变化一次,所以,我们还可以取一巧:看看开始状态和终止状态是一样的呢,还是有了变化。
* 一样的
中间的变化是偶数次。用异或运算来描述就是异或和等于$0$。
* 不一样
中间的变化是奇数次。用异或运算来描述就是异或和等$1$。
**总结:我们关心的是状态的变化情况**
$1$号灯的变化,受和它相关联灯的制约,以上面的图为例说明:
第$1$盏灯的变化,受$1,3,4$三个灯的影响,我们可以把$1$盏灯的变化情况看作
$$\large 1*x_1+0*x_2+1*x_3+1*x_4$$
描述的说是:
* $1$号灯操作,影响$1$号灯的状态
* $2$号灯操作,不影响$1$号灯的状态
* $3$号灯操作,影响$1$号灯的状态
* $4$号灯操作,影响$1$号灯的状态
当然,只是说影响,但每个灯还有是权力决定自己是不是要操作的。
这就引出了一个系数的问题:
“**我是一号灯,谁能影响我的状态?**”
这玩意和题目中给的“**我是$x$号灯,我能影响$y$号灯**”是反着的,输入的时候要 小心识别 。
```c++
#include
#include
#include
#include
#include 
