## [【算法学习】圆方树](https://www.cnblogs.com/PinkRabbit/p/Introduction-to-Block-Forest.html)
本知识点,涉及最大流,最小割等知识点,超出目前的通力范围,暂不研究,明年初开发学习进阶课,预计后年开始做周边习题。
写于 $2023-07-28$
众所周知,**树(或森林)有很好的性质**,并且容易通过很多常见数据结构维护。
而 **一般图** 则没有那么好的性质,所幸有时我们可以 **把一般图上的某些问题转化到树上考虑**。
而 **圆方树** 就是一种 **将图变成树** 的方法。本文将介绍圆方树的构建,性质和一些应用。
限于篇幅,本文中有一些结论未经证明,读者可以自行理解或证明。
### 一、圆方树的定义
圆方树最初是处理 **仙人掌图** (每条边在不超过一个简单环中的无向图)的一种工具,不过发掘它的更多性质,有时我们可以在一般无向图上使用它。
> **仙人掌图例子**
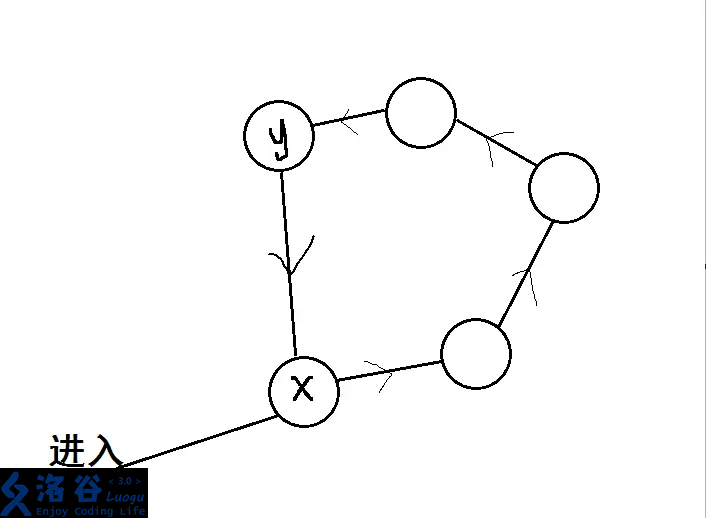
要介绍圆方树,首先要介绍 **点双连通分量**。
一个点双连通图的一个定义是:图中任意两不同点之间都有至少两条点不重复的路径。
点不重复既指路径上点不重复(简单路径),也指两条路径的交集为空(当然,路径必然都经过出发点和到达点,这不在考虑范围内)。
可以发现对于**只有一个点的图比较难定义它是不是一个点双,这里先不考虑节点数为 $1$ 的图**。
一个近乎等价的定义是:**不存在割点的图**。
这个定义只在图中只有两个点,一条连接它们的边时失效。它没有割点,但是并不能找到两条不相交的路径,因为只有一条路径。
(也可以理解为那一条路径可以算两次,的确没有交,因为不经过其他点)
虽然原始的定义的确是前者,但是为了方便,我们规定点双图的定义采用后者。
而一个图的点双连通分量则是一个极大点双连通子图。
与强连通分量等不同,一个点可能属于多个点双,但是一条边属于恰好一个点双(如果定义采用前者则有可能不属于任何点双)。
在圆方树中,原来的每个点对应一个圆点,每一个点双对应一个方点。
所以共有 $n+c$ 个点,其中 $n$ 是原图点数,$c$ 是原图点双连通分量的个数。
而对于每一个点双连通分量,它对应的方点向这个点双连通分量中的每个点连边。
每个点双形成一个 **菊花图** ,多个 **菊花图** 通过原图中的割点连接在一起(因为点双的分隔点是割点)。
显然,圆方树中每条边连接一个圆点和一个方点。
下面有一张图,来自 $WC$ 的 $PPT$,显示了一张图对应的点双和圆方树形态。
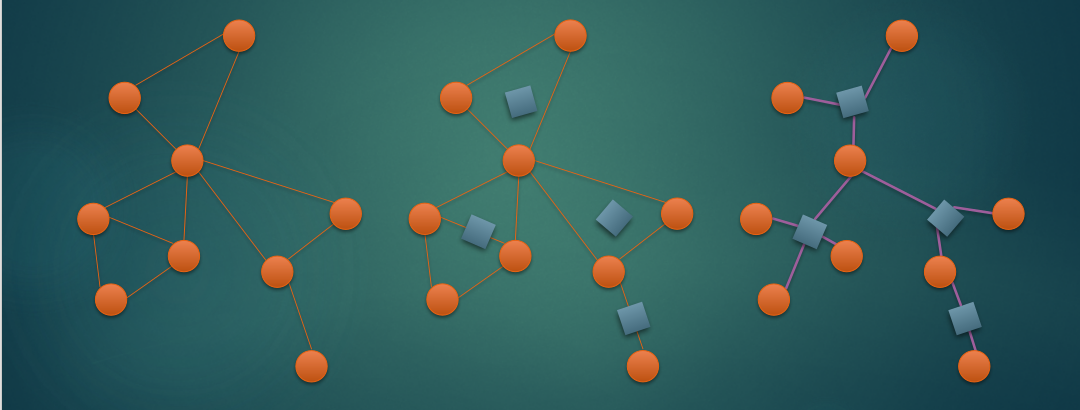
> **解释**: 原始无向连通图->划出点双->每个点双对应一个方点->抽象出这个方点->点双中所有点向这个点点连边->将无向图转化为圆方树
**圆方树的点数小于 $2n$,这是因为割点的数量小于 $n$,所以请注意各种数组大小要开两倍**。
其实,如果原图连通,则 **圆方树** 才是一棵树,如果原图有 $k$ 个连通分量,则它的圆方树也会形成 $k$ 棵树形成的森林。
> **注**:**如果原图中某个连通分量只有一个点,则需要具体情况具体分析,我们在后续讨论中不考虑孤立点**。
### 二、圆方树的构建
对于一个图,如何构造出它的圆方树呢?首先可以发现如果图不连通,可以拆分成每个连通子图考虑,所以我们只考虑连通图。
因为圆方树是基于点双连通分量的,而点双连通分量又基于割点,所以只需要用类似求割点的方法即可。
求割点的常用算法是 $Tarjan$ 算法,如果你会了理解下面的内容就很简单了,如果你不会也没关系。
我们跳过 $Tarjan$ 求割点,直接介绍圆方树使用的算法(其实是 $Tarjan$ 的变体):
对图进行 $DFS$,并且中间用到了两个关键数组 $dfn$ 和 $low$(类似于 $Tarjan$)。
- $dfn[u]$ 存储的是节点 $u$ 的 $DFS$ 序,即第一次访问到 $u$ 时它是第几个被访问的节点。
- $low[u]$ 存储的是节点 $u$ 的 $DFS$ 树中的子树中的某个点 $v$ 通过最多一次返祖边或向父亲的树边能访问到的点的最小 $DFS$ 序。
如果没有听说过 $Tarjan$ 算法可能会有点难理解,让我们举个例子吧:
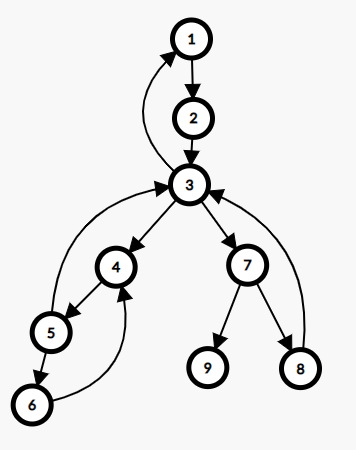
(可以发现这张图其实和上面图片中的图等价)
这里树边从上至下用直线画出,返祖边从下至上用曲线画出。节点的编号便是它的 $DFS$ 序。
则有 `low` 数组如下:

并不是很难理解吧,注意这里 $9$ 的 $low$ 是 $7$,与一些求割点的做法有差异,因为为了方便,我们规定了可以通过父边向上,但主要思想是相同的。
我们可以很容易地写出计算 $dfn$ 和 $low$ 的 $DFS$ 函数(初始时 $dfn$ 数组清零):
```cpp {.line-numbers}
void Tarjan(int u) {
low[u] = dfn[u] = ++dfc; // low 初始化为当前节点 dfn
for (int v : G[u]) { // 遍历 u 的相邻节点
if (!dfn[v]) { // 如果未访问过
Tarjan(v); // 递归
low[u] = min(low[u], low[v]); // 未访问的和 low 取 min
} else low[u] = min(low[u], dfn[v]); // 已访问的和 dfn 取 min
}
}
```
接下来,我们考虑点双和 $DFS$ 树以及这两个数组之间的关联。
可以发现,每个点双在 $DFS$ 树上是一棵连通子树,并至少包含两个点;特别地,最顶端节点仅往下接一个点。
同时还可以发现每条树边恰好在一个点双内。
我们考虑一个点双在 $DFS$ 树中的最顶端节点 $u$,在 $u$ 处确定这个点双,因为 $u$ 的子树包含了整个点双的信息。
因为至少有两个点,考虑这个点双的下一个点 $v$,则有 $u$,$v$ 之间存在一条树边。
不难发现,此时一定有 $low[v]=dfn[u]$。
更准确地说,对于一条树边 $u→v$,$u,v$ 在同一个点双中,且 $u$ 是这个点双中深度最浅的节点当且仅当 $low[v]=dfn[u]$。
这并不难处理,我们可以在 $DFS$ 过程中维护一个栈,存储还未确定所属点双(可能有多个)的节点。
在找到点双时,点双中除了 $u$ 以外的其他的点都集中在栈顶端,只需要不断弹栈直到弹出 $v$ 为止即可。
当然,我们可以同时处理被弹出的节点,只要将其和新建的方点连边即可。最后还要让 $u$ 和方点连边。
这样就很自然地完成了圆方树的构建,我们可以 **给方点标号为 $n+1$ 开始的整数,这样可以有效区分圆点和方点**。
这部分可能讲述得不够清晰,下面贴出一份代码,附有详尽注释以及帮助理解的输出语句和一份样例,**建议读者复制代码并自行实践理解,毕竟代码才是最能帮助理解的(不要忘记开 $c++11$)**。
```cpp {.line-numbers}
#include
#include
#include
using namespace std;
const int MN = 100005;
int N, M, cnt;
vector G[MN], T[MN * 2];
int dfn[MN], low[MN], dfc;
int stk[MN], tp;
void Tarjan(int u) {
printf(" Enter : #%d\n", u);
low[u] = dfn[u] = ++dfc; // low 初始化为当前节点 dfn
stk[++tp] = u; // 加入栈中
for (int v : G[u]) { // 遍历 u 的相邻节点
if (!dfn[v]) { // 如果未访问过
Tarjan(v); // 递归
low[u] = min(low[u], low[v]); // 未访问的和 low 取 min
if (low[v] == dfn[u]) { // 标志着找到一个以 u 为根的点双连通分量
++cnt; // 增加方点个数
printf(" Found a New BCC #%d.\n", cnt - N);
// 将点双中除了 u 的点退栈,并在圆方树中连边
for (int x = 0; x != v; --tp) {
x = stk[tp];
T[cnt].push_back(x);
T[x].push_back(cnt);
printf(" BCC #%d has vertex #%d\n", cnt - N, x);
}
// 注意 u 自身也要连边(但不退栈)
T[cnt].push_back(u);
T[u].push_back(cnt);
printf(" BCC #%d has vertex #%d\n", cnt - N, u);
}
} else
low[u] = min(low[u], dfn[v]); // 已访问的和 dfn 取 min
}
printf(" Exit : #%d : low = %d\n", u, low[u]);
printf(" Stack:\n ");
for (int i = 1; i <= tp; ++i) printf("%d, ", stk[i]);
puts("");
}
int main() {
#ifndef ONLINE_JUDGE
freopen("YFS.in", "r", stdin);
#endif
scanf("%d%d", &N, &M);
cnt = N; // 点双 / 方点标号从 N 开始
for (int i = 1; i <= M; ++i) {
int u, v;
scanf("%d%d", &u, &v);
G[u].push_back(v); // 加双向边,无向图
G[v].push_back(u);
}
// 处理非连通图
for (int u = 1; u <= N; ++u)
if (!dfn[u]) Tarjan(u), --tp;
// 注意到退出 Tarjan 时栈中还有一个元素即根,将其退栈
return 0;
}
```
> **注:黄海修改了一个使用链式前向星的版本,也是无向图,只有无向图中才有点双连通分量的概念**
```cpp {.line-numbers}
#include
using namespace std;
const int N = 1e5 + 10, M = N << 2;
int n, m;
int ts, root, dfn[N], low[N], stk[N], top;
vector bcc[N];
int bcc_cnt;
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c = 0) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
void tarjan(int u) {
printf(" Enter : #%d\n", u);
dfn[u] = low[u] = ++ts;
stk[++top] = u;
if (u == root && h[u] == -1) {
bcc[++bcc_cnt].push_back(u);
return;
}
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u]) {
bcc_cnt++;
printf(" Found a New BCC #%d.\n", bcc_cnt);
int bcc_id = bcc_cnt + n;
int x;
do {
x = stk[top--];
bcc[bcc_cnt].push_back(x);
// 将x向圆方树方格建边
add(x, bcc_id);
printf(" BCC #%d has vertex #%d\n", bcc_cnt, x);
} while (x != v);
bcc[bcc_cnt].push_back(u);
// 将u向圆方树方格建边
add(u, bcc_id);
printf(" BCC #%d has vertex #%d\n", bcc_cnt, u);
}
} else
low[u] = min(low[u], dfn[v]);
printf(" Exit : #%d : low = %d\n", u, low[u]);
printf(" Stack:\n ");
for (int i = 1; i <= top; ++i) printf("%d, ", stk[i]);
puts("");
}
}
int main() {
#ifndef ONLINE_JUDGE
freopen("YFS.in", "r", stdin);
freopen("YFS_2.out", "w", stdout);
#endif
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
add(a, b), add(b, a);
}
for (root = 1; root <= n; root++)
if (!dfn[root]) tarjan(root);
// for (int i = 1; i <= bcc_cnt; i++) {
// for (int j = 0; j < bcc[i].size(); j++)
// printf("%d ", bcc[i][j]);
// puts("");
// }
return 0;
}
```
提供一个测试用例:
```cpp {.line-numbers}
13 15
1 2
2 3
1 3
3 4
3 5
4 5
5 6
4 6
3 7
3 8
7 8
7 9
10 11
11 10
11 12
```
这个例子对应的图(包含了重边和孤立点的情况):
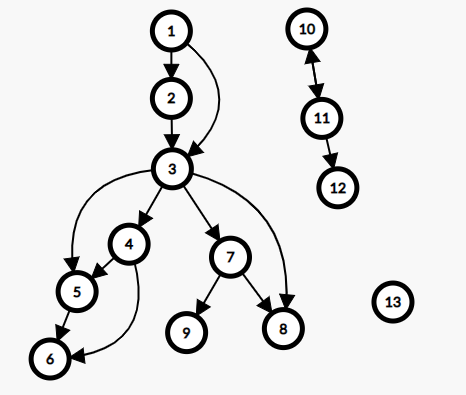
### 三、圆方树的应用
我们讲一些可以使用圆方树求解的例题。
#### [[APIO2018]铁人两项](https://loj.ac/p/2587)
这题可以作为圆方树模板题看待。