## [$AcWing$ $861$. 二分图的最大匹配](https://www.acwing.com/problem/content/863/)
### 一、题目描述
给定一个二分图,其中左半部包含 $n_1$ 个点(编号 $1∼n_1$),右半部包含 $n_2$ 个点(编号 $1∼n_2$),二分图共包含 $m$ 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数。
> 二分图的匹配:给定一个二分图 $G$,在 $G$ 的一个子图 $M$ 中,$M$ 的边集 ${E}$ 中的任意两条边都不依附于同一个顶点,则称 $M$ 是一个匹配。
>
二分图的最大匹配:所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
**输入格式**
第一行包含三个整数 $n_1$、 $n_2$ 和 $m$。
接下来 $m$ 行,每行包含两个整数 $u$ 和 $v$,表示左半部点集中的点 $u$ 和右半部点集中的点 $v$ 之间存在一条边。
**输出格式**
输出一个整数,表示二分图的最大匹配数。
**数据范围**
$1≤n1,n2≤500,1≤u≤n_1,1≤v≤n_2$,$1≤m≤10^5$
**输入样例:**
```cpp {.line-numbers}
2 2 4
1 1
1 2
2 1
2 2
```
**输出样例:**
```cpp {.line-numbers}
2
```
### 二、二分图的最大匹配
* 前提:给定一个二分图,不用你判断是不是二分图,已经明确知道是二分图,让你求它的最大匹配。
* 定义:在一个无向图中,定义一条边覆盖的点为这条边的两个端点。
找到一个边集$S$包含最多的边,使得这个边集覆盖到的所有顶点中的每个顶点只被一条边覆盖。$S$的大小叫做图的最大匹配。
#### 匈牙利算法
又名:【**月佬算法**】,目标:成就更多美满姻缘!
建立有向图$G$,分为二分图的左侧和右侧。 优先选择左侧序号更小的连接可能的边。 对于两个点的目标点“**冲突**”的时候,采取“**协商**”的办法。 即序号小的连接可能连接的另一条边。 若“**协商**”失败,则放弃序号较大的点的边。
概念看的都好绕,实例比较好懂:
你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
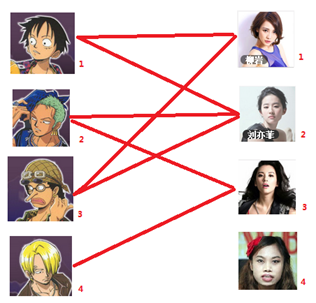 本着救人一命,胜造七级浮屠的原则,你想要尽可能地撮合更多的情侣,匈牙利算法的工作模式会教你这样做:
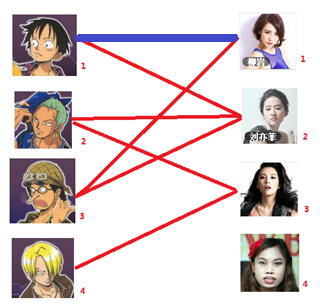
1. 先试着给$1$号男生找妹子,发现第一个和他相连的$1$号女生还名花无主,$got\ it$,连上一条蓝线
本着救人一命,胜造七级浮屠的原则,你想要尽可能地撮合更多的情侣,匈牙利算法的工作模式会教你这样做:
1. 先试着给$1$号男生找妹子,发现第一个和他相连的$1$号女生还名花无主,$got\ it$,连上一条蓝线
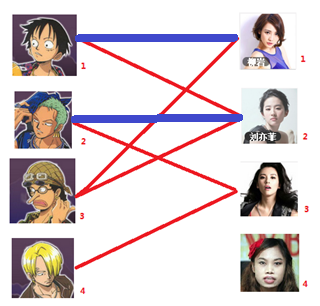
 2. 接着给$2$号男生找妹子,发现第一个和他相连的$2$号女生名花无主,$got\ it$
2. 接着给$2$号男生找妹子,发现第一个和他相连的$2$号女生名花无主,$got\ it$
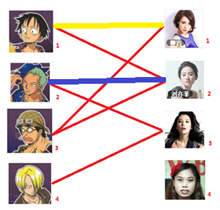
 3. 接下来是$3$号男生,很遗憾$1$号女生已经有主了,怎么办呢?
我们试着给之前$1$号女生匹配的男生(也就是$1$号男生)另外分配一个妹子。(黄色表示这条边被临时拆掉)
3. 接下来是$3$号男生,很遗憾$1$号女生已经有主了,怎么办呢?
我们试着给之前$1$号女生匹配的男生(也就是$1$号男生)另外分配一个妹子。(黄色表示这条边被临时拆掉)
 与$1$号男生相连的第二个女生是$2$号女生,但是$2$号女生也有主了,怎么办呢?我们再试着给$2$号女生的原配重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
与$1$号男生相连的第二个女生是$2$号女生,但是$2$号女生也有主了,怎么办呢?我们再试着给$2$号女生的原配重新找个妹子(注意这个步骤和上面是一样的,这是一个递归的过程)
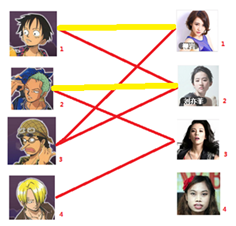 此时发现$2$号男生还能找到$3$号女生,那么之前的问题迎刃而解了,回溯回去
| $2$号男生可以找$3$号妹子 | $1$号男生可以找$2$号妹子 | $3$号男生可以找$1$号妹子 |
| ---------------------------------------------------------------------------------------------- | --------------------------------------------------------------------------------------------- | --------------------------------------------------------------------------------------------- |
|
此时发现$2$号男生还能找到$3$号女生,那么之前的问题迎刃而解了,回溯回去
| $2$号男生可以找$3$号妹子 | $1$号男生可以找$2$号妹子 | $3$号男生可以找$1$号妹子 |
| ---------------------------------------------------------------------------------------------- | --------------------------------------------------------------------------------------------- | --------------------------------------------------------------------------------------------- |
| 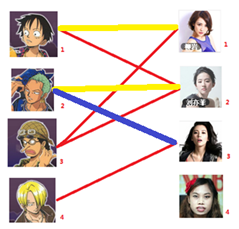 |
|  |
| 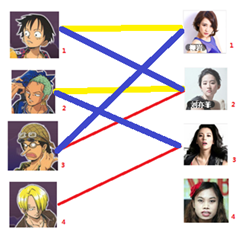 |
所以第3步最后的结果就是:
|
所以第3步最后的结果就是:
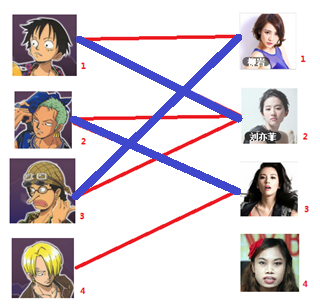 4. 接下来是$4$号男生,很遗憾,按照第三步的节奏我们没法给$4$号男生腾出来一个妹子,我们实在是无能为力了……香吉士同学走好。
### 三、实现代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 510;
const int M = 100010;
int n1, n2;
int m;
int match[N];
int st[N];
int res;
int h[N], e[M], ne[M], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dfs(int u) {
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!st[v]) {
st[v] = 1;
if (match[v] == 0 || dfs(match[v])) {
match[v] = u;
return 1;
}
}
}
return 0;
}
int main() {
memset(h, -1, sizeof h);
cin >> n1 >> n2 >> m;
while (m--) {
int a, b;
cin >> a >> b;
add(a, b);
}
for (int i = 1; i <= n1; i++) {
memset(st, 0, sizeof st);
if (dfs(i)) res++;
}
printf("%d\n", res);
return 0;
}
```
### 五、 解释`int st[N]`的作用
**重点**:`st[]`的作用:
首先我们$find(x)$ 遍历属于$h[x]$的单链表相当于遍历他所有喜欢的女生
如果某个女生$j$没有被他预定过的话,就标记这个女生$j$被他预定,即$st[j]=true$
这时如果女$j$还没有匹配过,即$match[j]==0$的时候,那这个预定就成真了,得到$match[j]=x$
而如果女$j$之前就被男$k$匹配过了,那我们就$find(k)$,也就是$find(match[j])$(因为原本$match[j]==k$)
然后在$find(k)$的过程中,因为$st[j]=true$,这时候男$k$就不能再选则女$j$了,因为女$j$已经被预定了,所以男$k$就只能在他喜欢的女生里面选择其他人来匹配。
当然,如果$find(k)$返回$false$的话,那就 $if(match[j]==0 || find(match[j]))$都不成立,那男$j$就一边玩去吧~
4. 接下来是$4$号男生,很遗憾,按照第三步的节奏我们没法给$4$号男生腾出来一个妹子,我们实在是无能为力了……香吉士同学走好。
### 三、实现代码
```cpp {.line-numbers}
#include
using namespace std;
const int N = 510;
const int M = 100010;
int n1, n2;
int m;
int match[N];
int st[N];
int res;
int h[N], e[M], ne[M], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dfs(int u) {
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!st[v]) {
st[v] = 1;
if (match[v] == 0 || dfs(match[v])) {
match[v] = u;
return 1;
}
}
}
return 0;
}
int main() {
memset(h, -1, sizeof h);
cin >> n1 >> n2 >> m;
while (m--) {
int a, b;
cin >> a >> b;
add(a, b);
}
for (int i = 1; i <= n1; i++) {
memset(st, 0, sizeof st);
if (dfs(i)) res++;
}
printf("%d\n", res);
return 0;
}
```
### 五、 解释`int st[N]`的作用
**重点**:`st[]`的作用:
首先我们$find(x)$ 遍历属于$h[x]$的单链表相当于遍历他所有喜欢的女生
如果某个女生$j$没有被他预定过的话,就标记这个女生$j$被他预定,即$st[j]=true$
这时如果女$j$还没有匹配过,即$match[j]==0$的时候,那这个预定就成真了,得到$match[j]=x$
而如果女$j$之前就被男$k$匹配过了,那我们就$find(k)$,也就是$find(match[j])$(因为原本$match[j]==k$)
然后在$find(k)$的过程中,因为$st[j]=true$,这时候男$k$就不能再选则女$j$了,因为女$j$已经被预定了,所以男$k$就只能在他喜欢的女生里面选择其他人来匹配。
当然,如果$find(k)$返回$false$的话,那就 $if(match[j]==0 || find(match[j]))$都不成立,那男$j$就一边玩去吧~






 |
|  |
|  |
所以第3步最后的结果就是:
|
所以第3步最后的结果就是:
