##[$AcWing$ $1282$. 搜索关键词](https://www.acwing.com/problem/content/1284/)
### 一、题目描述
给定 $n$ 个长度不超过 $50$ 的由小写英文字母组成的单词,以及一篇长为 $m$ 的文章。
请问,其中有多少个单词在文章中出现了。
**注意**:每个单词不论在文章中出现多少次,仅累计 $1$ 次。
**输入格式**
第一行包含整数 $T$,表示共有 $T$ 组测试数据。
对于每组数据,第一行一个整数 $n$,接下去 $n$ 行表示 $n$ 个单词,最后一行输入一个字符串,表示文章。
**输出格式**
对于每组数据,输出一个占一行的整数,表示有多少个单词在文章中出现。
**数据范围**
$1≤n≤10^4,1≤m≤10^6$
**输入样例**:
```cpp {.line-numbers}
1
5
she
he
say
shr
her
yasherhs
```
**输出样例**:
```cpp {.line-numbers}
3
```
### 二、$AC$自动机图解
#### 1、$AC$自动机与$kmp$的区别
| 算法 | 使用场景 |
| ---------- | ------------------ |
| $KMP$ | 单文本串,单模式串 |
| $AC$自动机 | 单文本串,多模式串 |
#### 2、推荐视频
[视频讲解](https://www.bilibili.com/video/BV1uJ411Y7Eg)
#### 3、算法步骤
$AC$自动机:在$Trie$树的基础上,增加一个 **失配** 时用的`fail`指针,如果当前点匹配失败,则将指针转移到`fail`指针指向的地方,这样就可以不用重头再来, **尽可能的利用已经知道的信息,能少退就少退** ,`fail` 指针的构建用 `bfs` 实现。
* ① 根据多个模式串建立$Trie$树
* ② 构建失配指针
* ③ 在构建的$AC$自动机上跑文本串
**举栗子说明**
 只需要 **遍历一遍文本串** 就 **找出所有单词表中存在的单词**:
先根据模式串集合{`she`,`he`,`say`,`shr`,`her`}建立$Trie$树,如图,然后拿着`yasherhs`去匹配:
- 发现前两个字符无法匹配,**跳过**
- 第三个字符开始,`she`可以匹配,**记录下来**,`ans++`,继续往后走发现没有匹配了,结果就是该文本串只存在一个单词`she`,很显然,**答案是错的**,因为存在`she`、`he`、`her`三个单词!
可以发现的是使用文本串在字典树上进行匹配的时候,**找到了一个单词结点后还应该看看有没有以该单词结点的后缀为 前缀 的其他单词**,比如`she`的后缀`he`是单词`he`和`her`的前缀。因此就需要一个 **失配指针** 在发现失配的时候指向其他存在`e`的结点,就通过`fail`指针的指引,跳到$root->he$这个位置,此时发现`e`有黄色标识,就是又找到一个模式串`he`,继续下一个字符,是$r$,发现后续可以匹配,匹配`her`了...
总的来说,$AC$自动机中失配指针和$KMP$中$ne$数组的作用是一致的,就是 **要想在只遍历一遍文本串的前提下,找到全部匹配模式串,就必须提前安排好匹配过程中失配后怎么办**。如果在在$Trie$树上构造 **失配指针** ,就是学习如何构造$AC$自动机。
#### 4、构建失配指针(构造$AC$自动机)
办法如下:
* 根结点的$ne$指针为空(或者它自己)
> **注释**:类比$kmp$,模式串的第一位,$ne[1]=0$,退无可退,无法再退
* 直接和根结点相连的结点,如果这些结点失配,就只能重新开始匹配,故它们的`ne`指针指向根结点
* 其它结点,设当前结点为`father`,其孩子结点为`child`。要寻找`child`的`ne`指针,需要看`father`的`ne`指针指向的结点,假设是`tmp`,要看`tmp`的孩子中有没有和`child`所代表的字符相同的,有则`child`的`ne`指针指向`tmp`的这个孩子结点,没有则继续沿着`tmp`的`ne`指针往上走,如果找到相同,就指向,如果一直找到了根结点的`ne`也就是空的时候,`child`的`ne`指针就指向`root`,表示重新从根结点开始匹配。
考察`father`的`ne`指针指向的结点有没有和`child`相同的结点,否则继续往上,就保证了前缀是相同的,比如刚才寻找右侧`h`的孩子结点`e`的`fail`指针时,找到右侧`h`的`fail`指针指向左侧的`h`结点,他的孩子中有`e`,就将右侧`h`的孩子`e`的`fail`指针指向它就保证了前缀`h`是相同的。
这样,就用`fail`指针来安排好每次失配后应该跳到哪里,而`fail`指针跳到哪里,说明从根结点到这个结点之前的字符串已经匹配过了,从而避免了重复匹配,也就解决了只遍历一次文本串就找出所有单词的问题。
#### 5、匹配过程
匹配就很简单了,这里以 `ashw` 为例:
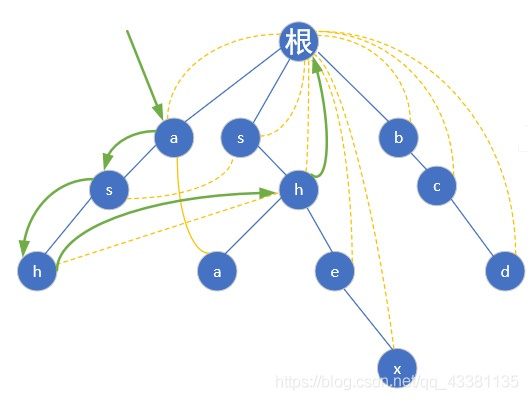
先用 `ash` 匹配,到 `h` 了发现,`ash` 是一个完整的模式串,则$ans++$,然后找下一个 `w`,可是 `ash` 后面没字母了呀,我们就跳到 `h` 的 $fail$ 指针指向的那个 `h` 继续找,还是没有 ? 再跳,结果当前的 `h` 指向的是根节点,又从根节点找,然而还是没有找到 `w`,匹配结束(假设如果有`w`的话,那么模式串`shw`就可以匹配上`ashw`)。流程图如下:
只需要 **遍历一遍文本串** 就 **找出所有单词表中存在的单词**:
先根据模式串集合{`she`,`he`,`say`,`shr`,`her`}建立$Trie$树,如图,然后拿着`yasherhs`去匹配:
- 发现前两个字符无法匹配,**跳过**
- 第三个字符开始,`she`可以匹配,**记录下来**,`ans++`,继续往后走发现没有匹配了,结果就是该文本串只存在一个单词`she`,很显然,**答案是错的**,因为存在`she`、`he`、`her`三个单词!
可以发现的是使用文本串在字典树上进行匹配的时候,**找到了一个单词结点后还应该看看有没有以该单词结点的后缀为 前缀 的其他单词**,比如`she`的后缀`he`是单词`he`和`her`的前缀。因此就需要一个 **失配指针** 在发现失配的时候指向其他存在`e`的结点,就通过`fail`指针的指引,跳到$root->he$这个位置,此时发现`e`有黄色标识,就是又找到一个模式串`he`,继续下一个字符,是$r$,发现后续可以匹配,匹配`her`了...
总的来说,$AC$自动机中失配指针和$KMP$中$ne$数组的作用是一致的,就是 **要想在只遍历一遍文本串的前提下,找到全部匹配模式串,就必须提前安排好匹配过程中失配后怎么办**。如果在在$Trie$树上构造 **失配指针** ,就是学习如何构造$AC$自动机。
#### 4、构建失配指针(构造$AC$自动机)
办法如下:
* 根结点的$ne$指针为空(或者它自己)
> **注释**:类比$kmp$,模式串的第一位,$ne[1]=0$,退无可退,无法再退
* 直接和根结点相连的结点,如果这些结点失配,就只能重新开始匹配,故它们的`ne`指针指向根结点
* 其它结点,设当前结点为`father`,其孩子结点为`child`。要寻找`child`的`ne`指针,需要看`father`的`ne`指针指向的结点,假设是`tmp`,要看`tmp`的孩子中有没有和`child`所代表的字符相同的,有则`child`的`ne`指针指向`tmp`的这个孩子结点,没有则继续沿着`tmp`的`ne`指针往上走,如果找到相同,就指向,如果一直找到了根结点的`ne`也就是空的时候,`child`的`ne`指针就指向`root`,表示重新从根结点开始匹配。
考察`father`的`ne`指针指向的结点有没有和`child`相同的结点,否则继续往上,就保证了前缀是相同的,比如刚才寻找右侧`h`的孩子结点`e`的`fail`指针时,找到右侧`h`的`fail`指针指向左侧的`h`结点,他的孩子中有`e`,就将右侧`h`的孩子`e`的`fail`指针指向它就保证了前缀`h`是相同的。
这样,就用`fail`指针来安排好每次失配后应该跳到哪里,而`fail`指针跳到哪里,说明从根结点到这个结点之前的字符串已经匹配过了,从而避免了重复匹配,也就解决了只遍历一次文本串就找出所有单词的问题。
#### 5、匹配过程
匹配就很简单了,这里以 `ashw` 为例:
先用 `ash` 匹配,到 `h` 了发现,`ash` 是一个完整的模式串,则$ans++$,然后找下一个 `w`,可是 `ash` 后面没字母了呀,我们就跳到 `h` 的 $fail$ 指针指向的那个 `h` 继续找,还是没有 ? 再跳,结果当前的 `h` 指向的是根节点,又从根节点找,然而还是没有找到 `w`,匹配结束(假设如果有`w`的话,那么模式串`shw`就可以匹配上`ashw`)。流程图如下:
 ### 三、朴素版本【不推荐,学习用】
```cpp {.line-numbers}
#include
using namespace std;
const int N = 55 * 1e4 + 10; // n个单词
const int M = 1e6 + 10; // 长度为m的文章
int n;
int tr[N][26], cnt[N], idx; // Trie树,每个结点的结束标识数组cnt,结点号计数器idx,二维代表最多可能有26条不同走向的边
char s[M]; // 字符串数组
int q[N], ne[N]; // AC自动机构建需要的队列和失配指针
// Trie树构建
void insert(char *s) {
int p = 0;
for (int i = 0; s[i]; i++) {
int t = s[i] - 'a';
if (!tr[p][t]) tr[p][t] = ++idx;
p = tr[p][t];
}
cnt[p]++;
}
// 构建AC自动机
void build() {
int hh = 0, tt = -1;
// 树根和树根下一层的失配边都连到树根上,所以从树根下一层开始bfs
for (int i = 0; i < 26; i++)
if (tr[0][i]) q[++tt] = tr[0][i];
while (hh <= tt) {
int t = q[hh++];
for (int i = 0; i < 26; i++) { // u节点有哪些出边
int p = tr[t][i]; // v是 u通过i这条边到达的子节点
if (!p) continue; // 如果v并不存在,就直接返回
int j = ne[t]; // u的失配指针指向了j
while (j && !tr[j][i]) j = ne[j]; // p需要它父亲u的失配指针j=ne[t]出发,一直跳到有i这条边为止,当然,也可能跳到了根也找不到i这条边
if (tr[j][i]) ne[p] = tr[j][i]; // 如果最终的停止节点j,有i这条边,则进入tr[j][i]这个点,这个点就是节点v失配后的指向节点。当然,ne[j]也可能跳回了根
// 填充儿子节点v的失配指针为它父亲给找的最佳匹配j
q[++tt] = p; // 将节点v放入队列
}
}
}
int query(char *s) {
int res = 0;
int j = 0; // 从root=0开始对AC自动机进行查找
for (int i = 0; s[i]; i++) {
int t = s[i] - 'a';
while (j && !tr[j][t]) j = ne[j]; // 一直跳到有t这条边的节点处或者跳到root停止
if (tr[j][t]) j = tr[j][t];
// 累加计数
int p = j;
while (p && ~cnt[p]) {
res += cnt[p];
cnt[p] = -1; // 取消标识
p = ne[p];
}
}
return res;
}
int main() {
int T;
cin >> T;
while (T--) {
memset(tr, 0, sizeof tr);
memset(cnt, 0, sizeof cnt);
memset(ne, 0, sizeof ne);
idx = 0;
// Trie树
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> s;
insert(s);
}
// ac自动机
build();
// 查询
cin >> s;
printf("%d\n", query(s));
}
return 0;
}
```
其实,这是一个不断回溯的过程,在代码实现时,我们采用的是$while$循环或者递归来不断的向上进行查找,但这样效率上会差一些。有没有更好的办法呢?这得益于我们采用的$bfs$策略,我们通过**自顶向下**的覆盖方式,将上面的信息继承到下面去,换句话说,就是不用儿子去找父亲问,父亲再找爷爷问,这太麻烦了,而且爷爷将答案准备好,告诉父亲,父亲将答案保存好,儿子可以直接获取到。这时就不再是一个$Trie$树了,而是一个$Trie$图了,类似于并查集的路径压缩~
### 四、$Trie$图优化版本【需背诵】
```cpp {.line-numbers}
#include
using namespace std;
const int N = 55 * 1e4 + 10;
const int M = 1e6 + 10;
int n;
int tr[N][26], cnt[N], idx;
char s[M];
int q[N], ne[N];
// 标准的Trie树构建
void insert(char *s) {
int p = 0;
for (int i = 0; s[i]; i++) {
int t = s[i] - 'a';
if (!tr[p][t]) tr[p][t] = ++idx;
p = tr[p][t];
}
cnt[p]++;
}
// 构建失配指针
void bfs() {
int hh = 0, tt = -1;
for (int i = 0; i < 26; i++)
if (tr[0][i]) q[++tt] = tr[0][i];
while (hh <= tt) {
int p = q[hh++];
for (int i = 0; i < 26; i++) {
int &c = tr[p][i]; // p:父节点,c:子节点,&:引用,可以向c赋值,等同于向tr[p][i]赋值
if (c) { // 如果点c存在
ne[c] = tr[ne[p]][i]; // 为点c填充失配数组ne,当点c失配时,跳到它父亲记录好的tr[ne[p]][i]位置上去,而它的父亲对应值,是记录了祖先传递下来的,不用再回溯求递归求解
q[++tt] = c; // 入队列,为后续填充做准备
} else
c = tr[ne[p]][i]; // 如果不存在,这个位置需要不需进行记录值呢?如果不用的话,那么后面再有指望它来提供信息的,就狒狒了,既然要递推,就要保证数据的完整
// 那怎么办呢?答案就是也依赖于它的真系血亲进行数据传递,说白了,就是自己这不匹配了,那么需要去哪里匹配呢?还不想用while向上递归,那就需要向下传递时记录清楚呗。
// 这个真系血亲是和c点拥有最长公共前后缀的节点,跳到它那里去
}
}
// ① 遍历完第i-1层时,会求出第i层节点的ne值(可不一定都在i-1层啊);也就是说遍历到第i层的时候第i层的ne值已知。
}
// 跑一下文本串
int query(char *s) {
int res = 0;
int j = 0; // 在Trie中游走的指针j, 从根开始对AC自动机进行查找
for (int i = 0; s[i]; i++) { // 枚举文本串每个字符
int t = s[i] - 'a'; // 字符映射的边序号
while (j && !tr[j][t]) j = ne[j]; // 如果没有回退到根,并且,当前游标位置没有t这条边,继续利用失配指针回退
if (tr[j][t]) j = tr[j][t]; // 如果命中,停下来,找到匹配的失配节点
// 统计在当前失配节点向根游走,有多少个完整的模式串被命中
int p = j;
while (p && ~cnt[p]) {
res += cnt[p]; // 记录个数
cnt[p] = -1; // 取消标识,一个模式串就算命中多次,也计数为1。测试用例中有重复的模式串,所以cnt[p]可能大于1
p = ne[p]; // 不断向上回退
}
}
return res;
}
int main() {
int T;
cin >> T;
while (T--) {
// 多组测试数组,初始化AC自动机
memset(tr, 0, sizeof tr);
memset(cnt, 0, sizeof cnt);
memset(ne, 0, sizeof ne);
idx = 0;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> s;
insert(s); // 构造Trie树
}
// 利用bfs构建Trie树的fail指针,也就是AC自动机
bfs();
// 输入文本串开始进行查询
cin >> s;
printf("%d\n", query(s));
}
return 0;
}
```
### 五、$Q$:为什么没有边时也需要进行赋值呢,我看原始版本没有这样的代码啊?
**答**:其实$AC$自动机就是一个$Trie+Fail$数组构建的过程,$bfs$由上到下去构建,还想不用$while$循环防止每次都向上查询,就想着从上到下时把信息都填充完整,这样下面用时就不用担心了,(线性$DP$的思路啊~),也就是在第$i$个节点填充$ne[i]$时,它前面的$i-1$都得是已经填充完整的状态,否则无法实现转移。
那如果现在$p$不存在,那就啥不做的话,如果后续节点中有问它这个问题,想找是不是以$p$出发有边$i$时,它可以说没有,人家问那我继续找谁问啊,他说我也不知道,供应链条就断开了,这肯定不行。
那怎么办呢?还得在由上到下的填充过程中想办法,使得就算是不存在的位置,也需要需要退回到哪里去!
退到哪里去呢?就是从当前的视角看,就是退回到离它最近的血缘关系最近的那个节点,也就是有最长公共前后缀的节点吧~,我只能转给它来回答,至它有没有知道不知道,那是它的问题!这是采用的办法就是 李代桃僵!直接将此位置的节点号写成上面血亲的号吧!有人问时,直接就不找我了,直接找它了,呵呵,爽!但它血亲也是这么想的,也可能没有i这条边,所以,它也是抄的上面传递过的值,这样,一个抄一个,问到不知道的,其实就直接没经过它走到了它上$N$级血亲有$i$边的节点上去了,当然,也可能跳到了根。
### 三、朴素版本【不推荐,学习用】
```cpp {.line-numbers}
#include
using namespace std;
const int N = 55 * 1e4 + 10; // n个单词
const int M = 1e6 + 10; // 长度为m的文章
int n;
int tr[N][26], cnt[N], idx; // Trie树,每个结点的结束标识数组cnt,结点号计数器idx,二维代表最多可能有26条不同走向的边
char s[M]; // 字符串数组
int q[N], ne[N]; // AC自动机构建需要的队列和失配指针
// Trie树构建
void insert(char *s) {
int p = 0;
for (int i = 0; s[i]; i++) {
int t = s[i] - 'a';
if (!tr[p][t]) tr[p][t] = ++idx;
p = tr[p][t];
}
cnt[p]++;
}
// 构建AC自动机
void build() {
int hh = 0, tt = -1;
// 树根和树根下一层的失配边都连到树根上,所以从树根下一层开始bfs
for (int i = 0; i < 26; i++)
if (tr[0][i]) q[++tt] = tr[0][i];
while (hh <= tt) {
int t = q[hh++];
for (int i = 0; i < 26; i++) { // u节点有哪些出边
int p = tr[t][i]; // v是 u通过i这条边到达的子节点
if (!p) continue; // 如果v并不存在,就直接返回
int j = ne[t]; // u的失配指针指向了j
while (j && !tr[j][i]) j = ne[j]; // p需要它父亲u的失配指针j=ne[t]出发,一直跳到有i这条边为止,当然,也可能跳到了根也找不到i这条边
if (tr[j][i]) ne[p] = tr[j][i]; // 如果最终的停止节点j,有i这条边,则进入tr[j][i]这个点,这个点就是节点v失配后的指向节点。当然,ne[j]也可能跳回了根
// 填充儿子节点v的失配指针为它父亲给找的最佳匹配j
q[++tt] = p; // 将节点v放入队列
}
}
}
int query(char *s) {
int res = 0;
int j = 0; // 从root=0开始对AC自动机进行查找
for (int i = 0; s[i]; i++) {
int t = s[i] - 'a';
while (j && !tr[j][t]) j = ne[j]; // 一直跳到有t这条边的节点处或者跳到root停止
if (tr[j][t]) j = tr[j][t];
// 累加计数
int p = j;
while (p && ~cnt[p]) {
res += cnt[p];
cnt[p] = -1; // 取消标识
p = ne[p];
}
}
return res;
}
int main() {
int T;
cin >> T;
while (T--) {
memset(tr, 0, sizeof tr);
memset(cnt, 0, sizeof cnt);
memset(ne, 0, sizeof ne);
idx = 0;
// Trie树
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> s;
insert(s);
}
// ac自动机
build();
// 查询
cin >> s;
printf("%d\n", query(s));
}
return 0;
}
```
其实,这是一个不断回溯的过程,在代码实现时,我们采用的是$while$循环或者递归来不断的向上进行查找,但这样效率上会差一些。有没有更好的办法呢?这得益于我们采用的$bfs$策略,我们通过**自顶向下**的覆盖方式,将上面的信息继承到下面去,换句话说,就是不用儿子去找父亲问,父亲再找爷爷问,这太麻烦了,而且爷爷将答案准备好,告诉父亲,父亲将答案保存好,儿子可以直接获取到。这时就不再是一个$Trie$树了,而是一个$Trie$图了,类似于并查集的路径压缩~
### 四、$Trie$图优化版本【需背诵】
```cpp {.line-numbers}
#include
using namespace std;
const int N = 55 * 1e4 + 10;
const int M = 1e6 + 10;
int n;
int tr[N][26], cnt[N], idx;
char s[M];
int q[N], ne[N];
// 标准的Trie树构建
void insert(char *s) {
int p = 0;
for (int i = 0; s[i]; i++) {
int t = s[i] - 'a';
if (!tr[p][t]) tr[p][t] = ++idx;
p = tr[p][t];
}
cnt[p]++;
}
// 构建失配指针
void bfs() {
int hh = 0, tt = -1;
for (int i = 0; i < 26; i++)
if (tr[0][i]) q[++tt] = tr[0][i];
while (hh <= tt) {
int p = q[hh++];
for (int i = 0; i < 26; i++) {
int &c = tr[p][i]; // p:父节点,c:子节点,&:引用,可以向c赋值,等同于向tr[p][i]赋值
if (c) { // 如果点c存在
ne[c] = tr[ne[p]][i]; // 为点c填充失配数组ne,当点c失配时,跳到它父亲记录好的tr[ne[p]][i]位置上去,而它的父亲对应值,是记录了祖先传递下来的,不用再回溯求递归求解
q[++tt] = c; // 入队列,为后续填充做准备
} else
c = tr[ne[p]][i]; // 如果不存在,这个位置需要不需进行记录值呢?如果不用的话,那么后面再有指望它来提供信息的,就狒狒了,既然要递推,就要保证数据的完整
// 那怎么办呢?答案就是也依赖于它的真系血亲进行数据传递,说白了,就是自己这不匹配了,那么需要去哪里匹配呢?还不想用while向上递归,那就需要向下传递时记录清楚呗。
// 这个真系血亲是和c点拥有最长公共前后缀的节点,跳到它那里去
}
}
// ① 遍历完第i-1层时,会求出第i层节点的ne值(可不一定都在i-1层啊);也就是说遍历到第i层的时候第i层的ne值已知。
}
// 跑一下文本串
int query(char *s) {
int res = 0;
int j = 0; // 在Trie中游走的指针j, 从根开始对AC自动机进行查找
for (int i = 0; s[i]; i++) { // 枚举文本串每个字符
int t = s[i] - 'a'; // 字符映射的边序号
while (j && !tr[j][t]) j = ne[j]; // 如果没有回退到根,并且,当前游标位置没有t这条边,继续利用失配指针回退
if (tr[j][t]) j = tr[j][t]; // 如果命中,停下来,找到匹配的失配节点
// 统计在当前失配节点向根游走,有多少个完整的模式串被命中
int p = j;
while (p && ~cnt[p]) {
res += cnt[p]; // 记录个数
cnt[p] = -1; // 取消标识,一个模式串就算命中多次,也计数为1。测试用例中有重复的模式串,所以cnt[p]可能大于1
p = ne[p]; // 不断向上回退
}
}
return res;
}
int main() {
int T;
cin >> T;
while (T--) {
// 多组测试数组,初始化AC自动机
memset(tr, 0, sizeof tr);
memset(cnt, 0, sizeof cnt);
memset(ne, 0, sizeof ne);
idx = 0;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> s;
insert(s); // 构造Trie树
}
// 利用bfs构建Trie树的fail指针,也就是AC自动机
bfs();
// 输入文本串开始进行查询
cin >> s;
printf("%d\n", query(s));
}
return 0;
}
```
### 五、$Q$:为什么没有边时也需要进行赋值呢,我看原始版本没有这样的代码啊?
**答**:其实$AC$自动机就是一个$Trie+Fail$数组构建的过程,$bfs$由上到下去构建,还想不用$while$循环防止每次都向上查询,就想着从上到下时把信息都填充完整,这样下面用时就不用担心了,(线性$DP$的思路啊~),也就是在第$i$个节点填充$ne[i]$时,它前面的$i-1$都得是已经填充完整的状态,否则无法实现转移。
那如果现在$p$不存在,那就啥不做的话,如果后续节点中有问它这个问题,想找是不是以$p$出发有边$i$时,它可以说没有,人家问那我继续找谁问啊,他说我也不知道,供应链条就断开了,这肯定不行。
那怎么办呢?还得在由上到下的填充过程中想办法,使得就算是不存在的位置,也需要需要退回到哪里去!
退到哪里去呢?就是从当前的视角看,就是退回到离它最近的血缘关系最近的那个节点,也就是有最长公共前后缀的节点吧~,我只能转给它来回答,至它有没有知道不知道,那是它的问题!这是采用的办法就是 李代桃僵!直接将此位置的节点号写成上面血亲的号吧!有人问时,直接就不找我了,直接找它了,呵呵,爽!但它血亲也是这么想的,也可能没有i这条边,所以,它也是抄的上面传递过的值,这样,一个抄一个,问到不知道的,其实就直接没经过它走到了它上$N$级血亲有$i$边的节点上去了,当然,也可能跳到了根。


