'commit'

TangDou/AcWing_TiGao/T3/Floyd/344.cpp

@@ -34,16 +34,8 @@ int main() {
     // 把原始地图复制出来到生成最短距离dis
     memcpy(dis, g, sizeof dis);
 
-    for (int k = 1; k <= n; k++) { // 枚举每一个引入点k来连接缩短i,j的距离
-        /*
-        Q1:为什么循环的时候i和j都需要小于k?
-        A:为了避免经过相同的点，比如i == k时，三个点就变成两个点了。
-        其实循环到n也是可以的，不过当i, j, k中有两个相同时就要continue一下
-
-        Q2:为什么非得把DP的这段代码嵌入到Floyd的整体代码中，不能先Floyd后再进行DP吗？
-        A:是不可以的。因为在进行插入节点号为k时，其实dis[i][j]中记录的是1~k-1插点后的最小距离，
-        而不是全部插入点后的最短距离。
-        */
+    for (int k = 1; k <= n; k++) {
+        // DP
         for (int i = 1; i < k; i++)
             for (int j = i + 1; j < k; j++)
                 if (g[i][k] + g[k][j] < ans - dis[i][j]) { // 减法防止爆INT

TangDou/AcWing_TiGao/T3/Floyd/344.md

@@ -37,33 +37,52 @@ $1≤N≤100,1≤M≤10000,1≤l<500$
 
 ### 二、算法思路
 
+> 环上的节点不重复，并且环上的边的长度之和最小。
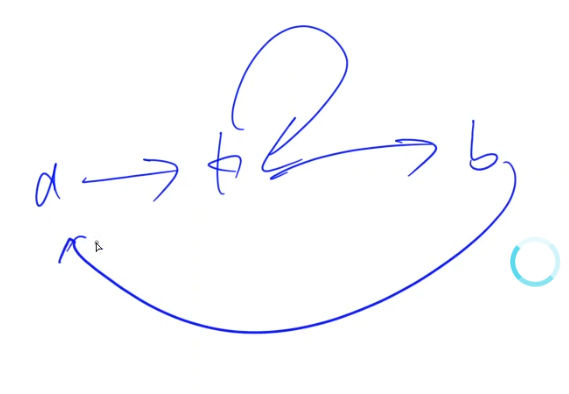
+**解释**：
 ![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401031636536.png)
+> 如果存在一个环，则上图中$k$出现多次，那么，如果去掉$k$身上的那个环，$a \rightarrow k \rightarrow b \rightarrow a $这个环的长度肯定是最小的。
 
 最优化问题，可以从集合角度来思考，从集合角度来思考的一个好处就是：不容易丢东西。
 
 ![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401031639098.png)
 
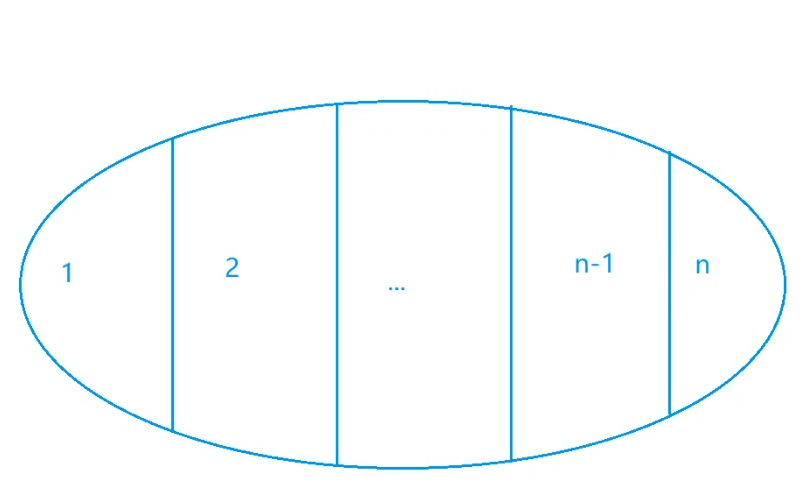
-按环上编号最大点的编号为分类依据，分完类之后，只需要分别求一个每一类的最小值，然后$PK$一下求$min$所有最小值就是答案。
+按 **环上编号最大点的编号** 为分类依据，分完类之后，只需要分别求一个每一类的最小值，然后求$min$所有最小值就是答案。
 
-每一类的最小值怎么求呢？我们来加快一下$floyd$的过程：
+每一类的最小值怎么求呢？我们来回顾一下$floyd$的过程：
 
 ```cpp {.line-numbers}
 for(int k=1;k<=n;k++) //K是要插入的点,dis[i][j]数组相当是知道了i~j的只经过1~k-1这些点的最小路径
     //此时在这个地方可以求第k类。从某个点连接到k
   for(int i=1;i<=n;i++) 
     for(int j=1;j<=n;j++){
-
+        ...
     }
 ```
 ![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401031648374.png)
 
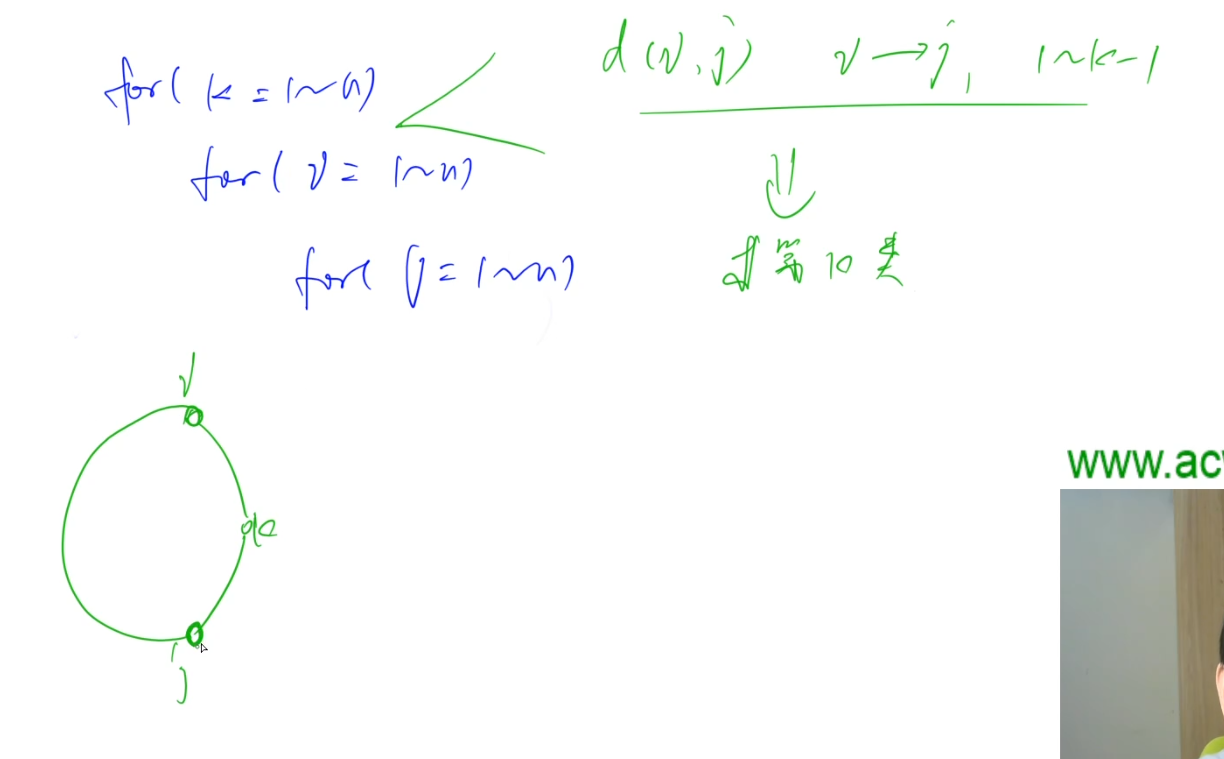
-枚举一下所有的点对(i,j),固定了(i,j)之后，那么$i-k$,$k-j$的长度都是固定的。
+枚举一下所有的点对$(i,j)$,固定了$(i,j)$之后，那么$i \rightarrow k$,$k \rightarrow j$的长度都是固定的。
+而左边那个弧的长度，就是$i \rightarrow j$在只有$1 \sim k-1$号点帮助下可以取得的最短距离，而这个距离恰好被保存在 **当前** 的$dis[i][j]$中。
+
+也就是说，在正常进行$floyd$算法的第一层
+```cpp {.line-numbers}
+for (int k = 1; k <= n ; k++){
+    //这里需要加上一些DP的动作，利用floyd进行dp转移
+     for (int i = 1; i < k; i++)
+            for (int j = i + 1; j < k; j++)
+                if (g[i][k] + g[k][j] < ans - dis[i][j])  // 减法防止爆INT
+                    ans = dis[i][j] + g[i][k] + g[k][j];
+
+    for (int i = 1; i <= n; i++)
+      for (int j = 1;j <=n; j++){
+        ....
+      }
+}
+```
 
 ![](https://dsideal.obs.cn-north-1.myhuaweicloud.com/HuangHai/BlogImages/202401031650078.png)
 
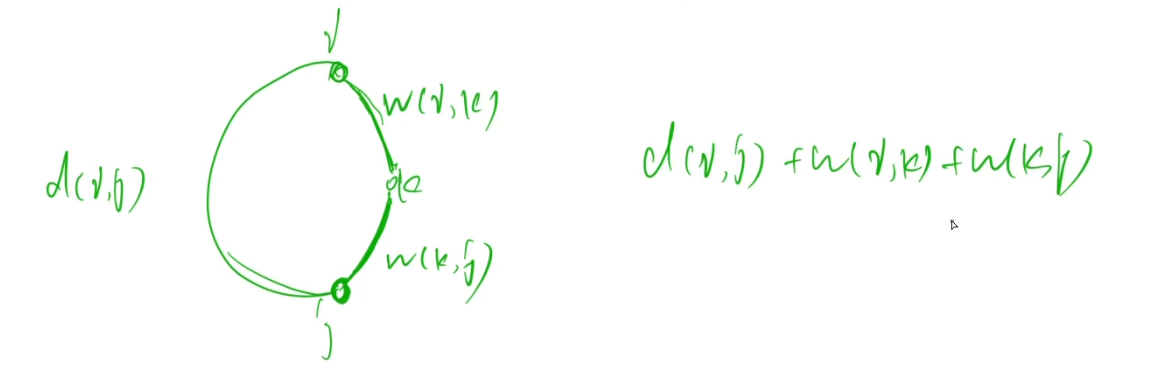
 本题还有一个难点，就是$floyd$需要记录方案，其实就是求一下$d[i][j]$是由哪个中间点转移过来的。
-
-k的含义：不算i,j的情况下，中间点里的最大值。
+****
 
 #### $Code$
 ```cpp {.line-numbers}